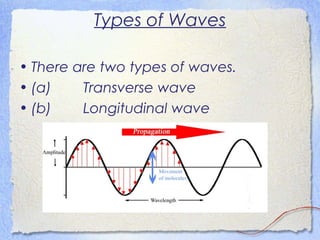
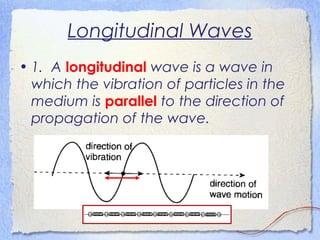
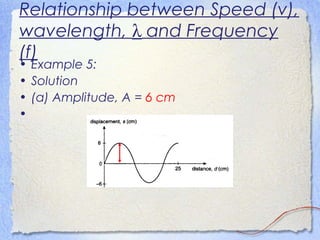
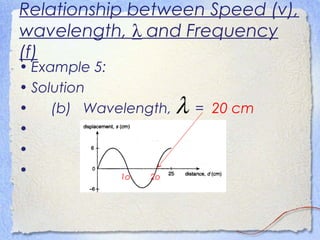
1. Waves transfer energy from one place to another through a medium without transferring matter. They are produced by a vibrating or oscillating source and can be transverse or longitudinal. 2. Key wave properties include amplitude, wavelength, period, frequency, and speed. Amplitude is the maximum displacement from equilibrium, wavelength is the distance between peaks, period is time for one cycle, frequency is cycles per second, and speed depends on wavelength and frequency. 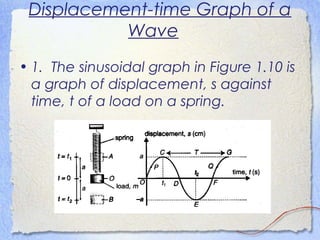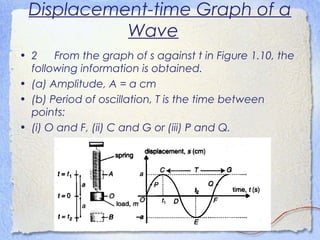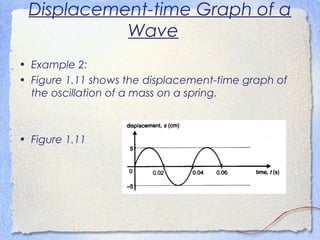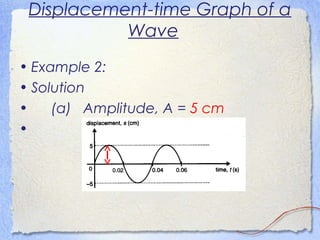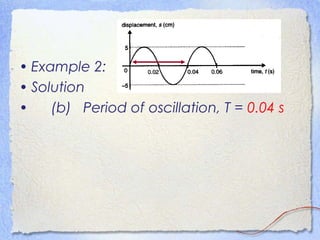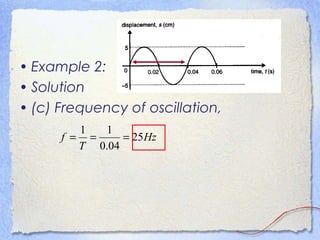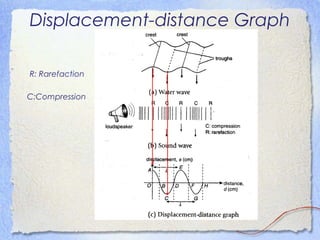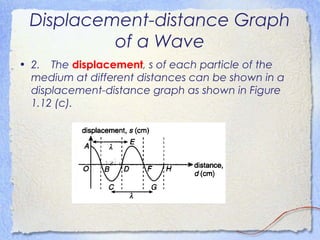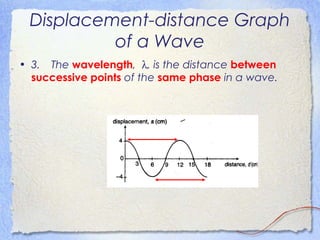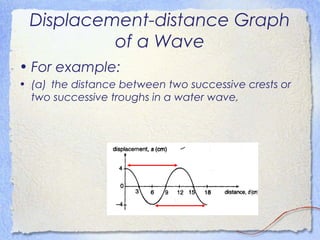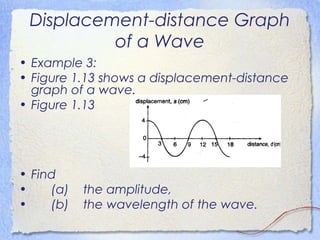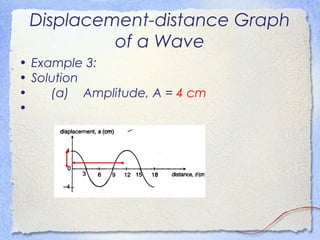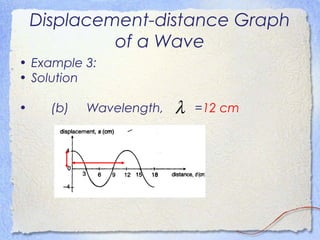3. Waves can be characterized by displacement-time graphs showing oscillation over time or displacement-distance graphs showing the pattern of compression and rarefaction as the wave propagates through a medium.

1. Chapter 1: Waves
1.1 Understanding Waves

2. Motion of Waves
• 1 An oscillating or vibrating motion in
which a point or body moves back and
forth along a line about a fixed central point
produces waves.

3. Motion of Waves
• 2. Examples of waves:
• (a) Light waves are produced as a
result of vibrations of electrons in an
atom.

4. Motion of Waves
• 2. Examples of waves:
• (b)Sound waves are produced by
vibrating mechanical bodies such as
guitar strings or a tuning fork.

5. Motion of Waves
• 2. Examples of waves:
• (c) Water waves are produced by
disturbance (or vibration) on a still
water surface.

6. Propagation (Traveling) of
Waves
• 1.When a wave travels through a
medium, the particles of the medium
vibrate about their equilibrium
positions.
Direction of
waves

7. Propagation (Traveling) of
Waves
• 2.However, the particles of the
medium do not travel in the direction
of the wave.

8. Propagation (Traveling) of
Waves
• 3 A wave transfers energy and the
momentum from the source of the
wave (the oscillating or vibrating
system) to the surroundings.

9. Propagation (Traveling) of
Waves
• Activity 1.1: To demonstrate that waves transfer
energy without transferring matter
• Apparatus:
• Radio, candle and matches.

10. Propagation (Traveling) of
Waves
• Activity 1.1: To demonstrate that waves
transfer energy without transferring matter
• Procedure
• 1. A candle is placed about 10 cm from
the speaker of a radio.

11. Propagation (Traveling) of
Waves
• Procedure
• 2. The candle is lit and the movements of
its flame is observed.

12. Propagation (Traveling) of
Waves
• Procedure
• 3. Then, the radio is turned on and the
volume of the sound is gradually increased
until a change in the movement of the
flame becomes noticeable.

13. Propagation (Traveling) of
Waves
• Discussion
• 1. The flame vibrates when the radio is
turned on.

14. Propagation (Traveling) of
Waves
• Discussion
• 2. This observation shows that the
propagation of the sound waves from
the vibration of the cone of the
speaker transfers energy (or
momentum) to the flame and causes
it to vibrate.

15. Propagation (Traveling) of
Waves
• Conclusion
• Waves transfer energy from a
vibrating system without transferring
matter.

16. Wavefronts
• 1. A wave front is a line or plane on
which the vibrations of every points
on it are in phase and are at the
same distance from the source of the
wave.
Same
Phase

18. Wavefronts
• 2 . Points in a wave are in phase if
they vibrate in the same direction
with the same displacement.
Same
displacement

19. Plane Wave fronts
• 1 . Figure 1.3 shows the production of
plane water waves when a wooden
bar vibrates vertically at a constant
frequency on the surface of the water.

20. Plane Wave fronts
• 2. Lines PQ, RS, TU and VW are straight
lines along the respective crests of the
waves. These lines are called wave
fronts.

21. Circular Wave fronts
• 1. When we use a fingertip to touch
the surface of water repeatedly,
circular wave fronts are produced as
shown in Figure 1.4.

22. Types of Waves
• There are two types of waves.
• (a) Transverse wave
• (b) Longitudinal wave

23. Transverse Waves
• 1. A transverse wave is a wave in
which the vibration of particles in the
medium is at right angle
(perpendicular) to the direction of
propagation of the wave.

24. Transverse Waves
• 2. A model of a transverse wave can
be produced by a slinky spring as
shown in Figure 1.6.

25. Transverse Waves
• 3. Examples of transverse waves are
water waves and light waves.

26. Longitudinal Waves
• 1. A longitudinal wave is a wave in
which the vibration of particles in the
medium is parallel to the direction of
propagation of the wave.

27. Longitudinal Waves
• 2. When the slinky spring is vibrated
back and forth along the direction of
propagation of the wave at a fixed
rate, a longitudinal wave is produced
as shown in Figure 1.8.

28. Longitudinal Waves
• 3 . Example of longitudinal waves is
sound waves.

29. Amplitude, Period and Frequency of a
Wave
• 1 . The amplitude, A, of a vibrating system is
maximum displacement from its equilibrium
position. It is a measure of height of the wave crest
or depth of the wave trough.
Amplitude

30. Amplitude, Period and Frequency of a
Wave
• 2 . In Figures 1.9 (a) and (b), the distance OQ is the
amplitude, where O is the equilibrium position of the
vibrating system.
Amplitude

31. Amplitude, Period and Frequency of a
Wave
• 3 . The period, T, of a vibrating system is the time
taken to complete an oscillation.
Period

32. Amplitude, Period and Frequency of a
Wave
• 4. In the two vibrating (oscillating) systems show in
Figure 1.9, a complete oscillation are:
• (a) from P  Q  P or Q  P Q,
• (b) from OPQO or
OQPO

33. Amplitude, Period and Frequency of a
Wave
• 5. If a vibrating system makes n
complete oscillations in a time of t
seconds, the period of oscillation, T of
the system is second
• The SI unit of period is second.
n
t

34. Amplitude, Period and
Frequency of a Wave
• 6 The frequency, f, is the number of complete
oscillations made by a vibrating system in one
second.
• The unit of frequency is hertz (Hz) or s-1
.

35. Amplitude, Period and
Frequency of a Wave
• 7 From the formulae of T and f, the relationship
between period, T and frequency, f is:
• T is inversely proportional to f and vice versa.

36. Amplitude, Period and
Frequency of a Wave
• Example 1:
• In an experiment, Aziz observes that a simple
pendulum completes 30 oscillations in 48.0 seconds.
What is
• (a) the period of oscillation?
• (b) the frequency of oscillation?

37. Amplitude, Period and
Frequency of a Wave
• Example 1:
• Solution
• (a)
s6.1
30
48.0
oscllationcompletedofnumber
takentime
Tperiod,
==
=

38. Amplitude, Period and
Frequency of a Wave
• Example 1:
• Solution
• (b)
Hz625.0
6.1
1
T
1
ffrequency, ===

39. Displacement-time Graph of a
Wave
• 1. The sinusoidal graph in Figure 1.10 is
a graph of displacement, s against
time, t of a load on a spring.

40. Displacement-time Graph of a
Wave
• 2 From the graph of s against t in Figure 1.10, the
following information is obtained.
• (a) Amplitude, A = a cm
• (b) Period of oscillation, T is the time between
points:
• (i) O and F, (ii) C and G or (iii) P and Q.

41. Displacement-time Graph of a
Wave
• Example 2:
• Figure 1.11 shows the displacement-time graph of
the oscillation of a mass on a spring.
• Figure 1.11

42. Displacement-time Graph of a
Wave
• Example 2:
• From the graph,
• (a) state the amplitude,
• (b) calculate the period of the oscillation,
• (c) calculate the frequency of the oscillation.

43. Displacement-time Graph of a
Wave
• Example 2:
• Solution
• (a) Amplitude, A = 5 cm
•

44. • Example 2:
• Solution
• (b) Period of oscillation, T = 0.04 s

45. • Example 2:
• Solution
• (c) Frequency of oscillation,
Hz
T
f 25
04.0
11
===

46. Displacement-distance Graph
of a Wave
• 1. Figures 1.12 (a) and (b) show the
propagation of a water wave and a
sound wave.

47. Displacement-distance Graph
of a Wave
R: Rarefaction
C:Compression

48. Displacement-distance Graph
of a Wave
• 2. The displacement, s of each particle of the
medium at different distances can be shown in a
displacement-distance graph as shown in Figure
1.12 (c).

49. Displacement-distance Graph
of a Wave
• 3. The wavelength, λ, is the distance between
successive points of the same phase in a wave.

50. Displacement-distance Graph
of a Wave
• For example:
• (a) the distance between two successive crests or
two successive troughs in a water wave,

51. Displacement-distance Graph
of a Wave
• (b) the distance between two successive
compressions or two successive rarefactions in a
sound wave.
The SI unit of wavelength, λ , is metre (m).

52. Displacement-distance Graph
of a Wave
• Example 3:
• Figure 1.13 shows a displacement-distance
graph of a wave.
• Figure 1.13
• Find
• (a) the amplitude,
• (b) the wavelength of the wave.

53. Displacement-distance Graph
of a Wave
• Example 3:
• Solution
• (a) Amplitude, A = 4 cm
•

54. Displacement-distance Graph
of a Wave
• Example 3:
• Solution
• (b) Wavelength, =12 cmλ

55. Relationship between Speed (v),
wavelength, λ and Frequency (f)
• The relationship between speed,
wavelength and frequency can be
obtained by relating the SI unit of the
quantities.
λfv =

56. Relationship between Speed (v),
wavelength, λ and Frequency (f)
• Example 4:
• A wave of frequency 120 Hz has a
wavelength of 5.0 m. What is the
speed of the wave?

57. Relationship between Speed (v),
wavelength, λ and Frequency (f)
• Example 4:
• A wave of frequency 120 Hz has a
wavelength of 5.0 m. What is the
speed of the wave?
Solution
f = 120 Hz and λ =5.0m
Speed of wave,
v = f λ
= 120 x 5
= 600 m s-1

58. Relationship between Speed (v),
wavelength, λ and Frequency (f)
• Example 5:
• The displacement-distance graph in
Figure 1.14 shows the motion of a
transverse wave. The source of the
wave produces 10 complete waves in
one second.
• Figure 1.14

59. Relationship between Speed (v), wavelength,
λ and Frequency (f)
• Example 5:
• Calculate
• (a) the amplitude,
• (b) the wavelength, and
• (c) the speed of the wave.

60. Relationship between Speed (v),
wavelength, λ and Frequency
(f)
• Example 5:
• Solution
• (a) Amplitude, A = 6 cm
•

61. Relationship between Speed (v),
wavelength, λ and Frequency
(f)
• Example 5:
• Solution
• (b) Wavelength, = 20 cm
•
•
•
λ
1o 2o

62. Relationship between Speed (v),
wavelength, λ and Frequency
(f)
• Example 5:
• Solution
• (c) Frequency, f = 10 Hz, = 20 cm
• Speed, v = f
=10x20
• = 200 cm s-1
λ
λ