智出
Uploaded by智啓 出川
PDF, PPTX2,381 views

2015年度GPGPU実践プログラミング　第12回　偏微分方程式の差分計算

長岡技術科学大学 2015年度GPGPU実践プログラミング（全15回，学部4年対象講義） 第12回偏微分方程式の差分計算 2015年度GPGPU実践プログラミング ・第1回　GPGPUの歴史と応用例 http://www.slideshare.net/ssuserf87701/2015gpgpu1-59179080 ・第2回　GPUのアーキテクチャとプログラム構造 http://www.slideshare.net/ssuserf87701/2015gpgpu2-59179215 ・第3回　GPGPUプログラミング環境 http://www.slideshare.net/ssuserf87701/2015gpgpu3-59179255 ・第3回補足 GROUSEの利用方法 http://www.slideshare.net/ssuserf87701/2015gpgpu3-59183677 ・第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法） http://www.slideshare.net/ssuserf87701/2015gpgpu4-59179449 ・第5回　GPUのメモリ階層 http://www.slideshare.net/ssuserf87701/2015gpgpu5-59179536 ・第6回　パフォーマンス解析ツール http://www.slideshare.net/ssuserf87701/2015gpgpu6-59179577 ・第7回　総和計算 http://www.slideshare.net/ssuserf87701/2015gpgpu7-59179639 ・第8回　総和計算（高度な最適化） http://www.slideshare.net/ssuserf87701/2015gpgpu8-59179686 ・第9回　行列計算（行列－行列積） http://www.slideshare.net/ssuserf87701/2015gpgpu9-59179722 ・第10回　行列計算（行列－行列積の高度な最適化） http://www.slideshare.net/ssuserf87701/2015gpgpu10-59179759 ・第11回　画像処理 http://www.slideshare.net/ssuserf87701/2015gpgpu11-59179789 ・第12回　偏微分方程式の差分計算 http://www.slideshare.net/ssuserf87701/2015gpgpu12-59179972 ・第13回　多粒子の運動 http://www.slideshare.net/ssuserf87701/2015gpgpu13-59180018 ・第14回　N体問題 http://www.slideshare.net/ssuserf87701/2015gpgpu14-59180054 ・第15回　GPU最適化ライブラリ http://www.slideshare.net/ssuserf87701/2015gpgpu15-59180086 2015年度先端GPGPUシミュレーション工学特論 ・第1回　先端シミュレーションおよび産業界におけるGPUの役割 http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180313 2015年度GPGPU実践基礎工学 ・第1回　学際的分野における先端シミュレーション技術の歴史 http://www.slideshare.net/ssuserf87701/2015gpgpu1 講義には長岡技術科学大学のGPGPUシステム（GROUSE）を利用しています。 開発環境 CPU　Intel Xeon X5670 × 32 GPU　NVIDIA Tesla M2050（Fermi世代） × 64 CUDA 4.0（諸般の事情によりバージョンアップされていません） PGI Fortran 11.3

Embed presentation

Download as PDF, PPTX
第12回 偏微分方程式の差分計算 長岡技術科学大学 電気電子情報工学専攻 出川智啓
今回の内容 2015/07/01GPGPU実践プログラミング2  差分法  1階微分，2階微分に対する差分法  2次元拡散方程式  gnuplotによる結果の表示  if分岐の書き方による実行時間の変化  高速化に利用できるいくつかのテクニック
前回授業 2015/07/01GPGPU実践プログラミング3  ビットマップを使った画像処理  配列の1要素が物理的な配置に対応  配列の1要素に物理的なデータが定義 B G R
数値計算（差分法） 2015/07/01GPGPU実践プログラミング4  計算機を利用して数学・物理学的問題の解を計算  微積分を計算機で扱える形に変換  差分法では微分を差分に置き換え  処理自体は単純  精度を上げるために計算量が増加
シミュレーションの歴史と進歩  自動車シミュレーションにおける例  姫野龍太郎，次世代スーパーコンピュータとは そして，何がで きるようになるか  http://accc.riken.jp/wp‐content/uploads/2015/06/secur e_4650_20100507kobe.pdf  スライド6, 8  1985年  2次元でのシミュレーション  実験結果と“傾向は”一致  1987年  3次元化し，実車に近い形状で計算 2015/07/01GPGPU実践プログラミング5
シミュレーションの歴史と進歩  自動車シミュレーションにおける例  1988年～1990年  車輪や床下も含めたモデル化  1993年  空気抵抗を誤差1%で予測可能  空力解析以外にも利用  1992年～1993年  車体から発生する騒音のシミュレーション  ドアミラーやピラーの形状の改良  エンジンルームの冷却  10mm以上の部品は全て含めて解析 2015/07/01GPGPU実践プログラミング6
数値計算（差分法） 2015/07/01GPGPU実践プログラミング8  物理空間に観測点を設置  観測点での物理量の変化を計算  観測点群を配列として確保し，その点で物理量を定義 観測点 （固定）  画像処理に類似  画素が観測点に相当  画素を配列として確保  画素の値を変化させることで 画像処理を実現
偏微分方程式（拡散方程式）  物質の拡散を表す方程式  水の中に落ちたインクの拡散，金属中の熱伝導等  時刻t=0におけるfの分布（初期値）が既知  時間進行に伴い，fがどのように変化するかを計算  時間積分しながらfの分布を求める 2 2 ),(),( x txf t txf      GPGPU実践プログラミング9 2015/07/01 2 2 2 2 ),,(),,(),,( y tyxf x tyxf t tyxf        
差分法 2015/07/01GPGPU実践プログラミング10  計算機で微分を計算する方法の一つ  微分の定義  xの関数fについて，xだけ離れた2点間の傾きを計算し，2点の間隔を 無限小に近づけたときの極限  差分近似  関数をある間隔でサンプリング  その間隔xがfの変化に対して十分小さいと仮定 Δx xfΔxxf dx df Δx )()( lim 0    Δx xfΔxxf dx df )()(  
差分法（理論的なお話） 2015/07/01GPGPU実践プログラミング11  差分の誤差  limを排除したことでどの程度の誤差が入るのか  関数fのテイラー展開を利用 Δx xfΔxxf Δx xfΔxxf dx df Δx )()()()( lim 0       3 33 2 22 !3!2 )()( dx fdΔx dx fdΔx dx df ΔxxfΔxxf          3 33 2 22 !3!2 1)()( dx fdΔx dx fdΔx ΔxΔx xfΔxxf dx df
差分法（理論的なお話）  空間打ち切り誤差  定義とテイラー展開の比較  テイラー展開を有限項で打ち切ったことによる誤差          3 33 2 22 !3!2 1)()( dx fdΔx dx fdΔx ΔxΔx xfΔxxf dx df Δx xfΔxxf Δx xfΔxxf dx df Δx )()()()( lim 0      誤差        3 32 2 2 !3!2 dx fdΔx dx fdΔx GPGPU実践プログラミング12 2015/07/01
2階微分の離散化  テイラー展開を応用  x方向にx離れた2点で展開  2式を足すと1階微分が消滅           3 33 2 22 !3!2 )()( x fΔx x fΔx x f ΔxxfΔxxf           3 33 2 22 !3!2 )()( x fΔx x fΔx x f ΔxxfΔxxf     2 22 !2 2)(2)()( x fΔx xfΔxxfΔxxf GPGPU実践プログラミング13 2015/07/01
2階微分の離散化  2階微分の式に整理 22 2 )()(2)( Δx ΔxxfxfΔxxf x f     GPGPU実践プログラミング14 2015/07/01 x f(x) f(x−x) f(x) x x=0 ･･･ x−x x x+x f(x+x)
2階微分の離散化  2階微分の式に整理 22 2 )()(2)( Δx ΔxxfxfΔxxf x f     GPGPU実践プログラミング15 2015/07/01 dx サンプリングされた関数値 を配列f[]で保持 f[i] f[i‐1] f[i+1] 2階の中心差分 (f[i+1]‐2*f[i]+f[i‐1])/(dx*dx) f[i] i i=0 ･･･ i−1 i i+1
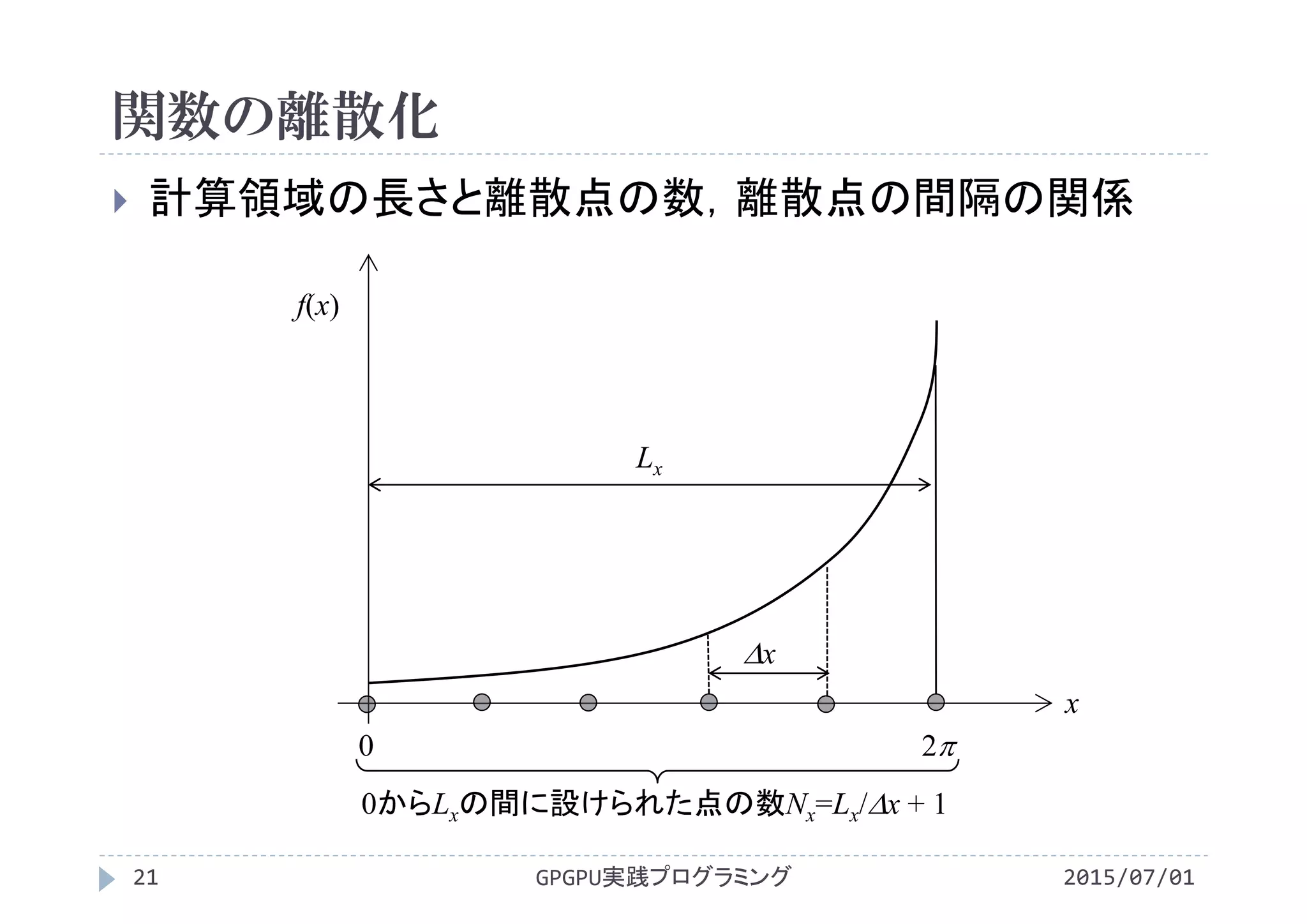
2階微分の離散化 2015/07/01GPGPU実践プログラミング16  サンプリングされた関数値fの保持  x方向長さ（計算領域の長さ）を等間隔xに分割  間隔xの両端に離散点（観測点）を置き，そこでfの値を定義  原点から順に離散点に番号を付与し，iで表現  離散点iにおけるfの値を配列f[i]に保存 配列f[] i=0   ･･･ i−1  i i+1 f[i] i 離散点 配列（メモリ）
差分法の実装 2015/07/01GPGPU実践プログラミング17  計算領域内部  d2fdx2[i]=(f[i‐1]‐2*f[i]+f[i+1])/dxdx;  境界条件(関数値が無いため処理を変更)  d2fdx2[0  ]=(2*f[0  ]‐5*f[1  ]+4*f[2  ]‐f[3  ])/dxdx;  d2fdx2[N‐1]=(2*f[N‐1]‐5*f[N‐2]+4*f[N‐3]‐f[N‐4])/dxdx; d2fdx2[i] f[i] ＋ ＋ ＋ ＋ ＋ 2 1 Δx ＋
差分法の実装 2015/07/01GPGPU実践プログラミング18  計算領域内部  d2fdx2[i]=(f[i‐1]‐2*f[i]+f[i+1])/dxdx;  境界条件(関数値が無いため処理を変更)  d2fdx2[0  ]=(2*f[0  ]‐5*f[1  ]+4*f[2  ]‐f[3  ])/dxdx;  d2fdx2[N‐1]=(2*f[N‐1]‐5*f[N‐2]+4*f[N‐3]‐f[N‐4])/dxdx; d2fdx2[i] f[i] ＋ 2 1 Δx
差分法の実装 2015/07/01GPGPU実践プログラミング19  計算領域内部  d2fdx2[i]=(f[i‐1]‐2*f[i]+f[i+1])/dxdx;  境界条件(関数値が無いため処理を変更)  d2fdx2[0  ]=(2*f[0  ]‐5*f[1  ]+4*f[2  ]‐f[3  ])/dxdx;  d2fdx2[N‐1]=(2*f[N‐1]‐5*f[N‐2]+4*f[N‐3]‐f[N‐4])/dxdx; d2fdx2[i] f[i] 2 1 Δx ＋
#include<stdlib.h> #include<math.h>/*‐lmオプションが必要*/ #define Lx (2.0*M_PI) #define Nx (256) #define dx (Lx/(Nx‐1)) #define Nbytes (Nx*sizeof(double)) #define dxdx (dx*dx) void init(double *f){ int i; for(i=0; i<Nx; i++){ f[i] = sin(i*dx); } } void differentiate(double *f, double *d2fdx2){ int i; d2fdx2[0] = ( 2.0*f[0] ‐5.0*f[1] +4.0*f[2] ‐ f[3])/dxdx; for(i=1; i<Nx‐1; i++) d2fdx2[i] = (     f[i+1] ‐2.0*f[i ] +    f[i‐1])/dxdx; d2fdx2[Nx‐1]=(‐ f[Nx‐4] +4.0*f[Nx‐3] ‐5.0*f[Nx‐2] +2.0*f[Nx‐1])/dxdx; } int main(void){ double *f,*d2fdx2; f      = (double *)malloc(Nbytes); d2fdx2 = (double *)malloc(Nbytes); init(f); differentiate(f,d2fdx2); return 0; } 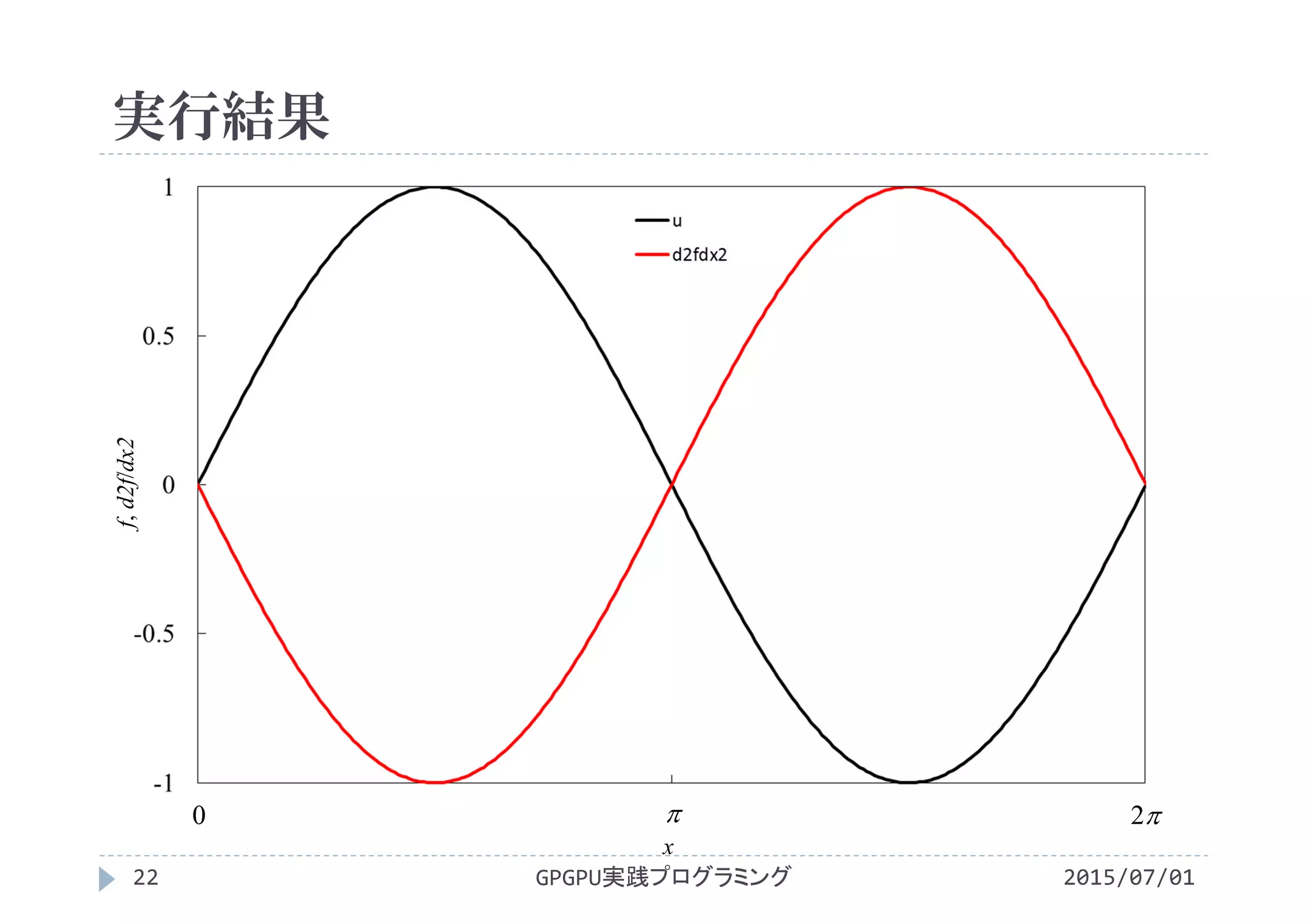CPUプログラム 2015/07/01GPGPU実践プログラミング20 differentiate.c
関数の離散化 2015/07/01GPGPU実践プログラミング21  計算領域の長さと離散点の数，離散点の間隔の関係 f(x) x x 0 2 Lx 0からLxの間に設けられた点の数Nx=Lx/x + 1
実行結果 2015/07/01GPGPU実践プログラミング22   x f,d2f/dx2
GPUへの移植  計算領域内部を計算するスレッド  d2fdx2[i]=(f[i‐1]‐2*f[i]+f[i+1])/dxdx;  境界を計算するスレッド  d2fdx2[0  ]=(2*f[0  ]‐5*f[1  ]+4*f[2  ]‐f[3  ])/dxdx;  d2fdx2[N‐1]=(2*f[N‐1]‐5*f[N‐2]+4*f[N‐3]‐f[N‐4])/dxdx; 2015/07/01GPGPU実践プログラミング23 d2fdx2[i] f[i] ＋ ＋ ＋ ＋ ＋ ＋ 2 1 Δx ＋ ＋
#include<stdio.h> #include<stdlib.h> #include<math.h>/*‐lmオプションが必要*/ #define Lx (2.0*M_PI) #define Nx (256) #define dx (Lx/(Nx‐1)) #define Nbytes (Nx*sizeof(double)) #define dxdx (dx*dx) #define NT      (128) #define NB      (Nx/NT) void init(double *f){ int i; for(i=0; i<Nx; i++){ f[i] = sin(i*dx); } } __global__ void differentiate (double *f, double *d2fdx2){ int i = blockIdx.x*blockDim.x + threadIdx.x; if(i==0) d2fdx2[i] = ( 2.0*f[i ] ‐5.0*f[i+1] +4.0*f[i+2] ‐ f[i+3])/dxdx; if(0<i && i<Nx‐1) d2fdx2[i] = (     f[i+1] ‐2.0*f[i ] +    f[i‐1])/dxdx; if(i==Nx‐1) d2fdx2[i]=(‐ f[i‐3] +4.0*f[i‐2] ‐5.0*f[i‐1] +2.0*f[i ])/dxdx; } GPUプログラム 2015/07/01GPGPU実践プログラミング24 differentiate.cu
int main(void){ double *host_f,*host_d2fdx2; double *f,*d2fdx2; host_f =(double *)malloc(Nbytes); cudaMalloc((void **)&f,Nbytes); cudaMalloc((void **)&d2fdx2,Nbytes); init(host_f); cudaMemcpy(f, host_f, Nbytes, cudaMemcpyHostToDevice); differentiate<<<NB, NT>>>(f, d2fdx2); //host_d2fdx2=(double *)malloc(Nbytes); //cudaMemcpy(host_d2fdx2, d2fdx2, Nbytes, cudaMemcpyDeviceToHost); //for(int i=0; i<Nx; i++)printf("%f,%f,%f¥n",i*dx,host_f[i],host_d2fdx2[i]); free(host_f); free(host_d2fdx2); cudaFree(f); cudaFree(d2fdx2); return 0; } GPUプログラム 2015/07/01GPGPU実践プログラミング25 differentiate.cu
2次元への拡張 2015/07/01GPGPU実践プログラミング26  拡散方程式  1次元  2次元 2 2 ),(),( x txf t txf      2 2 2 2 ),,(),,(),,( y tyxf x tyxf t tyxf         differentiate.cuで計算 どのように2次元 に拡張するか どのように離散化 するか
2次元への拡張  x方向2階偏微分  y方向を固定してx方向に偏微分  y方向2階偏微分  x方向を固定してy方向に偏微分 22 2 ),(),(2),( Δx yΔxxfyxfyΔxxf x f     22 2 ),(),(2),( Δy ΔyyxfyxfΔyyxf y f     GPGPU実践プログラミング27 2015/07/01
時間積分  時間微分項の離散化  時間微分項を前進差分で離散化  右辺のt+tの項を移行 Δt tyxfΔttyxf t f ),,(),,(     GPGPU実践プログラミング28 2015/07/01 f t f 2    t f ΔttyxfΔttyxf    ),,(),,( 拡散方程式を代入 ),,(),,(),,( 2 tyxfΔttyxfΔttyxf  f(x, y, t)の2階微分を計算できればf(x, y, t+t)が求められる
離散化された方程式の記述  簡略化した表現  配列との対応をとるため下付き添字i, jを利用  時間は，上付き添字nを利用 jifyxf ,),(  jifyΔxxf ,1),(  1,),(  jifΔyyxf n jiftyxf ,),,(  1 ,),,(   n jifΔttyxf GPGPU実践プログラミング29 2015/07/01
離散化された拡散方程式  連続系  離散系  t秒後の値 2 2 2 2 ),,(),,(),,( y tyxf x tyxf t tyxf         2 1,,1, 2 ,1,,1, 1 , 22 Δy fff Δx fff Δt ff n ji n ji n ji n ji n ji n ji n ji n ji                     2 1,,1, 2 ,1,,1 , 1 , 22 Δy fff Δx fff Δtff n ji n ji n ji n ji n ji n jin ji n ji GPGPU実践プログラミング30 2015/07/01
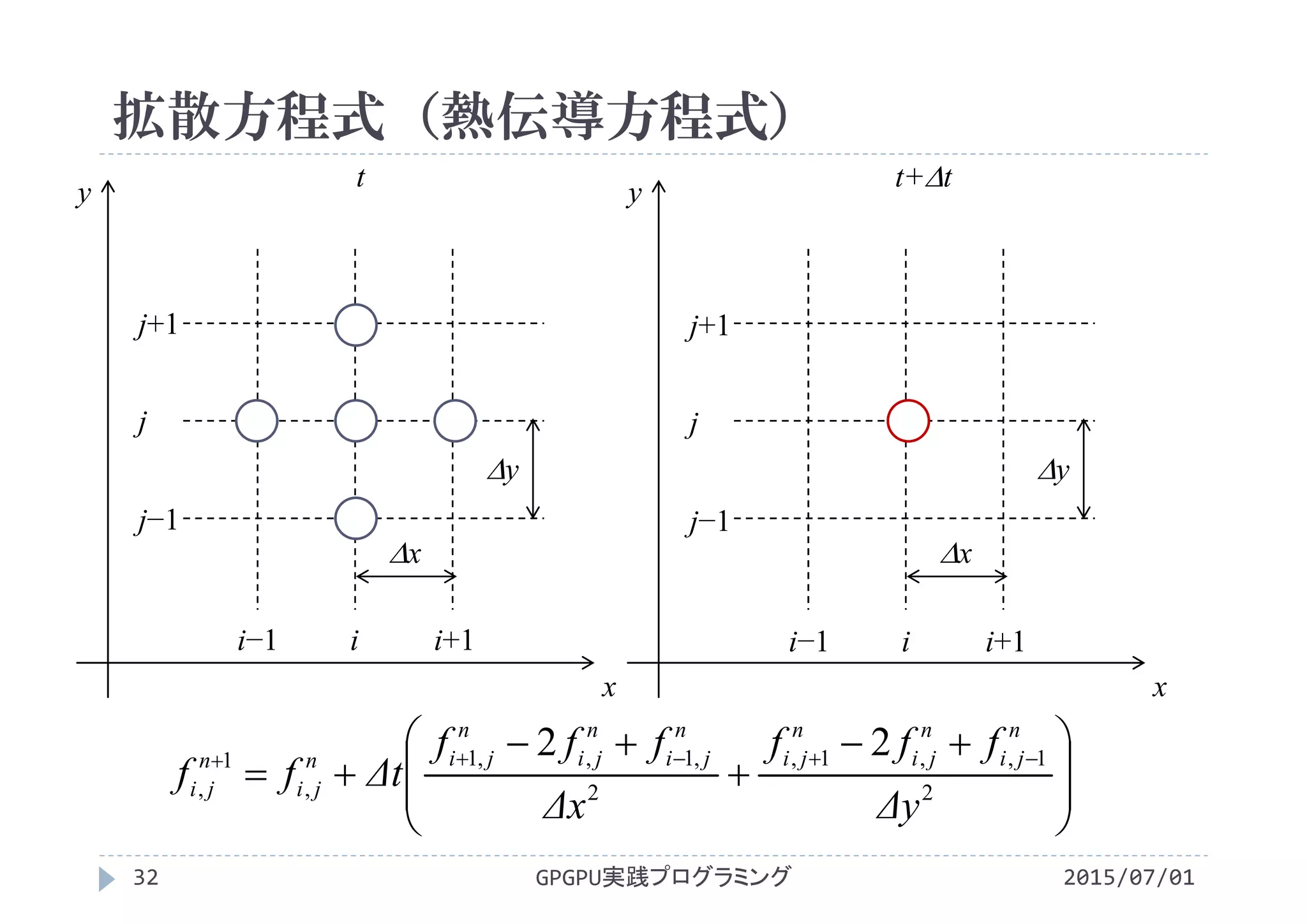
離散化された関数値の保持 2015/07/01GPGPU実践プログラミング31  各方向を等間隔x, yに分割し，離散点を配置  離散点で関数値を定義し，配列に保存 配列f[][] i=0   ･･･ i−1  i i+1 i 離散点 配列（メモリ） j=0   ･･･j−1 j  j+1
拡散方程式（熱伝導方程式） x y i i+1i−1 j j+1 j−1 x y x y x y t t+t GPGPU実践プログラミング32 2015/07/01              2 1,,1, 2 ,1,,1 , 1 , 22 Δy fff Δx fff Δtff n ji n ji n ji n ji n ji n jin ji n ji i i+1i−1 j j+1 j−1
拡散方程式の安定性 2015/07/01GPGPU実践プログラミング33  プログラムを正しく作成しても正常な計算結果が得られ ない場合がある  安定条件  拡散の強さを表す係数（拡散係数）を使った形  二つの条件を満たすことが必要条件（結果が正しいかは別） 5.02  Δx Δt v 5.02  Δy Δt v              2 1,,1, 2 ,1,,1 , 1 , 22 Δy fff Δx fff Δtff n ji n ji n ji n ji n ji n jin ji n ji 
計算手順 1. 計算条件の決定  計算領域の大きさLx, Ly  計算領域の分割数（離散点の個数）Nx, Ny  離散点同士の間隔（格子間隔）x, y  計算時間間隔t 2. 初期値の決定  fの初期分布の決定 3. 差分値の計算  fの分布からx, y方向の2階微分値を計算  境界条件に基づいて境界の値を決定  t秒後のfを計算 GPGPU実践プログラミング34 2015/07/01
CPUプログラム  計算条件の決定  計算領域の大きさLx, Ly  計算領域の分割数 （離散点の個数）Nx, Ny  離散点同士の間隔 （格子間隔）x, y  計算時間間隔t #include<stdio.h> #include<stdlib.h> #include<math.h> #define Lx (1.0) #define Ly (1.0) #define Nx 128 #define Ny 128 #define dx (Lx/(Nx‐1)) #define dy (Ly/(Ny‐1)) #define dt 0.0001 GPGPU実践プログラミング35 2015/07/01
CPUプログラム  初期条件  境界条件 GPGPU実践プログラミング36 2015/07/01       )2.0(1 )2.0(0 r r f 1 1 x y r 0   n f n n n: 外向き法線ベクトル jiji jiji ff Δx ff ,1,1 ,1,1 0 2     1,1, 1,1, 0 2     jiji jiji ff Δy ff 22 yxr 
#include<stdlib.h> #include<math.h> #define Lx (1.0) #define Ly (1.0) #define Nx 128 #define Ny 128 #define dx (Lx/(Nx‐1)) #define dy (Ly/(Ny‐1)) #define dt 0.0001 #define endT (1.0) #define Nt (int)(endT/dt) #define DIFF (0.01) #define dxdx (dx*dx) #define dydy (dy*dy) #define Nbytes (Nx*Ny*sizeof(double)) void init(double *, double *, double *); void laplacian(double *, double *); void integrate(double *, double *, double *); void update(double *, double *); int main(void){ double *f,*f_new,*f_lap,x,y; int i,j,n; f     = (double *)malloc(Nx*Ny*sizeof(double)); f_new = (double *)malloc(Nx*Ny*sizeof(double)); f_lap = (double *)malloc(Nx*Ny*sizeof(double)); init(f, f_lap, f_new); for(n=0;n<Nt;n++){ laplacian(f,f_lap); integrate(f,f_lap,f_new); update(f,f_new); } return 0; } CPUプログラム 2015/07/01GPGPU実践プログラミング37 diffusion.c
void init(double *f, double *f_lap, double *f_new){ int i,j,ij; double x,y; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ f    [i+Nx*j] = 0.0; f_lap[i+Nx*j] = 0.0; f_new[i+Nx*j] = 0.0; x=i*dx‐Lx/2.0; y=j*dy‐Ly/2.0; if(sqrt(x*x+y*y)<=0.2) f[i+Nx*j] = 1.0; } } } void laplacian(double *f, double *f_lap){ int i,j,ij,ip1j,im1j,ijp1,ijm1; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij =  i+Nx*j; im1j=i‐1+Nx* j;   if(i‐1< 0 )im1j=i+1+Nx*j; ip1j=i+1+Nx* j;   if(i+1>=Nx)ip1j=i‐1+Nx*j; ijm1=i +Nx*(j‐1);if(j‐1< 0 )ijm1=i+Nx*(j+1); ijp1=i +Nx*(j+1);if(j+1>=Ny)ijp1=i+Nx*(j‐1); f_lap[ij] = (f[ip1j]‐2.0*f[ij]+f[im1j])/dxdx +(f[ijp1]‐2.0*f[ij]+f[ijm1])/dydy; } } } void integrate (double *f, double *f_lap, double *f_new){ int i,j,ij; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij =  i+Nx*j; f_new[ij] = f[ij] + dt*DIFF*f_lap[ij]; } } } void update(double *f, double *f_new){ int i,j,ij; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij =  i+Nx*j; f[ij] = f_new[ij]; } } } CPUプログラム 2015/07/01GPGPU実践プログラミング38 diffusion.c
CPUプログラム  差分計算  x方向，y方向偏微分を個別に計算して加算 void laplacian(double *f, double *f_lap){ int i,j,ij,ip1j,im1j,ijp1,ijm1; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij =i +Nx* j; im1j=i‐1+Nx* j;   if(i‐1< 0 )im1j=i+1+Nx*j; ip1j=i+1+Nx* j;   if(i+1>=Nx)ip1j=i‐1+Nx*j; ijm1=i +Nx*(j‐1);if(j‐1< 0 )ijm1=i+Nx*(j+1); ijp1=i +Nx*(j+1);if(j+1>=Ny)ijp1=i+Nx*(j‐1); f_lap[ij] = (f[ip1j]‐2.0*f[ij]+f[im1j])/dxdx +(f[ijp1]‐2.0*f[ij]+f[ijm1])/dydy; } } } GPGPU実践プログラミング39 2015/07/01
ラプラシアン計算のメモリ参照  ある1点i,jのラプラシアンを計算するために，周囲5点 のfを参照 GPGPU実践プログラミング40 2015/07/01 f[] f_lap[] i−1 i i+1 j−1jj+1
ラプラシアン計算のメモリ参照  ある1点i,jのラプラシアンを計算するために，周囲5点 のfを参照 GPGPU実践プログラミング41 2015/07/01 i−1 i i+1 j−1jj+1 f[] f_lap[]
ラプラシアン計算のメモリ参照  ある1点i,jのラプラシアンを計算するために，周囲5点 のfを参照 GPGPU実践プログラミング42 2015/07/01 i−1 i i+1 j−1jj+1 f[] f_lap[]
ラプラシアン計算のメモリ参照  ある1点i,jのラプラシアンを計算するために，周囲5点 のfを参照 GPGPU実践プログラミング43 2015/07/01 i−1 i i+1 j−1jj+1 f[] f_lap[]
ラプラシアン計算のメモリ参照  ある1点i,jのラプラシアンを計算するために，周囲5点 のfを参照  全てのfを参照し，領域内部のf_lapを計算 GPGPU実践プログラミング44 2015/07/01 f[] f_lap[]
CPUプログラム  境界条件  法線方向の1階微分が0  境界での2階の差分式 GPGPU実践プログラミング45 2015/07/01 f_lap[] 0   n f n: 外向き法線ベクトル jiji jiji ff Δx ff ,1,1 ,1,1 0 2     1,1, 1,1, 0 2     jiji jiji ff Δy ff 2 ,,1 2 ,,1 2 ,1,,1 22 or 222 Δx ff Δx ff Δx fff jijijijijijiji     2 ,1, 2 ,1, 2 1,,1, 22 or 222 Δy ff Δy ff Δy fff jijijijijijiji    
CPUプログラム  境界条件  参照する点が境界からはみ出して いる場合は添字を修正  2階微分を計算する式は変更なし  右端ではi+1をi‐1に修正  左端ではi‐1をi+1に修正  上端ではj+1をj‐1に修正  下端ではj‐1をj+1に修正 GPGPU実践プログラミング46 2015/07/01 f_lap[] if(i‐1< 0 )im1j=i+1+Nx*j; if(i+1>=Nx)ip1j=i‐1+Nx*j; if(j‐1< 0 )ijm1=i +Nx*(j+1); if(j+1>=Ny)ijp1=i +Nx*(j‐1);
CPUプログラム  fの積分 void integrate(double *f, double *f_lap, double *f_new){ int i,j,ij; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij = i+Nx*j; f_new[ij] = f[ij] + dt*DIFF*f_lap[ij]; } } } GPGPU実践プログラミング47 2015/07/01              2 1,,1, 2 ,1,,1 , 1 , 22 Δy fff Δx fff Δtff n ji n ji n ji n ji n ji n jin ji n ji 
CPUプログラム  fの更新  fnからfn+1を計算  fn+1からfn+2を計算  今の時刻から次の時刻を求める  求められた次の時刻を今の時刻と見なし，次の時刻を求める void update(double *f, double *f_new){ int i,j,ij; for(j=0;j<Ny;j++){ for(i=0;i<Nx;i++){ ij = i+Nx*j; f[ij] = f_new[ij]; } } } GPGPU実践プログラミング48 2015/07/01 同じアルゴリズム
#include<stdio.h> #include<stdlib.h> #include<math.h> #define Lx (1.0) #define Ly (1.0) #define Nx 2048 #define Ny Nx #define dx (Lx/(Nx‐1)) #define dy (Ly/(Ny‐1)) #define dt 0.000001 #define endT (1.0) #define Nt (int)(endT/dt) #define DIFF (0.01) #define dxdx (dx*dx) #define dydy (dy*dy) #define Nbytes (Nx*Ny*sizeof(double)) #include "dif1.cu" //#include "dif2.cu" //#include "dif3.cu" int main(void){ int n; double *dev_f,*dev_f_new,*dev_f_lap; dim3 Thread, Block; if(DIFF*dt/dxdx > 0.5){ printf("configuration error¥n"); exit(1); } cudaMalloc( (void**)&dev_f , Nbytes ); cudaMalloc( (void**)&dev_f_new, Nbytes ); cudaMalloc( (void**)&dev_f_lap, Nbytes ); Thread = dim3(THREADX,THREADY,1); Block  = dim3(BLOCKX ,BLOCKY, 1); init<<<Block, Thread>>> (dev_f, dev_f_lap, dev_f_new); for(n=1;n<=Nt;n++){ laplacian<<<Block, Thread>>>(dev_f,dev_f_lap); integrate<<<Block, Thread>>> (dev_f,dev_f_lap,dev_f_new); update<<<Block, Thread>>>(dev_f,dev_f_new); cudaDeviceSynchronize(); } return 0; } GPUプログラム（CPU処理用共通部分） 2015/07/01GPGPU実践プログラミング49 diffusion.cu
#define THREADX 16 #define THREADY 16 #define BLOCKX  (Nx/THREADX) #define BLOCKY  (Ny/THREADY) __global__ void laplacian(double *f, double *f_lap){ int i,j,ij,im1j,ip1j,ijm1,ijp1; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij  =i  +Nx* j; im1j=i‐1+Nx* j;   if(i‐1< 0 )im1j=i+1+Nx*j; ip1j=i+1+Nx* j;   if(i+1>=Nx)ip1j=i‐1+Nx*j; ijm1=i  +Nx*(j‐1);if(j‐1< 0 )ijm1=i  +Nx*(j+1); ijp1=i  +Nx*(j+1);if(j+1>=Ny)ijp1=i  +Nx*(j‐1); f_lap[ij] = (f[ip1j]‐2.0*f[ij]+f[im1j])/dxdx +(f[ijp1]‐2.0*f[ij]+f[ijm1])/dydy; } __global__ void integrate (double *f, double *f_lap, double *f_new){ int i,j,ij; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij =  i+Nx*j; f_new[ij] = f[ij] + dt*DIFF*f_lap[ij]; } __global__ void update(double *f, double *f_new){ int i,j,ij; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij  =  i+Nx*j; f[ij] = f_new[ij]; } __global__ void init (double *f, double *f_lap, double *f_new){ int i,j,ij; double x,y; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij  =  i+Nx*j; f    [ij] = 0.0; f_lap[ij] = 0.0; f_new[ij] = 0.0; x=i*dx‐Lx/2.0; y=j*dy‐Ly/2.0; if(sqrt(x*x+y*y)<=0.2) f[ij] = 1.0; } GPUプログラム（1スレッドが1点を計算） 2015/07/01GPGPU実践プログラミング50 dif1.cu
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング51  2次元，3次元データをプロットするアプリケーション  コマンドラインで命令を実行してグラフを描画  関数の描画，ファイルから読み込んだデータの表示が可能  tesla??では正しく動作しないため，grouseで実行する こと
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング52  表示可能なファイルフォーマット  データはスペース区切り  3次元表示では列（または行）の区切りとして空白行が必要 ‐0.500000 ‐0.500000 0.000000e+00 ‐0.499022 ‐0.500000 0.000000e+00 ... 0.499022 ‐0.500000 0.000000e+00 0.500000 ‐0.500000 0.000000e+00 <‐改行 ‐0.500000 ‐0.499022 0.000000e+00 ‐0.499022 ‐0.499022 0.000000e+00 ... 0.499022 ‐0.499022 0.000000e+00 0.500000 ‐0.499022 0.000000e+00 <‐改行 ‐0.500000 ‐0.498045 0.000000e+00 ‐0.499022 ‐0.498045 0.000000e+00
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング53  スクリプトの実行  gnuplotのコマンドを記述したファイルを実行  load 'スクリプトファイル名'  anim.gpl  結果を単色の等値面で3次元表示  anim_color.gpl  結果をカラーの等値面で3次元表示  anim_2d.gpl  結果をカラーの等高線で2次元表示
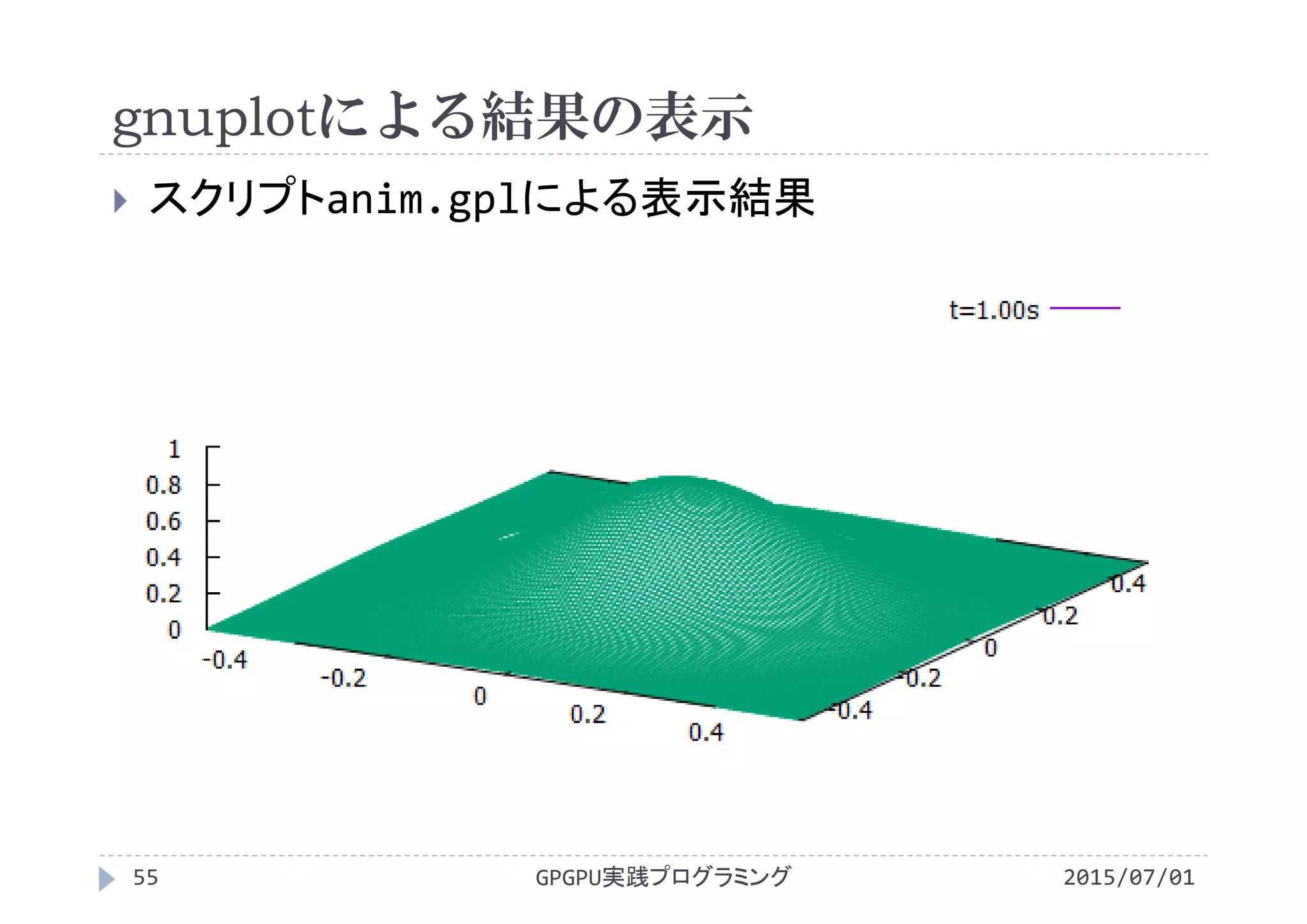
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング54  スクリプトanim.gplの内容 set xrange [‐0.5:0.5] x軸の表示範囲を‐0.5~0.5に固定 set yrange [‐0.5:0.5] y軸の表示範囲を‐0.5~0.5に固定 set zrange [0:1] z軸の表示範囲を0~1に固定 set ticslevel 0 xy平面とz軸の最小値表示位置の差 set hidden3d 隠線消去をする set view 45,30 視点をx方向45°,y方向30°に設定 set size 1,0.75 グラフの縦横比を1:0.75 unset contour 2次元等高線は表示しない set surface 3次元で等値面を表示 unset pm3d カラー表示はしない 以下でファイルを読み込み，3次元表示 splot 'f0.00.txt' using 1:2:3 with line title "t=0.00s"   ... splot 'f1.00.txt' using 1:2:3 with line title "t=1.00s"  
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング55  スクリプトanim.gplによる表示結果
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング56  スクリプトanim_color.gplの内容 set xrange [‐0.5:0.5] x軸の表示範囲を‐0.5~0.5に固定 set yrange [‐0.5:0.5] y軸の表示範囲を‐0.5~0.5に固定 set zrange [0:1] z軸の表示範囲を0~1に固定 set ticslevel 0 xy平面とz軸の最小値表示位置の差 set hidden3d 隠線消去をする set view 45,30 視点をx方向45°,y方向30°に設定 set size 1,0.75 グラフの縦横比を1:0.75 unset contour 2次元等高線は表示しない set surface 3次元で等値面を表示 set pm3d カラー表示する set cbrange[0:1] カラーバーの表示範囲を0~1に固定 以下でファイルを読み込み，3次元表示 splot 'f0.00.txt' using 1:2:3 with line title "t=0.00s"   ... splot 'f1.00.txt' using 1:2:3 with line title "t=1.00s"  
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング57  スクリプトanim_color.gplによる表示結果
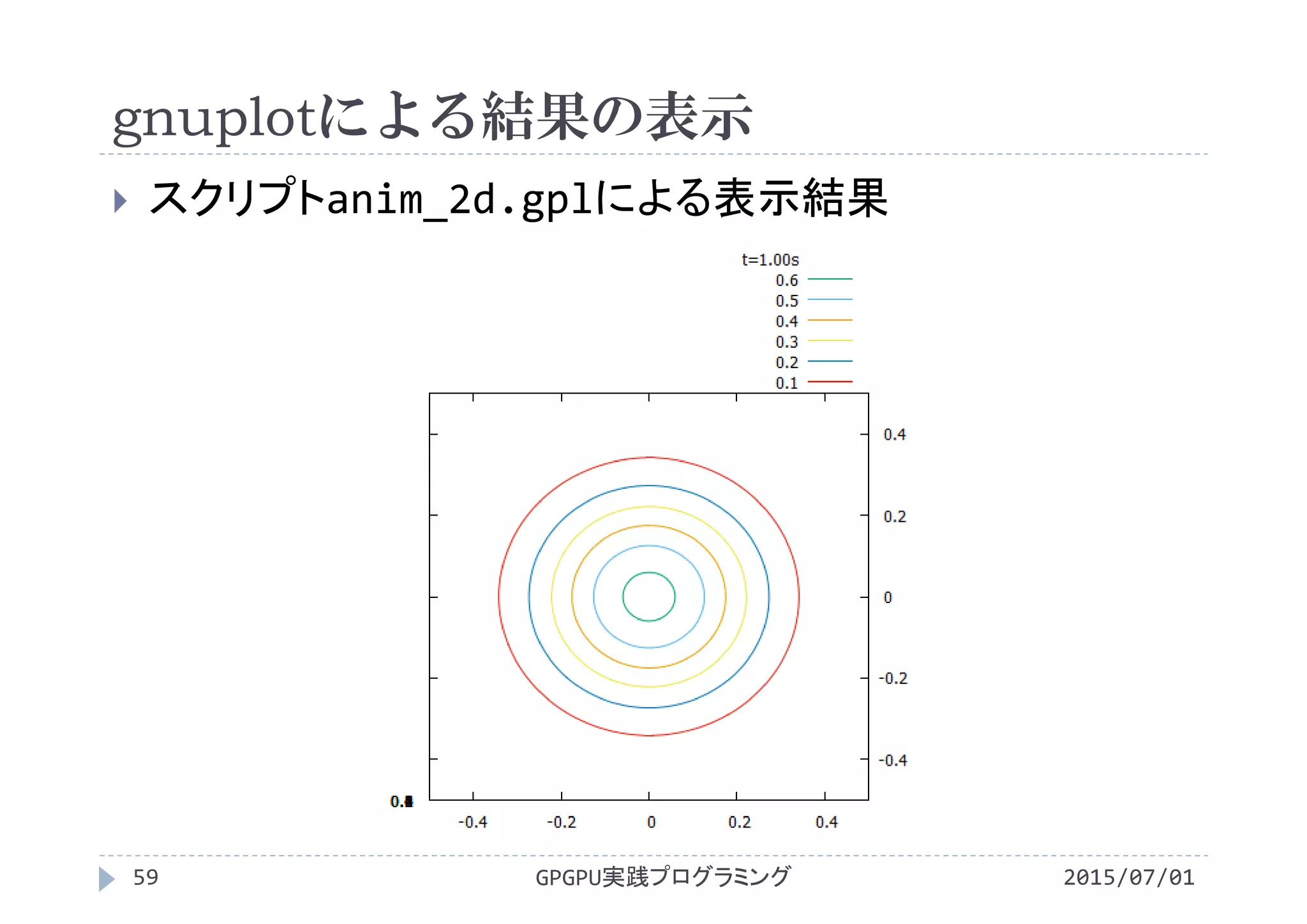
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング58  スクリプトanim_2d.gplの内容 set xrange [‐0.5:0.5] x軸の表示範囲を‐0.5~0.5に固定 set yrange [‐0.5:0.5] y軸の表示範囲を‐0.5~0.5に固定 set zrange [0:1] z軸の表示範囲を0~1に固定 set view 0,0 真上から見下ろす set size 1,1 グラフの縦横比を1:1 set contour 2次元等高線を表示 unset surface 3次元で等値面を表示しない unset pm3d カラー表示しない set cntrparam levels incremental 0,0.1,1 等高線を0から1まで0.1刻みに設定 以下でファイルを読み込み，3次元表示 splot 'f0.00.txt' using 1:2:3 with line title "t=0.00s"   ... splot 'f1.00.txt' using 1:2:3 with line title "t=1.00s"  
gnuplotによる結果の表示 2015/07/01GPGPU実践プログラミング59  スクリプトanim_2d.gplによる表示結果
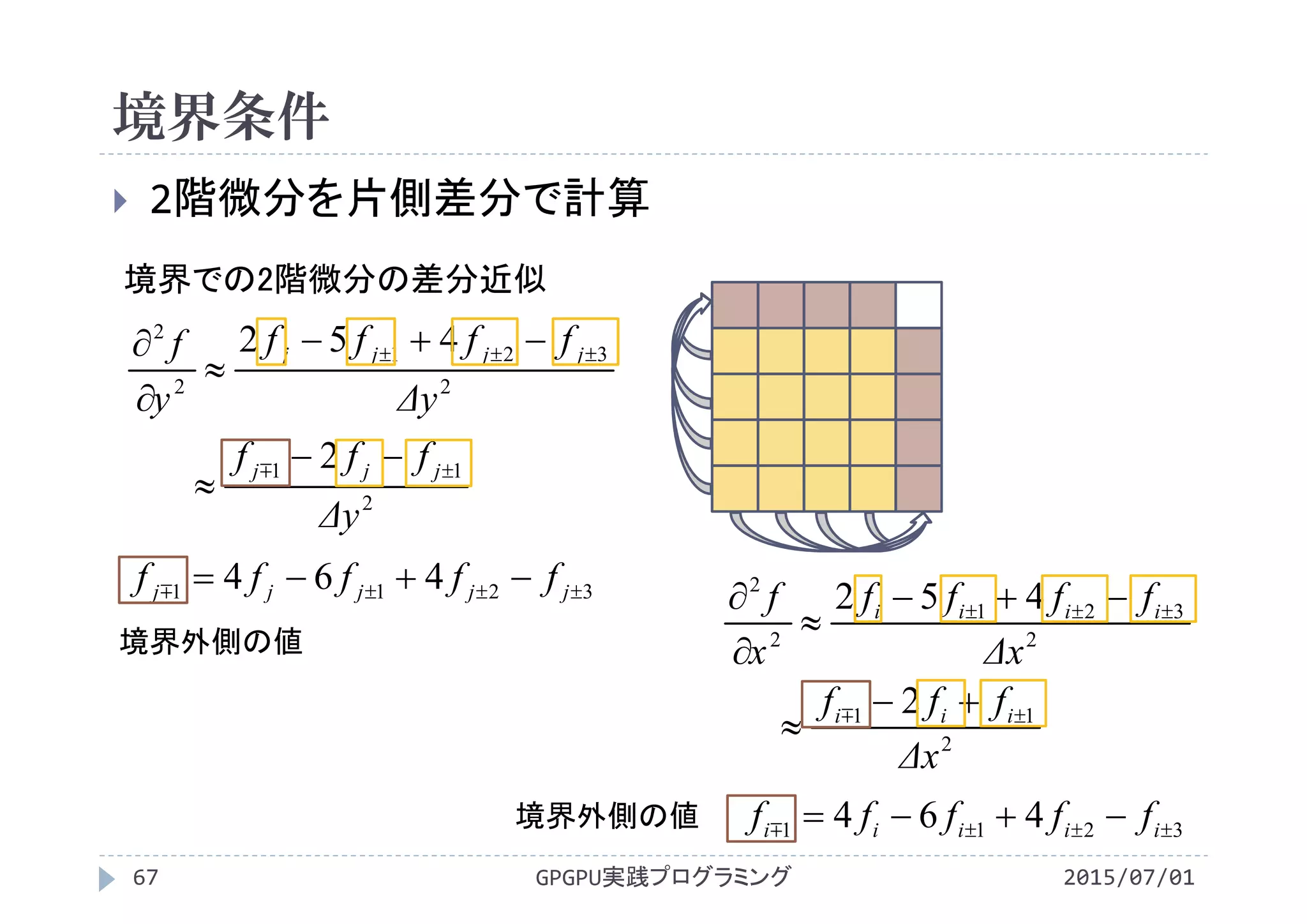
様々な境界条件の計算  共有メモリを利用してキャッシュを模擬  共有メモリに付加的な領域を追加  袖領域 GPGPU実践プログラミング60 2015/07/01 f[] f_lap[]
様々な境界条件の計算  共有メモリを利用してキャッシュを模擬  共有メモリに付加的な領域を追加 GPGPU実践プログラミング61 2015/07/01 f[] f_lap[]
様々な境界条件の計算  共有メモリを利用してキャッシュを模擬  共有メモリに付加的な領域を追加 GPGPU実践プログラミング62 2015/07/01 f[] sf[][] f_lap[]
付加的な領域（袖領域）の取り扱い  データがグローバルメモリに存在する場合は，グローバ ルメモリから読み込み GPGPU実践プログラミング63 2015/07/01 f[] sf[][] f_lap[]
付加的な領域（袖領域）の取り扱い  グローバルメモリに無い場合は境界条件から決定 GPGPU実践プログラミング64 2015/07/01 f[] sf[][] f_lap[]
境界条件 2015/07/01GPGPU実践プログラミング65  1階微分が0 0 2 1,1,       Δy ff y f jiji 1,1, jiji ff  0 2 ,1,1       Δx ff x u jiji jiji ff ,1,1 
境界条件 2015/07/01GPGPU実践プログラミング66  2階微分が0 0 2 2 ,1,,1 2 2       Δx fff x f jijiji jijiji fff ,1,,1 2  1,,1, 2 jijiji fff  0 2 2 1,,1, 2 2       Δy fff y f jijiji
境界条件 2015/07/01GPGPU実践プログラミング67  2階微分を片側差分で計算 3211 464   jjjjj fffff  2 11 2 321 2 2 2 452 Δy fff Δy ffff y f jjj jjjj          2 11 2 321 2 2 2 452 Δx fff Δx ffff x f iii iiii          3211 464   iiiii fffff  境界での2階微分の差分近似 境界外側の値 境界外側の値
#define THREADX 16 #define THREADY 16 #define BLOCKX  (Nx/THREADX) #define BLOCKY  (Ny/THREADY) __global__ void laplacian(double *f, double *f_lap){ int i,j,ij; int tx,ty; __shared__ float sf[1+THREADX+1][1+THREADY+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x + 1; ty = threadIdx.y + 1; ij = i+Nx*j; sf[tx][ty] = f[ij]; __syncthreads(); if(blockIdx.x == 0 && threadIdx.x == 0) sf[tx‐1][ty] = sf[tx+1][ty]; if(blockIdx.x != 0 && threadIdx.x == 0) sf[tx‐1][ty] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1  && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] = sf[tx‐1][ty]; if(blockIdx.x != gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] =  f[i+1+Nx*j]; if(blockIdx.y == 0 && threadIdx.y == 0) sf[tx][ty‐1] = sf[tx][ty+1]; if(blockIdx.y != 0 && threadIdx.y == 0) sf[tx][ty‐1] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] = sf[tx][ty‐1]; if(blockIdx.y != gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] =  f[i+Nx*(j+1)]; __syncthreads(); f_lap[ij] = (sf[tx‐1][ty  ]‐2.0*sf[tx][ty]+sf[tx+1][ty  ])/dxdx +(sf[tx  ][ty‐1]‐2.0*sf[tx][ty]+sf[tx  ][ty+1])/dydy; } GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング68 dif2.cu
GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング69  ブロック内のスレッド数＋袖領域分の共有メモ リを確保  袖領域があるために添字の対応が変化  添字の対応を考えないと，必要なデータを袖領域に置い てしまう  __syncthreads()を呼んでスレッドを同期  共有メモリにデータが正しく書き込まれた事を保証 __shared__ float sf[1+THREADX+1][1+THREADY+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x; ty = threadIdx.y;   ij = i+Ny*j; sf[tx][ty] = f[ij]; __syncthreads(); f[] sf[][]
GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング70  ブロック内のスレッド数＋袖領域分の共有メモ リを確保  袖領域があるために添字の対応が変化  添字の対応を考えないと，必要なデータを袖領域に置い てしまう  __syncthreads()を呼んでスレッドを同期  共有メモリにデータが正しく書き込まれた事を保証 __shared__ float sf[1+THREADX+1][1+THREADY+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x + 1; ty = threadIdx.y;   ij = i+Ny*j; sf[tx][ty] = f[ij]; __syncthreads(); f[] sf[][] +1
GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング71  ブロック内のスレッド数＋袖領域分の共有メモ リを確保  袖領域があるために添字の対応が変化  添字の対応を考えないと，必要なデータを袖領域に置い てしまう  __syncthreads()を呼んでスレッドを同期  共有メモリにデータが正しく書き込まれた事を保証 __shared__ float sf[1+THREADX+1][1+THREADY+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x + 1; ty = threadIdx.y + 1;   ij = i+Ny*j; sf[tx][ty] = f[ij]; __syncthreads(); f[] sf[][] +1 +1
GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング72  袖領域の設定 if(blockIdx.x == 0           && threadIdx.x == 0           ) sf[tx‐1][ty] = sf[tx+1][ty]; if(blockIdx.x != 0           && threadIdx.x == 0           ) sf[tx‐1][ty] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] = sf[tx‐1][ty]; if(blockIdx.x != gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] =  f[i+1+Nx*j]; if(blockIdx.y == 0           && threadIdx.y == 0           ) sf[tx][ty‐1] = sf[tx][ty+1]; if(blockIdx.y != 0           && threadIdx.y == 0           ) sf[tx][ty‐1] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] = sf[tx][ty‐1]; if(blockIdx.y != gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] =  f[i+Nx*(j+1)]; __syncthreads();  グローバルメモリにデータがある箇所はグロー バルメモリから読み込み  グローバルメモリにデータがない箇所は2階微 分が0になるように袖領域の値を決定  ブロックが境界に接しているか否かで処理を切替
GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング73  共有メモリのデータを利用してラプラシアンを計算  if分岐を排除 f_lap[ij] = (sf[tx‐1][ty  ]‐2.0*sf[tx][ty]+sf[tx+1][ty  ])/dxdx +(sf[tx  ][ty‐1]‐2.0*sf[tx][ty]+sf[tx  ][ty+1])/dydy; f_lap[] sf[][]
2次元的な配列アクセスの優先方向 2015/07/01GPGPU実践プログラミング74  CUDAで2次元的に並列化してアクセ スする場合  threadIdx.xのスレッド群（threadId x.yが一定）が連続なメモリアドレスに アクセス  C言語の多次元配列  2次元目の要素が連続になるようメモリ に確保  dif2.cuの共有メモリの使い方は不 適切 sf[THREADX+2][THREADY+2] threadIdx.x threadIdx.y THREADX+2 THREADY+2 f[] Nx Ny j i threadIdx.x threadIdx.y
2次元的な配列アクセスの優先方向 2015/07/01GPGPU実践プログラミング75  共有メモリの宣言の変更  1次元目と2次元目を入れ替え  sf[1+THREADX+1][1+THREADY+1]  sf[1+THREADY+1][1+THREADX+1]  配列参照  1次元目の添字はthreadIdx.yを利用  2次元目の添字はthreadIdx.xを利用  threadIdx.xのスレッド群（threadIdx.y が一定）が連続なメモリアドレスにアクセス sf[THREADX+2][THREADY+2] threadIdx.x threadIdx.y THREADX+2 THREADY+2 sf[THREADY+2][THREADX+2] threadIdx.y threadIdx.x THREADY+2 THREADX+2
#define THREADX 16 #define THREADY 16 #define BLOCKX  (Nx/THREADX) #define BLOCKY  (Ny/THREADY) __global__ void laplacian(double *f, double *f_lap){ int i,j,ij; int tx,ty; __shared__ float sf[1+THREADX+1][1+THREADY+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x + 1; ty = threadIdx.y + 1; ij = i+Nx*j; sf[tx][ty] = f[ij]; __syncthreads(); if(blockIdx.x == 0 && threadIdx.x == 0) sf[tx‐1][ty] = sf[tx+1][ty]; if(blockIdx.x != 0 && threadIdx.x == 0) sf[tx‐1][ty] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1  && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] = sf[tx‐1][ty]; if(blockIdx.x != gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[tx+1][ty] =  f[i+1+Nx*j]; if(blockIdx.y == 0 && threadIdx.y == 0) sf[tx][ty‐1] = sf[tx][ty+1]; if(blockIdx.y != 0 && threadIdx.y == 0) sf[tx][ty‐1] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] = sf[tx][ty‐1]; if(blockIdx.y != gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[tx][ty+1] =  f[i+Nx*(j+1)]; __syncthreads(); f_lap[ij] = (sf[tx‐1][ty  ]‐2.0*sf[tx][ty]+sf[tx+1][ty  ])/dxdx +(sf[tx  ][ty‐1]‐2.0*sf[tx][ty]+sf[tx  ][ty+1])/dydy; } GPUプログラム（ラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング76 dif2.cu
#define THREADX 16 #define THREADY 16 #define BLOCKX  (Nx/THREADX) #define BLOCKY  (Ny/THREADY) __global__ void laplacian(double *f, double *f_lap){ int i,j,ij; int tx,ty; __shared__ float sf[1+THREADY+1][1+THREADX+1]; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; tx = threadIdx.x + 1; ty = threadIdx.y + 1; ij = i+Nx*j; sf[ty][tx] = f[ij]; __syncthreads(); if(blockIdx.x == 0 && threadIdx.x == 0) sf[ty][tx‐1] = sf[ty][tx+1]; if(blockIdx.x != 0 && threadIdx.x == 0) sf[ty][tx‐1] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1  && threadIdx.x == blockDim.x‐1) sf[ty][tx+1] = sf[ty][tx‐1]; if(blockIdx.x != gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[ty][tx+1] =  f[i+1+Nx*j]; if(blockIdx.y == 0 && threadIdx.y == 0) sf[ty‐1][tx] = sf[ty+1][tx]; if(blockIdx.y != 0 && threadIdx.y == 0) sf[ty‐1][tx] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[ty+1][tx] = sf[ty‐1][tx]; if(blockIdx.y != gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[ty+1][tx] =  f[i+Nx*(j+1)]; __syncthreads(); f_lap[ij] = (sf[ty  ][tx‐1]‐2.0*sf[ty][tx]+sf[ty  ][tx+1])/dxdx +(sf[ty‐1][tx  ]‐2.0*sf[ty][tx]+sf[ty+1][tx  ])/dydy; } GPUプログラム（共有メモリの添字を交換 したラプラシアンカーネル） 2015/07/01GPGPU実践プログラミング77 dif3.cu
ラプラシアンカーネルの実行時間の比較 2015/07/01GPGPU実践プログラミング78  格子分割数 Nx×Ny=2048×2048  1ブロックあたりのスレッド数 16×16  その他カーネルの実行時間  integrate 900s  update 600s ラブラシアンカーネル 実行時間 [s] dif1版 1998 dif2版 2286 1900（袖領域の設定を除く） dif3版 2302 1900（袖領域の設定を除く）
GPUプログラムの評価 2015/07/01GPGPU実践プログラミング79  共有メモリを使用したdif3.cu  dif1.cu（共有メモリ不使用）と比較して遅い  Fermi世代以降のGPUはキャッシュを搭載  共有メモリを使っても速くならない  共有メモリへ明示的にデータを移動  余分な処理により負荷が増加  せっかくなのでif文の書き方について評価
GPUプログラムの評価 2015/07/01GPGPU実践プログラミング80  if分岐の書き方による実行速度の変化  ブロックとスレッドの条件を同時に記述  Warp内のスレッドが分岐すると実行速度が著しく低下  GPUはブロック単位で分岐，Warp単位で分岐しても実行速度 の低下は抑えられる  上の書き方は最適ではない？  ブロック単位の分岐とスレッド単位の分岐を同時に記述 if(blockIdx.x == 0           && threadIdx.x == 0           ) sf[ty][tx‐1] = sf[ty][tx+1]; if(blockIdx.x != 0           && threadIdx.x == 0           ) sf[ty][tx‐1] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[ty][tx+1] = sf[ty][tx‐1]; if(blockIdx.x != gridDim.x‐1 && threadIdx.x == blockDim.x‐1) sf[ty][tx+1] =  f[i+1+Nx*j]; if(blockIdx.y == 0           && threadIdx.y == 0           ) sf[ty‐1][tx] = sf[ty+1][tx]; if(blockIdx.y != 0           && threadIdx.y == 0           ) sf[ty‐1][tx] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[ty+1][tx] = sf[ty‐1][tx]; if(blockIdx.y != gridDim.y‐1 && threadIdx.y == blockDim.y‐1) sf[ty+1][tx] =  f[i+Nx*(j+1)];
GPUプログラムの評価 2015/07/01GPGPU実践プログラミング81  if分岐の書き方による実行速度の変化  ブロックとスレッドの条件を分け，ifを入れ子に  ブロック単位で分岐した後，スレッド単位で分岐  ブロック単位での分岐による速度低下が抑えられそうな気がする  ブロック単位の分岐を記述する8個のifは2個一組（同じ色の 行）で排他的に分岐  blockIdx.x==0が成立すると，blockIdx!=0は絶対に成立しない if(blockIdx.x == 0          )if(threadIdx.x == 0           ) sf[ty][tx‐1] = sf[ty][tx+1]; if(blockIdx.x != 0          )if(threadIdx.x == 0           ) sf[ty][tx‐1] =  f[i‐1+Nx*j]; if(blockIdx.x == gridDim.x‐1)if(threadIdx.x == blockDim.x‐1) sf[ty][tx+1] = sf[ty][tx‐1]; if(blockIdx.x != gridDim.x‐1)if(threadIdx.x == blockDim.x‐1) sf[ty][tx+1] =  f[i+1+Nx*j]; if(blockIdx.y == 0          )if(threadIdx.y == 0           ) sf[ty‐1][tx] = sf[ty+1][tx]; if(blockIdx.y != 0          )if(threadIdx.y == 0           ) sf[ty‐1][tx] =  f[i+Nx*(j‐1)]; if(blockIdx.y == gridDim.y‐1)if(threadIdx.y == blockDim.y‐1) sf[ty+1][tx] = sf[ty‐1][tx]; if(blockIdx.y != gridDim.y‐1)if(threadIdx.y == blockDim.y‐1) sf[ty+1][tx] =  f[i+Nx*(j+1)];
GPUプログラムの評価 2015/07/01GPGPU実践プログラミング82  if分岐の書き方による実行速度の変化  2個一組のifの片方をelseに書き換え  2個一組のifにおける条件判断は1回限り  2回ifの条件判断を行うよりは速いような気がする if(blockIdx.x == 0          ){if(threadIdx.x == 0           ) sf[ty][tx‐1] = sf[ty][tx+1];} else                         {if(threadIdx.x == 0           ) sf[ty][tx‐1] =  f[i‐1+Nx*j];} if(blockIdx.x == gridDim.x‐1){if(threadIdx.x == blockDim.x‐1) sf[ty][tx+1] = sf[ty][tx‐1];} else                         {if(threadIdx.x == blockDim.x‐1) sf[ty][tx+1] =  f[i+1+Nx*j];} if(blockIdx.y == 0          ){if(threadIdx.y == 0           ) sf[ty‐1][tx] = sf[ty+1][tx];} else                         {if(threadIdx.y == 0           ) sf[ty‐1][tx] =  f[i+Nx*(j‐1)];} if(blockIdx.y == gridDim.y‐1){if(threadIdx.y == blockDim.y‐1) sf[ty+1][tx] = sf[ty‐1][tx];} else                         {if(threadIdx.y == blockDim.y‐1) sf[ty+1][tx] =  f[i+Nx*(j+1)];}
if分岐の書き方の違いによる実行速度の変化 2015/07/01GPGPU実践プログラミング83  格子分割数 Nx×Ny=2048×2048  1ブロックあたりのスレッド数 16×16 if文の書き方 実行時間 [ms] ブロックとスレッドの条件 を同時に記述 2.30 ブロックとスレッドの条件 を分け，ifを入れ子に 2.51 2個一組のifの片方を elseに書き換え 2.35 カーネル1 （共有メモリ不使用） 2.00
その他の処理の高速化 2015/07/01GPGPU実践プログラミング84  laplacianカーネルとintegrateカーネルの融合  カーネルフュージョン(kernel fusion)  異なる処理を行うカーネルをまとめることでデータを再利用  グローバルメモリへの書き込み，読み出しを回避 __global__ void integrate(double *f, double *f_new){ int i,j,ij; double f_lap; //ある1点のラプラシアンを計算してレジスタに保存 i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij= i+Nx*j; f_lap = ... f_new[ij] = f[ij] + dt*DIFF*f_lap; //f[ij]=f[ij]+...とすると，全ての点のf_lapを計算する前にfを更新する可能性がある }
その他の処理の高速化 2015/07/01GPGPU実践プログラミング85  値の更新  f_newのデータをfにコピーしているだけ  cudaMemcpyで代用可能 __global__ void update(double *f, double *f_new){ int i,j,ij; i = blockIdx.x*blockDim.x + threadIdx.x; j = blockIdx.y*blockDim.y + threadIdx.y; ij =  i+Nx*j; f[ij] = f_new[ij]; }
その他の処理の高速化 2015/07/01GPGPU実践プログラミング86  値の更新  f_newのデータをfにコピーしているだけ  cudaMemcpyで代用可能 for(n=1;n<=Nt;n++){ integrate<<<Block, Thread>>>(dev_f,dev_f_new); //update<<<Block, Thread>>>(dev_f,dev_f_new); cudaMemcpy(dev_f, dev_f_new, Nbytes, cudaMemcpyDeviceToDevice); } return 0;
その他の処理の高速化 2015/07/01GPGPU実践プログラミング87  値の更新  ダブルバッファリング（第7回授業参照）でコピーを回避するこ とも可能 double *dev_f[2]; int in=0;out=1‐in; cudaMalloc((void **)&dev_f[in ],Nbytes); cudaMalloc((void **)&dev_f[out],Nbytes); init<<<Block, Thread>>>(dev_f[in(=0)], dev_f[out(=1)]); for(n=1;n<=Nt;n++){//n=1 integrate<<<Block, Thread>>>(dev_f[in(=0)],dev_f[out(=1)]); in = out; out = 1‐in; //in=1, out=0 }
その他の処理の高速化 2015/07/01GPGPU実践プログラミング88  値の更新  ダブルバッファリング（第7回授業参照）でコピーを回避するこ とも可能 double *dev_f[2]; int in=0;out=1‐in; cudaMalloc((void **)&dev_f[in ],Nbytes); cudaMalloc((void **)&dev_f[out],Nbytes); init<<<Block, Thread>>>(dev_f[in(=0)], dev_f[out(=1)]); for(n=1;n<=Nt;n++){//n=2 integrate<<<Block, Thread>>>(dev_f[in(=1)],dev_f[out(=0)]); in = out; out = 1‐in; //in=0, out=1 }
その他の処理の高速化 2015/07/01GPGPU実践プログラミング89  値の更新  ダブルバッファリング（第7回授業参照）でコピーを回避するこ とも可能 dev_f[0] 時刻n dev_f[1] 時刻n+1 integrate<<<Block, Thread>>>(dev_f[in(=0)],dev_f[out(=1)]);
その他の処理の高速化 2015/07/01GPGPU実践プログラミング90  値の更新  ダブルバッファリング（第7回授業参照）でコピーを回避するこ とも可能 dev_f[0] 時刻n+1 dev_f[1] 時刻n integrate<<<Block, Thread>>>(dev_f[in(=1)],dev_f[out(=0)]);

More Related Content

PDF
プログラムを高速化する話Ⅱ 〜GPGPU編〜
by京大 マイコンクラブ
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第9回　偏微分方程式の差分計算 （移流方程式）
by智啓 出川
 
PDF
「NVIDIA プロファイラを用いたPyTorch学習最適化手法のご紹介(修正版)」
byManaMurakami1
 
PDF
2015年度GPGPU実践基礎工学　第10回　GPUのプログラム構造
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第2回　GPUによる並列計算の概念と メモリアクセス
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第10回　Poisson方程式の求解 （線形連立一次方程式）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第11回　数値流体力学への応用 （支配方程式，CPUプログラム）
by智啓 出川
 
PDF
CUDAプログラミング入門
byNVIDIA Japan
 
プログラムを高速化する話Ⅱ 〜GPGPU編〜
by京大 マイコンクラブ
 
2015年度先端GPGPUシミュレーション工学特論　第9回　偏微分方程式の差分計算 （移流方程式）
by智啓 出川
 
「NVIDIA プロファイラを用いたPyTorch学習最適化手法のご紹介(修正版)」
byManaMurakami1
 
2015年度GPGPU実践基礎工学　第10回　GPUのプログラム構造
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第2回　GPUによる並列計算の概念と メモリアクセス
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第10回　Poisson方程式の求解 （線形連立一次方程式）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第11回　数値流体力学への応用 （支配方程式，CPUプログラム）
by智啓 出川
 
CUDAプログラミング入門
byNVIDIA Japan
 

What's hot

PDF
2015年度先端GPGPUシミュレーション工学特論　第8回　偏微分方程式の差分計算 （拡散方程式）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第7回　総和計算
by智啓 出川
 
PDF
GPGPU Seminar (GPU Accelerated Libraries, 3 of 3, Thrust)
by智啓 出川
 
PDF
マルチコアを用いた画像処理
byNorishige Fukushima
 
PDF
GPGPU Seminar (GPU Accelerated Libraries, 1 of 3, cuBLAS)
by智啓 出川
 
PDF
RAPIDS 概要
byNVIDIA Japan
 
PDF
CPU / GPU高速化セミナー！性能モデルの理論と実践：実践編
byFixstars Corporation
 
PDF
いまさら聞けない！CUDA高速化入門
byFixstars Corporation
 
PDF
GPU と PYTHON と、それから最近の NVIDIA
byNVIDIA Japan
 
PDF
組み込み関数（intrinsic）によるSIMD入門
byNorishige Fukushima
 
PDF
PCAの最終形態GPLVMの解説
by弘毅 露崎
 
PDF
ゲーム開発者のための C++11/C++14
byRyo Suzuki
 
PDF
CUDAのアセンブリ言語基礎のまとめ　PTXとSASSの概説
byTakateru Yamagishi
 
PDF
2015年度GPGPU実践プログラミング　第15回　GPU最適化ライブラリ
by智啓 出川
 
PDF
ガイデットフィルタとその周辺
byNorishige Fukushima
 
PDF
深層生成モデルと世界モデル
byMasahiro Suzuki
 
PDF
ARM CPUにおけるSIMDを用いた高速計算入門
byFixstars Corporation
 
PDF
NVIDIA HPC ソフトウエア斜め読み
byNVIDIA Japan
 
PPTX
猫でも分かるVariational AutoEncoder
bySho Tatsuno
 
PDF
2015年度GPGPU実践プログラミング　第9回　行列計算（行列－行列積）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第8回　偏微分方程式の差分計算 （拡散方程式）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第7回　総和計算
by智啓 出川
 
GPGPU Seminar (GPU Accelerated Libraries, 3 of 3, Thrust)
by智啓 出川
 
マルチコアを用いた画像処理
byNorishige Fukushima
 
GPGPU Seminar (GPU Accelerated Libraries, 1 of 3, cuBLAS)
by智啓 出川
 
RAPIDS 概要
byNVIDIA Japan
 
CPU / GPU高速化セミナー！性能モデルの理論と実践：実践編
byFixstars Corporation
 
いまさら聞けない！CUDA高速化入門
byFixstars Corporation
 
GPU と PYTHON と、それから最近の NVIDIA
byNVIDIA Japan
 
組み込み関数（intrinsic）によるSIMD入門
byNorishige Fukushima
 
PCAの最終形態GPLVMの解説
by弘毅 露崎
 
ゲーム開発者のための C++11/C++14
byRyo Suzuki
 
CUDAのアセンブリ言語基礎のまとめ　PTXとSASSの概説
byTakateru Yamagishi
 
2015年度GPGPU実践プログラミング　第15回　GPU最適化ライブラリ
by智啓 出川
 
ガイデットフィルタとその周辺
byNorishige Fukushima
 
深層生成モデルと世界モデル
byMasahiro Suzuki
 
ARM CPUにおけるSIMDを用いた高速計算入門
byFixstars Corporation
 
NVIDIA HPC ソフトウエア斜め読み
byNVIDIA Japan
 
猫でも分かるVariational AutoEncoder
bySho Tatsuno
 
2015年度GPGPU実践プログラミング　第9回　行列計算（行列－行列積）
by智啓 出川
 

Viewers also liked

PDF
2015年度GPGPU実践プログラミング　第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第8回　総和計算（高度な最適化）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第5回　GPUのメモリ階層
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第10回　行列計算（行列－行列積の高度な最適化）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第1回　GPGPUの歴史と応用例
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第12回　GPUによる画像処理
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第13回　GPUのメモリ階層
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第6回　パフォーマンス解析ツール
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第2回　GPUのアーキテクチャとプログラム構造
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第14回　N体問題
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第6回　ソフトウェアによるCPUの高速化技術
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第7回　シングルコアとマルチコア
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第3回　GPUクラスタ上でのプログラミング（CUDA）
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第4回　CPUのアーキテクチャ
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第13回　多粒子の運動
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第5回　ハードウェアによるCPUの高速化技術
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第1回　学際的分野における先端シミュレーション技術の歴史
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第11回　画像処理
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第8回　並列計算の概念 （プロセスとスレッド）
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第9回補足　GROUSEの利用方法
by智啓 出川
 
2015年度GPGPU実践プログラミング　第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第8回　総和計算（高度な最適化）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第5回　GPUのメモリ階層
by智啓 出川
 
2015年度GPGPU実践プログラミング　第10回　行列計算（行列－行列積の高度な最適化）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第1回　GPGPUの歴史と応用例
by智啓 出川
 
2015年度GPGPU実践基礎工学　第12回　GPUによる画像処理
by智啓 出川
 
2015年度GPGPU実践基礎工学　第13回　GPUのメモリ階層
by智啓 出川
 
2015年度GPGPU実践プログラミング　第6回　パフォーマンス解析ツール
by智啓 出川
 
2015年度GPGPU実践プログラミング　第2回　GPUのアーキテクチャとプログラム構造
by智啓 出川
 
2015年度GPGPU実践プログラミング　第14回　N体問題
by智啓 出川
 
2015年度GPGPU実践基礎工学　第6回　ソフトウェアによるCPUの高速化技術
by智啓 出川
 
2015年度GPGPU実践基礎工学　第7回　シングルコアとマルチコア
by智啓 出川
 
2015年度GPGPU実践基礎工学　第3回　GPUクラスタ上でのプログラミング（CUDA）
by智啓 出川
 
2015年度GPGPU実践基礎工学　第4回　CPUのアーキテクチャ
by智啓 出川
 
2015年度GPGPU実践プログラミング　第13回　多粒子の運動
by智啓 出川
 
2015年度GPGPU実践基礎工学　第5回　ハードウェアによるCPUの高速化技術
by智啓 出川
 
2015年度GPGPU実践基礎工学　第1回　学際的分野における先端シミュレーション技術の歴史
by智啓 出川
 
2015年度GPGPU実践プログラミング　第11回　画像処理
by智啓 出川
 
2015年度GPGPU実践基礎工学　第8回　並列計算の概念 （プロセスとスレッド）
by智啓 出川
 
2015年度GPGPU実践基礎工学　第9回補足　GROUSEの利用方法
by智啓 出川
 

Similar to 2015年度GPGPU実践プログラミング　第12回　偏微分方程式の差分計算

PDF
GPGPU Seminar (GPU Accelerated Libraries, 2 of 3, cuSPARSE)
by智啓 出川
 
PDF
GPGPU Seminar (PyCUDA)
by智啓 出川
 
PDF
動的計画法の並列化
byProktmr
 
PDF
アプリケーションの性能最適化１（高並列性能最適化）
byRCCSRENKEI
 
PDF
高速な倍精度指数関数expの実装
byMITSUNARI Shigeo
 
PDF
1072: アプリケーション開発を加速するCUDAライブラリ
byNVIDIA Japan
 
PDF
第6回 配信講義 計算科学技術特論A（2021）
byRCCSRENKEI
 
PDF
optimal Ate pairing
byMITSUNARI Shigeo
 
PPTX
8 並列計算に向けた pcセッティング
byTakeshi Takaishi
 
PDF
200702material hirokawa
byRCCSRENKEI
 
PDF
200625material naruse
byRCCSRENKEI
 
KEY
PyOpenCLによるGPGPU入門 Tokyo.SciPy#4 編
byYosuke Onoue
 
KEY
NVIDIA Japan Seminar 2012
byTakuro Iizuka
 
PPTX
GPUによる多倍長整数乗算の高速化手法の提案
byKoji Kitano
 
PDF
2015年度GPGPU実践基礎工学　第11回　GPUでの並列 プログラミング（ベクトル和）
by智啓 出川
 
PDF
GPGPU Education at Nagaoka University of Technology: A Trial Run
by智啓 出川
 
PDF
CMSI計算科学技術特論B(14) OpenACC・CUDAによるGPUコンピューティング
byComputational Materials Science Initiative
 
PDF
Anaconda & NumbaPro 使ってみた
byYosuke Onoue
 
PDF
2015年度GPGPU実践プログラミング　第3回　GPGPUプログラミング環境
by智啓 出川
 
PDF
20130126 sc12-reading
byToshiya Komoda
 
GPGPU Seminar (GPU Accelerated Libraries, 2 of 3, cuSPARSE)
by智啓 出川
 
GPGPU Seminar (PyCUDA)
by智啓 出川
 
動的計画法の並列化
byProktmr
 
アプリケーションの性能最適化１（高並列性能最適化）
byRCCSRENKEI
 
高速な倍精度指数関数expの実装
byMITSUNARI Shigeo
 
1072: アプリケーション開発を加速するCUDAライブラリ
byNVIDIA Japan
 
第6回 配信講義 計算科学技術特論A（2021）
byRCCSRENKEI
 
optimal Ate pairing
byMITSUNARI Shigeo
 
8 並列計算に向けた pcセッティング
byTakeshi Takaishi
 
200702material hirokawa
byRCCSRENKEI
 
200625material naruse
byRCCSRENKEI
 
PyOpenCLによるGPGPU入門 Tokyo.SciPy#4 編
byYosuke Onoue
 
NVIDIA Japan Seminar 2012
byTakuro Iizuka
 
GPUによる多倍長整数乗算の高速化手法の提案
byKoji Kitano
 
2015年度GPGPU実践基礎工学　第11回　GPUでの並列 プログラミング（ベクトル和）
by智啓 出川
 
GPGPU Education at Nagaoka University of Technology: A Trial Run
by智啓 出川
 
CMSI計算科学技術特論B(14) OpenACC・CUDAによるGPUコンピューティング
byComputational Materials Science Initiative
 
Anaconda & NumbaPro 使ってみた
byYosuke Onoue
 
2015年度GPGPU実践プログラミング　第3回　GPGPUプログラミング環境
by智啓 出川
 
20130126 sc12-reading
byToshiya Komoda
 

More from 智啓 出川

PDF
2015年度先端GPGPUシミュレーション工学特論　第7回　総和計算（Atomic演算）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第4回　GPUのメモリ階層の詳細 （共有メモリ）
by智啓 出川
 
PDF
GPGPU Seminar (GPGPU and CUDA Fortran)
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第6回　プログラムの性能評価指針 (Flop/Byte，計算律速，メモリ律速)
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第5回　GPUのメモリ階層の詳細 （様々なメモリの利用）
by智啓 出川
 
PDF
Fortranが拓く世界、VSCodeが架ける橋
by智啓 出川
 
PDF
Very helpful python code to find coefficients of the finite difference method
by智啓 出川
 
PDF
PGI CUDA FortranとGPU最適化ライブラリの一連携法
by智啓 出川
 
PDF
Pythonによる累乗近似
by智啓 出川
 
PDF
Cuda fortranの利便性を高めるfortran言語の機能
by智啓 出川
 
PDF
オブジェクト指向Fortranが拓く（はずだった）新しい世界
by智啓 出川
 
PDF
数値計算結果のPythonによる後処理について（1次元データのピーク値およびその位置の推定）
by智啓 出川
 
PPTX
Schematic diagrams of GPUs' architecture and Time evolution of theoretical FL...
by智啓 出川
 
PDF
GPGPU Seminar (Accelerataion of Lattice Boltzmann Method using CUDA Fortran)
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第13回　数値流体力学への応用 （高度な最適化）
by智啓 出川
 
PDF
Why do we confuse String and Array of Characters in Fortran?
by智啓 出川
 
PPTX
教育機関でのJetsonの活用の可能性
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第3回　GPUプログラム構造の詳細 （threadとwarp）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第14回　複数GPUの利用
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第15回　CPUとGPUの協調
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第7回　総和計算（Atomic演算）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第4回　GPUのメモリ階層の詳細 （共有メモリ）
by智啓 出川
 
GPGPU Seminar (GPGPU and CUDA Fortran)
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第6回　プログラムの性能評価指針 (Flop/Byte，計算律速，メモリ律速)
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第5回　GPUのメモリ階層の詳細 （様々なメモリの利用）
by智啓 出川
 
Fortranが拓く世界、VSCodeが架ける橋
by智啓 出川
 
Very helpful python code to find coefficients of the finite difference method
by智啓 出川
 
PGI CUDA FortranとGPU最適化ライブラリの一連携法
by智啓 出川
 
Pythonによる累乗近似
by智啓 出川
 
Cuda fortranの利便性を高めるfortran言語の機能
by智啓 出川
 
オブジェクト指向Fortranが拓く（はずだった）新しい世界
by智啓 出川
 
数値計算結果のPythonによる後処理について（1次元データのピーク値およびその位置の推定）
by智啓 出川
 
Schematic diagrams of GPUs' architecture and Time evolution of theoretical FL...
by智啓 出川
 
GPGPU Seminar (Accelerataion of Lattice Boltzmann Method using CUDA Fortran)
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第13回　数値流体力学への応用 （高度な最適化）
by智啓 出川
 
Why do we confuse String and Array of Characters in Fortran?
by智啓 出川
 
教育機関でのJetsonの活用の可能性
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第3回　GPUプログラム構造の詳細 （threadとwarp）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第14回　複数GPUの利用
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第15回　CPUとGPUの協調
by智啓 出川
 

2015年度GPGPU実践プログラミング　第12回　偏微分方程式の差分計算