智出
Uploaded by智啓 出川
PDF, PPTX1,147 views

2015年度GPGPU実践プログラミング　第8回　総和計算（高度な最適化）

長岡技術科学大学 2015年度GPGPU実践プログラミング（全15回，学部4年対象講義） 第8回総和計算（高度な最適化） 2015年度GPGPU実践プログラミング ・第1回　GPGPUの歴史と応用例 http://www.slideshare.net/ssuserf87701/2015gpgpu1-59179080 ・第2回　GPUのアーキテクチャとプログラム構造 http://www.slideshare.net/ssuserf87701/2015gpgpu2-59179215 ・第3回　GPGPUプログラミング環境 http://www.slideshare.net/ssuserf87701/2015gpgpu3-59179255 ・第3回補足 GROUSEの利用方法 http://www.slideshare.net/ssuserf87701/2015gpgpu3-59183677 ・第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法） http://www.slideshare.net/ssuserf87701/2015gpgpu4-59179449 ・第5回　GPUのメモリ階層 http://www.slideshare.net/ssuserf87701/2015gpgpu5-59179536 ・第6回　パフォーマンス解析ツール http://www.slideshare.net/ssuserf87701/2015gpgpu6-59179577 ・第7回　総和計算 http://www.slideshare.net/ssuserf87701/2015gpgpu7-59179639 ・第8回　総和計算（高度な最適化） http://www.slideshare.net/ssuserf87701/2015gpgpu8-59179686 ・第9回　行列計算（行列－行列積） http://www.slideshare.net/ssuserf87701/2015gpgpu9-59179722 ・第10回　行列計算（行列－行列積の高度な最適化） http://www.slideshare.net/ssuserf87701/2015gpgpu10-59179759 ・第11回　画像処理 http://www.slideshare.net/ssuserf87701/2015gpgpu11-59179789 ・第12回　偏微分方程式の差分計算 http://www.slideshare.net/ssuserf87701/2015gpgpu12-59179972 ・第13回　多粒子の運動 http://www.slideshare.net/ssuserf87701/2015gpgpu13-59180018 ・第14回　N体問題 http://www.slideshare.net/ssuserf87701/2015gpgpu14-59180054 ・第15回　GPU最適化ライブラリ http://www.slideshare.net/ssuserf87701/2015gpgpu15-59180086 2015年度先端GPGPUシミュレーション工学特論 ・第1回　先端シミュレーションおよび産業界におけるGPUの役割 http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180313 2015年度GPGPU実践基礎工学 ・第1回　学際的分野における先端シミュレーション技術の歴史 http://www.slideshare.net/ssuserf87701/2015gpgpu1 講義には長岡技術科学大学のGPGPUシステム（GROUSE）を利用しています。 開発環境 CPU　Intel Xeon X5670 × 32 GPU　NVIDIA Tesla M2050（Fermi世代） × 64 CUDA 4.0（諸般の事情によりバージョンアップされていません） PGI Fortran 11.3

Embed presentation

Download as PDF, PPTX
第8回 総和計算（高度な最適化） 長岡技術科学大学 電気電子情報工学専攻 出川智啓
今回の内容 2015/06/03GPGPU実践プログラミング2  総和計算  CUDAによる総和計算の最適化  共有メモリの利用  バンクコンフリクトの解消  ストライドの変更  Warpの特性を活用したif分岐の排除  Templateの利用
リダクション（Reduction，換算） 2015/06/03GPGPU実践プログラミング3  配列の全要素から一つの値を抽出  総和，総積，最大値，最小値など  ベクトル和や移動平均，差分法とは処理が異なる  リダクションの特徴  データ参照が大域的  計算順序は交換可能  出力が一つ  出力は並列に計算できない  並列化に工夫が必要 sum a[i] ＋ ＋ ＋ ＋ ＋ ＋
総和計算の並列化 2015/06/03GPGPU実践プログラミング4  リダクションの並列性  並列性なし  i=0の処理が終了しないとi=1の処理ができない  リダクションの並列化  リダクションの特徴に適した並列化が必要  Parallel Reduction for(i=0;i<N;i++){ sum += idata[i]; }
総和計算の並列化 2015/06/03GPGPU実践プログラミング5  リダクションの並列化  演算順序の変更による並列性の確保  カスケード計算(associative fan‐in algorithm) sum a[i]  カスケード計算  加算の結合法則を利用  乗算や比較でも利用可能  配列要素数が2の冪乗以外では適用 に工夫が必要  変数に浮動小数を用いる場合は値が 一致しないことがある sum a[i] ＋ ＋ ＋ ＋ ＋ ＋ ＋
Parallel ReductionのGPU実装 2015/06/03GPGPU実践プログラミング6  Ver.0 1スレッド実行  Ver.1~1.2 複数スレッドを使ったカスケード計算  Ver.2 共有メモリによるキャッシュ利用  Ver.3~3.3 大きな入力データへの対応
Ver.2の問題点 2015/06/03GPGPU実践プログラミング7  部分和，総和の計算を行うスレッド番号が不連続  稼働するスレッド  グローバルメモリから共有メモリへのコピー 全スレッド  総和計算の1step目 スレッド番号が2の倍数と0  総和計算の2step目 スレッド番号が4の倍数と0  総和計算の3step目 スレッド番号が8の倍数と0...  CUDAのスレッド管理  32スレッドをWarpという単位で管理  同一Warpに属するスレッドが異なる処理を行うとbranch  divergenceが発生
Ver.2の改良 2015/06/03GPGPU実践プログラミング8  処理を行うスレッドの番号が連続になるよう設定  divergentが発生するWarpを減らす  全スレッドがグローバルメモリから共有メモリへデータを コピー  スレッド番号が小さい順にスレッドが処理を実行
総和の並列実行 2015/06/03GPGPU実践プログラミング9  スレッド番号が小さい順に スレッドが処理を実行  step 1ではスレッド番号 0~blockDim.x/2‐1 スレッド0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ Step 1 Step 2 Step 3 スレッド1 スレッド2 スレッド3
総和の並列実行 2015/06/03GPGPU実践プログラミング10  スレッド番号が小さいス レッドが処理を実行  step 1ではスレッド番号 0~blockDim.x/2‐1  step 2ではスレッド番号 0~blockDim.x/4‐1 スレッド0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ Step 1 Step 2 Step 3 スレッド1 スレッド2 スレッド3 スレッド0 スレッド1
総和の並列実行 2015/06/03GPGPU実践プログラミング11  スレッド番号が小さいス レッドが処理を実行  step 1ではスレッド番号 0~blockDim.x/2‐1  step 2ではスレッド番号 0~blockDim.x/4‐1  step 3ではスレッド番号 0~blockDim.x/8‐1 ... スレッド0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ Step 1 Step 2 Step 3 スレッド1 スレッド2 スレッド3 スレッド0 スレッド1 スレッド0
#include<stdio.h> #include<stdlib.h> #define N (512) #define Nbytes (N*sizeof(int)) #define NT (N) #define NB (N/NT) __global__ void reduction4(int *idata,int *odata){ //内容は2枚後のスライド } void init(int *idata){ //初期化の内容は同じなので省略 } GPUプログラム（Ver.4） 2015/06/03GPGPU実践プログラミング12 reduction4.cu
int main(){ int *idata,*odata;   //GPU用変数 idata:入力，odata:出力（=総和） int *host_idata,sum; //CPU用変数 host_idata:初期化用，sum:総和 cudaMalloc( (void **)&idata, Nbytes); cudaMalloc( (void **)&odata, sizeof(int)); //CPU側でデータを初期化してGPUへコピー host_idata = (int *)malloc(Nbytes); init(host_idata); cudaMemcpy(idata, host_idata,Nbytes, cudaMemcpyHostToDevice); free(host_idata); reduction4<<< NB, NT >>>(idata, odata); //GPUから総和の結果を受け取って画面表示 cudaMemcpy(&sum, odata, sizeof(int), cudaMemcpyDeviceToHost); printf("sum = %d¥n", sum); cudaFree(idata); cudaFree(odata); return 0; } GPUプログラム（Ver.4） 2015/06/03GPGPU実践プログラミング13 reduction4.cu
__global__ void reduction4(int *idata,int *odata){ int i = blockIdx.x*blockDim.x + threadIdx.x;//スレッドと配列要素の対応 int tx = threadIdx.x; //スレッド番号 int stride;  //”隣”の配列要素までの距離 int j; //各stepで総和計算を行うスレッドが //アクセスする配列要素番号 __shared__ volatile int s_idata[NT]; //共有メモリの宣言 s_idata[tx] = idata[i]; //グローバルメモリから共有メモリへデータをコピー __syncthreads(); //共有メモリのデータは全スレッドから参照されるので同期を取る for(stride = 1; stride <= blockDim.x/2; stride<<=1){ j = 2*stride * tx; //総和計算を行うスレッド番号とアクセスする配列要素の決定 if(j<blockDim.x){ s_idata[j] += s_idata[j+stride]; } __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } 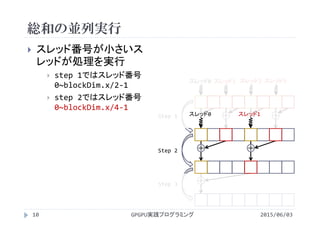GPUプログラム（Ver.4） 2015/06/03GPGPU実践プログラミング14 reduction4.cu
各Stepでの総和計算(Step 1) 2015/06/03GPGPU実践プログラミング15  処理を行うスレッドとアクセスする配列 要素を決定  連続なスレッドが2*stride間隔で配列にア クセス  スレッド0がs_idata[0(=2*1 * 0)]  スレッド1がs_idata[2(=2*1 * 1)]  スレッド2がs_idata[4(=2*1 * 2)]  スレッド3がs_idata[6(=2*1 * 3)]  jがblockDim.x(=配列要素数N)より小さく なるスレッドが「自身が読み込む配列要素i の値」と「隣の配列要素の値」を加算 ＋ ＋ ＋ ＋ ＋ ＋ ＋ stride が1の段 for(stride = 1; stride <= blockDim.x/2;  stride<<=1){ j = 2*stride * tx; if(j<blockDim.x){ s_idata[j]+=s_idata[j+stride]; } __syncthreads(); } スレッド0 スレッド1 スレッド2 スレッド3
各Stepでの総和計算(Step 2) 2015/06/03GPGPU実践プログラミング16  処理を行うスレッドとアクセスする配列 要素を決定  連続なスレッドが2*stride間隔で配列にア クセス  スレッド0がs_idata[0(=2*2 * 0)]  スレッド1がs_idata[4(=2*2 * 1)]  jがblockDim.x(=配列要素数N)より小さく なるスレッドが「自身が読み込む配列要素i の値」と「隣の配列要素の値」を加算 ＋ ＋ ＋ ＋ ＋ ＋ ＋ stride が2の段 for(stride = 1; stride <= blockDim.x/2;  stride<<=1){ j = 2*stride * tx; if(j<blockDim.x){ s_idata[j]+=s_idata[j+stride]; } __syncthreads(); } スレッド0 スレッド1
各Stepでの総和計算(Step 3) 2015/06/03GPGPU実践プログラミング17  処理を行うスレッドとアクセスする配列 要素を決定  連続なスレッドが2*stride間隔で配列にア クセス  スレッド0がs_idata[0(=2*4 * 0)]  jがblockDim.x(=配列要素数N)より小さく なるスレッドが「自身が読み込む配列要素i の値」と「隣の配列要素の値」を加算 ＋ ＋ ＋ ＋ ＋ ＋ ＋stride が4の段 スレッド0 for(stride = 1; stride <= blockDim.x/2;  stride<<=1){ j = 2*stride * tx; if(j<blockDim.x){ s_idata[j]+=s_idata[j+stride]; } __syncthreads(); }
各Stepでの総和計算(結果の書き出し) 2015/06/03GPGPU実践プログラミング18  スレッド0が総和を出力用変数odataに 書き込んで終了 ＋ ＋ ＋ ＋ ＋ ＋ ＋ if(tx==0) odata[blockIdx.x] = s_idata[0]; スレッド0
実行時間 2015/06/03GPGPU実践プログラミング カーネル N=512 N=1024 実行時間 [s] データ転送 [GB/s] 実行時間 [s] データ転送 [GB/s] 0 54.6 0.035 121 0.032 1 9.73 0.196 12.8 0.297 2 10.9 0.175 15.9 0.240 4 10.8 0.177 14.8 0.258 5 6 7 8 19
Ver.4の問題点 2015/06/03GPGPU実践プログラミング20  各スレッドが最初にアクセスする共有メモリが偶数  スレッド0がs_idata[0]，スレッド1がs_idata[2]，スレッド2が s_idata[4]...  2‐wayバンクコンフリクトが発生  l1_shared_bank_conflictをプロファイラで確認  l1_shared_bank_conflict=[465]  スレッド番号やアクセスする配列要素の位置がわかりにくい 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 12 8 0 1 2 3 16 14 4 4 5 6 7 32 16 0 8 9 10 11 48 17 6 12 13 14 15 64 19 2 16 17 18 19 80 20 8 20 21 22 23 96 22 4 24 25 26 27 11 2 24 0 28 29 30 31バンク番号 バンク コンフリクト
Ver.4の改良 2015/06/03GPGPU実践プログラミング21  加算するデータの順序を変更  Ver.4まで  stepが進む度にストライドが1, 2, 4, 8と増加  各スレッドはストライド×2の間隔で共有メモリへアクセス  改良版（Ver.5）  各スレッドが連続したメモリアドレスにアクセス  stepが進む度にストライドを8, 4, 2, 1と減少
ストライドを減少させる総和計算 2015/06/03GPGPU実践プログラミング22  Stepが進むとストライドが 減少  forループの初期条件と継 続条件が変化  step 1ではストライド4  step 2ではストライド2  step 3ではストライド1 ...  連続したスレッドが連続し たメモリアドレスにアクセス  スレッド番号と配列要素番 号の計算を排除 T0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ Step 1 Step 2 Step 3 T1 T2 T3
//カーネル以外はreduction4.cuと同じ __global__ void reduction5(int *idata,int *odata){ int i = blockIdx.x*blockDim.x + threadIdx.x;//スレッドと配列要素の対応 int tx = threadIdx.x; //スレッド番号 int stride;  //”隣”の配列要素までの距離 __shared__ volatile int s_idata[NT]; //共有メモリの宣言 s_idata[tx] = idata[i]; //グローバルメモリから共有メモリへデータをコピー __syncthreads(); //共有メモリのデータは全スレッドから参照されるので同期を取る //ストライドをblockDim.x/2からループ毎に1/2 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ //ストライドよりスレッド番号が小さいスレッドのみ計算に参加 s_idata[tx] += s_idata[tx+stride]; } __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } GPUプログラム（Ver.5） 2015/06/03GPGPU実践プログラミング23 reduction5.cu
各Stepでの総和計算(Step 1) 2015/06/03GPGPU実践プログラミング24  ストライドをblockDim.x/2(=配列要素 数/2)からループ毎に1/2倍に狭める  処理を行うスレッドとアクセスする配列 要素を決定  ストライドよりもスレッド番号が小さいスレッド  連続なスレッドが連続な配列要素にアクセス  スレッド0がs_idata[0]とs_idata[0+4]  スレッド1がs_idata[1]とs_idata[1+4]  スレッド2がs_idata[2]とs_idata[2+4]  スレッド3がs_idata[3]とs_idata[3+4] stride が4の段 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx]+=s_idata[tx+stride]; } __syncthreads(); } T0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ T1 T2 T3
＋ ＋ ＋ ＋ ＋ ＋ ＋ 各Stepでの総和計算(Step 2) 2015/06/03GPGPU実践プログラミング25  処理を行うスレッドとアクセスする配列 要素を決定  ストライドよりもスレッド番号が小さいスレッド  連続なスレッドが連続な配列要素にアクセス  スレッド0がs_idata[0]とs_idata[0+2]  スレッド1がs_idata[1]とs_idata[1+2] stride が2の段 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx]+=s_idata[tx+stride]; } __syncthreads(); } T0 T1
各Stepでの総和計算(Step 3) 2015/06/03GPGPU実践プログラミング26  処理を行うスレッドとアクセスする配列 要素を決定  ストライドよりもスレッド番号が小さいスレッド  連続なスレッドが連続な配列要素にアクセス  スレッド0がs_idata[0]とs_idata[0+1] stride が1の段 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx]+=s_idata[tx+stride]; } __syncthreads(); } ＋ ＋ ＋ ＋ ＋ ＋ ＋ T0
実行時間 2015/06/03GPGPU実践プログラミング カーネル N=512 N=1024 実行時間 [s] データ転送 [GB/s] 実行時間 [s] データ転送 [GB/s] 0 54.6 0.035 121 0.032 1 9.73 0.196 12.8 0.297 2 10.9 0.175 15.9 0.240 4 10.8 0.177 14.8 0.258 5 6.91  0.276 8.70 0.438 6 7 8 27
Ver.5の問題点と改良 2015/06/03GPGPU実践プログラミング28  1ブロック内のスレッドが実行する処理  グローバルメモリから共有メモリにデータをコピー（全スレッド）  総和計算（設定したスレッド数の半分）  1ブロック内のスレッド数を1/2に削減  1スレッドがグローバルメモリから2点のデータをコピー  コピーの際に加算を行い，共有メモリ使用量も1/2に削減  全スレッドが少なくとも1回は加算を実行
全スレッドを加算に参加させる総和計算 2015/06/03GPGPU実践プログラミング29  スレッド数を1/2に削減  共有メモリサイズも1/2  グローバルメモリから共有 メモリへのコピーと初回の 加算を同時に実行  ブロック数は変更無し  これまでの「1スレッドが 一つの配列要素にアクセ ス」という概念を発展  理解できれば脱初級者 T0 ＋ ＋ ＋ Step 1 Step 2 Step 3 T1 T2 T3 s_idata[i] idata[i] ＋ ＋ ＋ ＋ 共 有 メ モ リ グ ロ ー バ ル メ モ リ
1スレッドが2点以上計算する時の考え方 2015/06/03GPGPU実践プログラミング30  1スレッドが2点以上を計算する状況  配列サイズが大きすぎる  設定できるブロック数*スレッド数を超える  1スレッド1要素では計算できないので，2点以上計算  性能改善  1スレッドあたりの負荷を増加しつつ，1ブロックが利用する資源を節約  1スレッドがどのように複数の点を計算するか  ＝どのようにブロックとスレッドの数を設定するか  ＝どのようにスレッド番号と配列要素を対応させるか
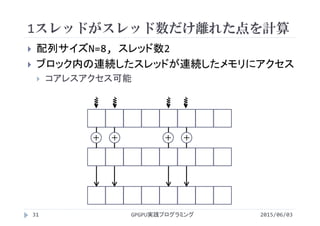
1スレッドがスレッド数だけ離れた点を計算 2015/06/03GPGPU実践プログラミング31  配列サイズN=8, スレッド数2  ブロック内の連続したスレッドが連続したメモリにアクセス  コアレスアクセス可能 ＋ ＋ ＋ ＋
1スレッドがスレッド数だけ離れた点を計算 2015/06/03GPGPU実践プログラミング32  配列サイズN=8, スレッド数2  ブロック内の連続したスレッドが連続したメモリにアクセス  コアレスアクセス可能 ＋ ＋ ＋ ＋
配列の要素番号iの計算  N=12, <<<3, 4>>>で実行 c[i] a[i] b[i] 0 1 2 3 0 1 ＋ ＋ ＋ ＋ ＋ ＋ 2 3 ＋ ＋ gridDim.x=3 blockDim.x=4 2015/06/03GPGPU実践プログラミング33 0 1 2 3 ＋ ＋ ＋ ＋ blockDim.x=4 blockDim.x=4 blockIdx.x=0 blockIdx.x=1 blockIdx.x=2 threadIdx.x= i=  0   1   2   3   4   5  6   7  8   9  10 11 = blockIdx.x*blockDim.x + threadIdx.x
配列の要素番号iの計算  N=12, <<<3, 2>>>で実行 2015/06/03GPGPU実践プログラミング34 c[i] a[i] b[i] 0 1 0 1 ＋ ＋ ＋ ＋ gridDim.x=3 blockDim.x=2 0 1 ＋ ＋ blockDim.x=2 blockDim.x=2 blockIdx.x=0 blockIdx.x=1 blockIdx.x=2 threadIdx.x= i=  0   1   2   3   4   5  6   7  8   9  10 11
配列の要素番号iの計算 2015/06/03GPGPU実践プログラミング35  threadIdx.xとiの対応  iの決定  配列サイズ=ブロックの数×1ブロックあたりのスレッドの数  配列サイズ=ブロックの数×1ブロックあたりのスレッドの数 ×1スレッドが計算する点の数 blockIdx.x 0 0 1 1 2 2 threadIdx.x 0 1 0 1 0 1 i 0 1 4 =4+0 5 =4+1 8 =8+0 9 =8+1 この影響をどのように式に書くか? blockIdx.x>0 でthreadIdx.x とiをどう対応さ せるか
配列の要素番号iの計算  1点目の計算 2015/06/03GPGPU実践プログラミング36 c[i] a[i] b[i] 0 1 0 1 ＋ ＋ ＋ ＋ gridDim.x=3 0 1 ＋ ＋ blockIdx.x=0 blockIdx.x=1 blockIdx.x=2 threadIdx.x= i=  0   1   2   3   4   5  6   7  8   9  10 11 = blockIdx.x*(blockDim.x*2) + threadIdx.x 1スレッドが計 算する点の数 blockDim.x=2 blockDim.x=2 blockDim.x=2
＋ ＋ ＋ ＋ ＋ 配列の要素番号iの計算  2点目の計算 2015/06/03GPGPU実践プログラミング37 c[i] a[i] b[i] 0 1 0 1 gridDim.x=3 0 1 blockIdx.x=0 blockIdx.x=1 blockIdx.x=2 threadIdx.x= ＋i=  0   1   2   3   4   5  6   7  8   9  10 11 = blockIdx.x*(blockDim.x*2) + threadIdx.x+2 1点目と2点目の間隔 =スレッド数 blockDim.x=2 blockDim.x=2 blockDim.x=2
#include<stdio.h> #include<stdlib.h> #define N (256) #define Nbytes (N*sizeof(int)) #define NT (N/2)    //スレッド数を半分に #define NB (N/NT/2) //スレッド数を半分にするとブロック数が増えてしまうので， //ブロック数を増やさないように調整 __global__ void reduction6(int *idata,int *odata){ //内容は後のスライド } void init(int *idata){ //初期化の内容は同じなので省略 } //main関数は変更無し GPUプログラム（Ver.6） 2015/06/03GPGPU実践プログラミング38 reduction6.cu
//#define NT (N/2) //#define NB (N/NT/2) __global__ void reduction4(int *idata,int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;//スレッドと配列要素の対応 int tx = threadIdx.x; //スレッド番号 int stride;  //”隣”の配列要素までの距離 __shared__ volatile int s_idata[NT]; //NTは定義の時点で1/2倍されている //グローバルメモリから共有メモリへデータをコピー．1スレッドが2点読み込んで加算 s_idata[tx] = idata[i] + idata[i+blockDim.x]; //blockDim.xは1スレッドが読み込む __syncthreads(); //1点目と2点目の間隔 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx] = s_idata[tx]+s_idata[tx+stride]; } __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } GPUプログラム（Ver.6） 2015/06/03GPGPU実践プログラミング39 reduction6.cu
各Stepでの総和計算(Step 1) 2015/06/03GPGPU実践プログラミング40  グローバルメモリから共有メモリへデー タをコピー  1スレッドが2点読み込んで加算  1点目と2点目の間隔はスレッド数(=NT=  blockDim.x)と等しい  スレッド0がidata[0]とidata[0+4]  スレッド1がidata[1]とidata[1+4]  スレッド2がidata[2]とidata[2+4]  スレッド3がidata[3]とidata[3+4] stride が4の段 __shared__ volatile int s_idata[NT]; s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); T0 ＋ ＋ ＋ ＋ ＋ ＋ ＋ T1 T2 T3 s_idata[i] idata[i]
＋ ＋ ＋ ＋ ＋ ＋ ＋ 各Stepでの総和計算(Step 2) 2015/06/03GPGPU実践プログラミング41  ストライドを1/2倍しながら，処理を実行 するスレッドを決定  ストライドよりもスレッド番号が小さいスレッド  連続なスレッドが連続な配列要素にアクセス  スレッド0がs_idata[0]とs_idata[0+2]  スレッド1がs_idata[1]とs_idata[1+2]  総和の計算はVer.5と同じ stride が2の段 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx]=s_idata[tx]+s_idata[tx+stride]; } __syncthreads(); } T0 T1
各Stepでの総和計算(Step 3) 2015/06/03GPGPU実践プログラミング42  ストライドを1/2倍しながら，処理を実行 するスレッドを決定  ストライドよりもスレッド番号が小さいスレッド  連続なスレッドが連続な配列要素にアクセス  スレッド0がs_idata[0]とs_idata[0+1]  総和の計算はVer.5と同じ stride が1の段 for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx]=s_idata[tx]+s_idata[tx+stride]; } __syncthreads(); } ＋ ＋ ＋ ＋ ＋ ＋ ＋ T0
実行時間 2015/06/03GPGPU実践プログラミング カーネル N=512 N=1024 実行時間 [s] データ転送 [GB/s] 実行時間 [s] データ転送 [GB/s] 0 54.6 0.035 121 0.032 1 9.73 0.196 12.8 0.297 2 10.9 0.175 15.9 0.240 4 10.8 0.177 14.8 0.258 5 6.91  0.276 8.70 0.438 6 6.40 0.298 7.07 0.540 7 8 43
Ver.6の問題点と改良 2015/06/03GPGPU実践プログラミング44  Warp内の各スレッドが異なる処理を実行  Stepが進むにつれて処理を行うスレッドが減少  Warp内でdivergentが発生  処理を行うスレッド数が32以下になった時点で処理を切替  スレッド数が32以下  スレッド番号が小さいスレッドで処理を実行  スレッド数が32以下の時は1 Warpのみが処理を実行  forループから抜け，32スレッドが行う処理をベタ書き  いくつかのスレッドが無駄な処理を実行  同一Warp内の32スレッドは協調して処理を実行  無駄な処理をしても処理速度は低下しない
Warp divergentを排除する総和計算 2015/06/03GPGPU実践プログラミング45  1 Warp内でif分岐しな いよう処理を記述  Reductionの段数が進行 すると，無駄な処理を行う スレッドが出現，増加  同一Warp内の32スレッドは 協調して処理を実行  無駄な処理をしても処理速 度は低下しない  最終的に必要となる結果 に影響はない ＋ ＋ ＋ ＋ ＋ ＋ ＋ 1Warpが2スレッド と仮定した場合 ＋
#include<stdio.h> #include<stdlib.h> #define N (256) #define Nbytes (N*sizeof(int)) #define NT (N/2)    //スレッド数を半分に #define NB (N/NT/2) //スレッド数を半分にするとブロック数が増えてしまうので， //ブロック数を増やさないように調整 #define smemSize ( (NT>32)*NT + (NT<=32)*(NT+NT/2) )//共有メモリの要素数を決定 __global__ void reduction7(int *idata,int *odata){ //内容は後のスライド } void init(int *idata){ //初期化の内容は同じなので省略 } //main関数は変更無し GPUプログラム（Ver.7） 2015/06/03GPGPU実践プログラミング46 reduction7.cu
__global__ void reduction7(int *idata,int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;//スレッドと配列要素の対応 int tx = threadIdx.x; //スレッド番号 int stride;  //”隣”の配列要素までの距離 //入力データの数に応じて必要な共有メモリサイズが変化 __shared__ volatile int s_idata[smemSize];  //グローバルメモリから共有メモリへデータをコピー．1スレッドが2点読み込んで加算 s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); //ストライドが32より大きい（=処理を実行するスレッドが32以上）場合にループ内の処理を実行 for(stride = blockDim.x/2; stride > 32; stride>>=1){ if(tx < stride){ s_idata[tx] = s_idata[tx]+s_idata[tx+stride]; } __syncthreads(); } 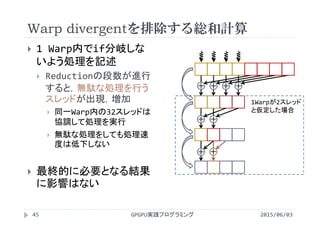GPUプログラム（Ver.7） 2015/06/03GPGPU実践プログラミング47 reduction7.cu
//処理を実行するスレッドが32（1 Warp内の0~31）になると処理を切替 //0~31スレッド全てが協調してif文内の処理を実行するため，__syncthreads();が不要 if(tx<32){ if(blockDim.x>=64) s_idata[tx] += s_idata[tx+32]; //if(blockDim.x>=??)は if(blockDim.x>=32) s_idata[tx] += s_idata[tx+16]; //入力データ数が64以下の条件 if(blockDim.x>=16) s_idata[tx] += s_idata[tx+ 8]; //で正しく結果を求めるために必要 if(blockDim.x>= 8) s_idata[tx] += s_idata[tx+ 4]; // if(blockDim.x>= 4) s_idata[tx] += s_idata[tx+ 2]; // if(blockDim.x>= 2) s_idata[tx] += s_idata[tx+ 1]; // } if(tx==0) odata[blockIdx.x] = s_idata[0]; } GPUプログラム（Ver.7） 2015/06/03GPGPU実践プログラミング48 reduction7.cu
1 Warp内での総和計算 2015/06/03GPGPU実践プログラミング49  スレッド数（=ストライド）が1 Warp以下 になるまでの処理はこれまでと同じ  1 Warp内で分岐せず，32スレッドが加 算を実行  計算を進行すると無意味な値が配列内に書 き込まれる  必要な値（部分和や総和）には影響しない  同期が不要  同期待ち時間が解消されて高速化? if(tx<32){ if(blockDim.x>=64) s_idata[tx]+=s_idata[tx+32]; if(blockDim.x>=32) s_idata[tx]+=s_idata[tx+16]; if(blockDim.x>=16) s_idata[tx]+=s_idata[tx+ 8]; if(blockDim.x>= 8) s_idata[tx]+=s_idata[tx+ 4]; if(blockDim.x>= 4) s_idata[tx]+=s_idata[tx+ 2]; if(blockDim.x>= 2) s_idata[tx]+=s_idata[tx+ 1]; } ＋ ＋ ＋ ＋ ＋ ＋ ＋ 1Warpが4スレッド と仮定した場合 ＋ ＋ ＋ ＋ ＋
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング50  入力する配列要素数によって共有メモリの取り方が変化  配列要素数が64より大きい（スレッド数が32より大きい）  2 Warp以上が総和計算に参加  共有メモリの要素数はスレッド数と同じ（配列要素数の1/2）  Ver.6までと同じ  配列要素数が64以下（スレッド数が32以下）  1 Warpのみが総和計算に参加  共有メモリの要素数はスレッド数×1.5  配列外参照を回避するため，共有メモリを大きめに確保
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング51  配列要素数が64より大きい（スレッド数が32より大きい）  2 Warp以上が総和計算に参加 ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋  1Warp8スレッド， N=32を想定  スレッド数16 （2Warp）  共有メモリの要 素数16 グローバルメモリから共有メモリへコピー+加算(2Warpが参加) (1Warpのみが総和計算) 32‐>1616‐>88‐>44‐>2
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング52  配列要素数が64より大きい（スレッド数が32より大きい）  2 Warp以上が総和計算に参加 ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋  1Warp8スレッド， N=32を想定  スレッド数16 （2Warp）  共有メモリの要 素数16 グローバルメモリから共有メモリへコピー+加算(2Warpが参加) (1Warpのみが総和計算) 無駄な計算に 伴って発生する メモリアクセス 32‐>1616‐>88‐>44‐>2
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング53  配列要素数が64以下（スレッド数が32[1warp]以下）  配列外参照を回避するため，共有メモリを大きめに確保 ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋  1Warp8スレッド， N=16を想定  スレッド数8 （1Warp）  共有メモリの要 素数8  Ver.6までと同 じように宣言す ると，配列外参 照が発生 グローバルメモリから共有メモリへ コピー+加算 16‐>88‐>44‐>2
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング54  配列要素数が64以下（スレッド数が32[1warp]以下）  配列外参照を回避するため，共有メモリを大きめに確保 ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋  1Warp8スレッド， N=16を想定  スレッド数8 （1Warp）  共有メモリの要 素数8  Ver.6までと同 じように宣言す ると，配列外参 照が発生 グローバルメモリから共有メモリへ コピー+加算 無駄な計算に 伴って発生する 配列外参照 16‐>88‐>44‐>2
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング55  配列要素数が64以下（スレッド数が32[1warp]以下）  配列外参照を回避するため，共有メモリを大きめに確保 ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋ ＋  1Warp8スレッド， N=16を想定  スレッド数8 （1Warp）  共有メモリの要 素数8+4  +4は配列外参 照に備えて余分 に確保される分  スレッド数の1/2 グローバルメモリから共有メモリへ コピー+加算 配列外参照に 備えて余分に 確保 16‐>88‐>44‐>2
共有メモリの要素数の決定 2015/06/03GPGPU実践プログラミング56  コンパイル時にどのように切り替えるか  配列要素数が64以下（スレッド数が32以下）  共有メモリの要素数はスレッド数×1.5  配列要素数が64より大きい（スレッド数が32より大きい）  共有メモリの要素数はスレッド数と同じ  比較演算子を利用  <, <=, >, >=, ==, !=  比較の結果が真なら1，偽なら0を返す（他言語では異なる） #define smemSize ( (NT>32)*NT + (NT<=32)*(NT+NT/2) ) //NT> 32のとき 1   *NT +     0   *(NT+NT/2) //NT<=32のとき 0   *NT +     1   *(NT+NT/2)
実行時間 2015/06/03GPGPU実践プログラミング カーネル N=512 N=1024 実行時間 [s] データ転送 [GB/s] 実行時間 [s] データ転送 [GB/s] 0 54.6 0.035 121 0.032 1 9.73 0.196 12.8 0.297 2 10.9 0.175 15.9 0.240 4 10.8 0.177 14.8 0.258 5 6.91  0.276 8.70 0.438 6 6.40 0.298 7.07 0.540 7 5.28 0.361 5.82 0.655 57
Ver.7の改良 2015/06/03GPGPU実践プログラミング58  forループ自体を削除  継続条件の判定も比較的大きな負荷の一つ  配列要素数が64以下のときはforループを使わず記述  配列サイズの変更に伴うif(blockDim.x>=??)も排除  C++の機能であるtemplateを利用することで実現  CUDAでもテンプレートを利用可能
template 2015/06/03GPGPU実践プログラミング59  コンパイル時にコードを生成する機能  テンプレート仮引数(パラメータ)を利用して処理を記述  テンプレート実引数の情報からコードを生成（実体化）  C言語の関数形式マクロの安全かつ高機能版 template<typename T> T add(T a, T b){ return a + b; } int main(void){ int ia=1,ib=2; float fa=1.0f,fb=2.0f; add<int>(ia,ib);   //typename Tが全てintになる add<float>(fa,fb); //typename Tが全てfloatになる return 0; }
template 2015/06/03GPGPU実践プログラミング60  型以外のテンプレートパラメータ  コンパイル時に値が決まる定数や式をテンプレート引数として 関数に渡すことが可能  型以外のテンプレートパラメータのみを指定することも可能 template<int smemSize> __global__ void reduction(int *idata, int *odata){ ... __shared__ volatile int s_idata[smemSize]; ... } int main(void){ ... reduction<64><<<NB, NT>>>(idata, odata); ... }
#include<stdio.h> #include<stdlib.h> #define N (1024) #define Nbytes (N*sizeof(int)) #define NT (N/2)    //スレッド数を半分に #define NB (N/NT/2) //スレッド数を半分にするとブロック数が増えてしまうので， //ブロック数を増やさないように調整 #define smemSize ( (NT>32)*NT + (NT<=32)*(NT+NT/2) )//共有メモリの要素数を決定 __global__ void reduction8(int *idata,int *odata){ //内容は後のスライド } void init(int *idata){ //初期化の内容は同じなので省略 } GPUプログラム（Ver.8） 2015/06/03GPGPU実践プログラミング61 reduction8.cu
//blockArraySize(1ブロックが処理する配列要素数=スレッド数の2倍)をテンプレートパラメータ //としてテンプレート関数を記述 template <unsigned int blockArraySize> __global__ void reduction8(int *idata, int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x;//スレッドと配列要素の対応 int tx = threadIdx.x; //スレッド番号 //入力データの数に応じて必要な共有メモリサイズが変化 __shared__ volatile int s_idata[smemSize];  if(blockArraySize == 1) return; //1ブロックあたりに処理する配列要素が1なら //関数を終了 //グローバルメモリから共有メモリへデータをコピー．1スレッドが2点読み込んで加算 s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); GPUプログラム（Ver.8） 2015/06/03GPGPU実践プログラミング62 reduction8.cu
if(blockArraySize >= 2048){ if(tx < 512){ s_idata[tx] += s_idata[tx+512];} __syncthreads(); } if(blockArraySize >= 1024){ if(tx < 256){ s_idata[tx] += s_idata[tx+256];} __syncthreads(); } if(blockArraySize >=  512){ if(tx < 128){ s_idata[tx] += s_idata[tx+128];} __syncthreads(); } if(blockArraySize >=  256){ if(tx <  64){ s_idata[tx] += s_idata[tx+ 64];} __syncthreads(); } if(tx<32){ if(blockArraySize >= 128) s_idata[tx] += s_idata[tx+32]; if(blockArraySize >=  64) s_idata[tx] += s_idata[tx+16]; if(blockArraySize >=  32) s_idata[tx] += s_idata[tx+ 8]; if(blockArraySize >=  16) s_idata[tx] += s_idata[tx+ 4]; if(blockArraySize >=   8) s_idata[tx] += s_idata[tx+ 2]; if(blockArraySize >=   4) s_idata[tx] += s_idata[tx+ 1]; } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } GPUプログラム（Ver.8） 2015/06/03GPGPU実践プログラミング63 reduction8.cu blockArraySizeはコンパイル時に 確定するため，if文は最適化される
int main(){ int *idata,*odata;   //GPU用変数 idata:入力，odata:出力（=総和） int *host_idata,sum; //CPU用変数 host_idata:初期化用，sum:総和 cudaMalloc( (void **)&idata, Nbytes); cudaMalloc( (void **)&odata, sizeof(int)); //CPU側でデータを初期化してGPUへコピー host_idata = (int *)malloc(Nbytes); init(host_idata); cudaMemcpy(idata, host_idata,Nbytes, cudaMemcpyHostToDevice); free(host_idata); reduction8<N><<< NB, NT >>>(idata, odata); //GPUから総和の結果を受け取って画面表示 cudaMemcpy(&sum, odata, sizeof(int), cudaMemcpyDeviceToHost); printf("sum = %d¥n", sum); cudaFree(idata); cudaFree(odata); return 0; } GPUプログラム（Ver.8） 2015/06/03GPGPU実践プログラミング64 reduction8.cu
カーネル実体化の流れ 2015/06/03GPGPU実践プログラミング65  定数マクロ（#define）でNの値を決定  #define N 1024  プリプロセッサがカーネルの呼出を書き換え  reduction8<N><<< NB, NT >>>(idata, odata);  reduction8<1024><<< 1, 512 >>>(idata, odata);  テンプレートパラメータが定まるのでカーネルを最適化  if(blockArraySize >= 2048){}は絶対に実行される事 がないので消去  それ以降のif文は全て成立  if文だけを消して処理を残す
__shared__ volatile int s_idata[512];  s_idata[i] = idata[i] + idata[i+blockDim.x];  //1024‐>512 __syncthreads(); if(tx < 256){ s_idata[tx] += s_idata[tx+256];} __syncthreads(); //512‐>256 if(tx < 128){ s_idata[tx] += s_idata[tx+128];} __syncthreads(); //256‐>128 if(tx <  64){ s_idata[tx] += s_idata[tx+ 64];} __syncthreads(); //128‐> 64 if(tx<32){ s_idata[tx] += s_idata[tx+32]; // 64‐> 32 s_idata[tx] += s_idata[tx+16]; // 32‐> 16 s_idata[tx] += s_idata[tx+ 8]; // 16‐>  8 s_idata[tx] += s_idata[tx+ 4]; //  8‐>  4 s_idata[tx] += s_idata[tx+ 2]; //  4‐>  2 s_idata[tx] += s_idata[tx+ 1]; //  2‐>  1 } if(tx==0) odata[0] = s_idata[tx]; 実体化されたカーネル（あくまで予想） 2015/06/03GPGPU実践プログラミング66
実行時間 2015/06/03GPGPU実践プログラミング カーネル N=512 N=1024 実行時間 [s] データ転送 [GB/s] 実行時間 [s] データ転送 [GB/s] 0 54.6 0.035 121 0.032 1 9.73 0.196 12.8 0.297 2 10.9 0.175 15.9 0.240 4 10.8 0.177 14.8 0.258 5 6.91  0.276 8.70 0.438 6 6.40 0.298 7.07 0.540 7 5.28 0.361 5.82 0.655 8 5.15 0.370 5.60 0.681 67
バージョン8の問題点と改良 2015/06/03GPGPU実践プログラミング68  配列要素数が2048以下  コンパイル時にテンプレートパラメータを確定  入力データ数が変わると対処不可能  部分和→総和だけなら対応可能  Ver.3.3のように複数回部分和を計算する条件では対応が 困難  共有メモリサイズが固定  switch文を利用して，取り得るテンプレートパラメータを 全て列挙  externを利用
#include<stdio.h> #include<stdlib.h> #define N (1024) #define Nbytes (N*sizeof(int)) #define NPB (512) //1ブロックが部分和を計算する配列要素数(Number of Points per Block) #define NT  (NPB/2) //1ブロックあたりのスレッド数 #define NB  (N/NPB) //ブロック数 //関数形式マクロで共有メモリサイズを決定 #define smemSize(x) ( ((x)>32)*x + ((x)<=32)*((x)+(x)/2) ) template <unsigned int blockArraySize> __global__ void reduction9(int *idata,int *odata){ //共有メモリの宣言以外，内容はVer.8と同じなので省略 __shared__ volatile int s_idata[smemSize(blockArraySize/2)]; } void init(int *idata){ //初期化の内容は同じなので省略 } GPUプログラム（Ver.9） 2015/06/03GPGPU実践プログラミング69 reduction9.cu
int main(){ int *idata,*odata;   //GPU用変数 idata:入力，odata:出力（=総和） int *host_idata,sum; //CPU用変数 host_idata:初期化用，sum:総和 cudaMalloc( (void **)&idata, Nbytes); cudaMalloc( (void **)&odata, NB*sizeof(int)); //CPU側でデータを初期化してGPUへコピー //...省略... reduction9<NPB><<< NB, NT   >>>(idata, odata);//各ブロックで部分和を計算 if(NB>1) reduction9<NB ><<<  1, NB/2 >>>(odata, odata);//部分和から総和を計算 //GPUから総和の結果を受け取って画面表示 cudaMemcpy(&sum, odata, sizeof(int), cudaMemcpyDeviceToHost); printf("sum = %d¥n", sum); cudaFree(idata); cudaFree(odata); return 0; } GPUプログラム（Ver.9） 2015/06/03GPGPU実践プログラミング70 reduction9.cu
関数形式マクロ 2015/06/03GPGPU実践プログラミング71  関数形式マクロ  関数のように引数を持ち，引数を使った処理を記述  プリプロセッサがコンパイル時に定義文を展開  #define square(x) ((x)*(x))  プログラム中のsquare(2)が定義式(2)*(2)に置き換えられる  演算を記述すると予期せぬ処理が行われる  square(++i) => (++i)*(++i)  iに1を加えて2乗したいのに，iに2が加えられて2乗が計算される  定数マクロ  文字列の並びを他の文字列に置き換え  #define N 1024  #define TYPE int
Switch文によるカーネル呼出の列挙 2015/06/03GPGPU実践プログラミング72  1ブロックあたりのスレッド数の上限1024  1ブロックが処理する配列要素数はスレッド数×2  配列要素数を2の冪乗に限定 reduction9.cu switch(numThread){ //numBlock, numThread, smemSizeはint型変数 case 1024: reduction9<1024*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  512: reduction9< 512*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  256: reduction9< 256*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  128: reduction9< 128*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case .... }
#include<stdio.h> #include<stdlib.h> #define N (1024) #define Nbytes (N*sizeof(int)) #define NPB (512) //1ブロックが部分和を計算する配列要素数(Number of Points per Block) #define NT  (NPB/2) //1ブロックあたりのスレッド数 #define NB  (N/NPB) //ブロック数 template <unsigned int blockArraySize> __global__ void reduction9(int *idata,int *odata){ //共有メモリの宣言以外，内容はVer.8と同じなので省略 extern __shared__ volatile int s_idata[]; } void reduction(int *idata, int *odata, int numBlock, int numThread){ //内容は2枚後のスライド } void init(int *idata){ //初期化の内容は同じなので省略 } GPUプログラム（Ver.9.1） 2015/06/03GPGPU実践プログラミング73 reduction9switch.cu
int main(){ int *idata,*odata;   //GPU用変数 idata:入力，odata:出力（=総和） int *host_idata,sum; //CPU用変数 host_idata:初期化用，sum:総和 cudaMalloc( (void **)&idata, Nbytes); cudaMalloc( (void **)&odata, NB*sizeof(int)); //CPU側でデータを初期化してGPUへコピー //...省略... reduction(idata, odata, NB, NT  );//各ブロックで部分和を計算 if(NB>1) reduction(odata, odata,  1, NB/2);//部分和から総和を計算 //GPUから総和の結果を受け取って画面表示 cudaMemcpy(&sum, odata, sizeof(int), cudaMemcpyDeviceToHost); printf("sum = %d¥n", sum); cudaFree(idata); cudaFree(odata); return 0; } GPUプログラム（Ver.9.1） 2015/06/03GPGPU実践プログラミング74 reduction9switch.cu
void reduction(int *idata, int *odata, int numBlock, int numThread){ int smemSize = sizeof(int) * numThread; if(numThread<=32) smemSize += sizeof(int) * numThread/2; switch(numThread){ //numBlock, numThread, smemSizeはint型変数 case 1024: reduction9<1024*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  512: reduction9< 512*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  256: reduction9< 256*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  128: reduction9< 128*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  64: reduction9<  64*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; GPUプログラム（Ver.9.1） 2015/06/03GPGPU実践プログラミング75 reduction9switch.cu
case   32: reduction9<  32*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case   16: reduction9<  16*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case   8: reduction9<  8*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case  4: reduction9< 4*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case    2: reduction9<  2*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; case   1: reduction9<  1*2><<<numBlock, numThread, smemSize>>>(idata, odata); break; default : printf("configuration error¥n"); } GPUプログラム（Ver.9.1） 2015/06/03GPGPU実践プログラミング76 reduction9switch.cu
実行時間 2015/06/03GPGPU実践プログラミング  入力データの個数N = 8192  1ブロックあたりのスレッド数NT=256 カーネル 実行時間 [s] データ転送[GB/s] 3.2 16.3 1.88 9.1 7.81 3.92 77
#include<stdio.h> #include<stdlib.h> #define N (1024*1024*8) #define Nbytes ((unsigned int)N*sizeof(int)) #include"kernel3.cu" //#include"kernel4.cu" //#include"kernel5.cu" //#include"kernel6.cu" //#include"kernel7.cu" //#include"kernel8.cu" //#include"kernel9.cu" void init(int *idata){//初期化 int i; for(i=0;i<N;i++){ idata[i] = 1; } } 大きな配列の総和 2015/06/03GPGPU実践プログラミング  Ver.3.4との組合せ 78 reduction.cu
int main(){ int *idata; int *host_idata; cudaMalloc( (void **)&idata, Nbytes); host_idata = (int *)malloc(Nbytes); init(host_idata); cudaMemcpy(idata, host_idata,Nbytes, cudaMemcpyHostToDevice); free(host_idata); //関数reduction内でカーネルreduction_kernelを複数回起動 //必要なパラメータも含めてkernel?.cuで定義 printf("array size = %d, sum = %d¥n", N, reduction(idata)); cudaFree(idata); return 0; } 大きな配列の総和 2015/06/03GPGPU実践プログラミング79 reduction.cu
//‐‐‐‐‐‐パラメータの定義‐‐‐‐‐‐// #define NT ... #define NB ... //‐‐‐‐‐‐カーネルの定義‐‐‐‐‐‐// __global__ void reduction_kernel(int *idata, int *odata){ } //‐‐‐‐‐‐カーネルを呼び出して総和を計算する関数の定義‐‐‐‐‐‐// int reduction(int *idata){ return result; } 大きな配列の総和 2015/06/03GPGPU実践プログラミング80 kernel?.cu
#define NT (256) #define NB (N/NT) __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*blockDim.x + threadIdx.x; int tx = threadIdx.x; int stride; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i]; __syncthreads(); for(stride = 1; stride <= blockDim.x/2; stride<<=1){ if(tx%(2*stride) == 0){ s_idata[tx] = s_idata[tx]+s_idata[tx+stride]; }   __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } kernel3 2015/06/03GPGPU実践プログラミング81 kernel3.cu スレッド ：不連続 ストライド：ステップ毎に増加
#define NT (256) #define NB (N/NT) __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*blockDim.x + threadIdx.x; int tx = threadIdx.x; int j; int stride; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i]; __syncthreads(); for(stride = 1; stride <= blockDim.x/2; stride<<=1){ j = 2*stride * tx; if(j < blockDim.x){ s_idata[j] = s_idata[j]+s_idata[j+stride]; }   __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } kernel4 2015/06/03GPGPU実践プログラミング82 kernel4.cu スレッド ：小さい順に連続 ストライド：ステップ毎に増加
#define NT (256) #define NB (N/NT) __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*blockDim.x + threadIdx.x; int tx = threadIdx.x; int stride; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i]; __syncthreads(); for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx] = s_idata[tx]+s_idata[tx+stride]; } __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[0]; } kernel5 2015/06/03GPGPU実践プログラミング83 kernel5.cu スレッド ：小さい順に連続 ストライド：ステップ毎に減少
int reduction(int *idata){ int numBlock, numThread, smemSize; int *odata; int result; numThread = NT; smemSize = numThread*sizeof(int); numBlock = NB; cudaMalloc( (void **)&odata,  numBlock*sizeof(int)); reduction_kernel<<< numBlock, numThread,  smemSize>>>(idata, odata); while(numBlock>NT){ numBlock /= NT; reduction_kernel<<< numBlock, numThread, smemSize>>>(odata, odata); } numThread = numBlock; smemSize = numThread*sizeof(int); numBlock = 1; if(numThread>1) reduction_kernel<<< numBlock, numThread,  smemSize>>>(odata, odata); cudaMemcpy(&result, &odata[0],  sizeof(int), cudaMemcpyDeviceToHost); cudaFree(odata); return result; } kernel3,4,5 2015/06/03GPGPU実践プログラミング84 kernel[3‐5].cu Ver.3.４から変更無し
#define NPB (512) #define NT (NPB/2) #define NB (N/NPB) __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x; int tx = threadIdx.x; int stride; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); for(stride = blockDim.x/2; stride >= 1; stride>>=1){ if(tx < stride){ s_idata[tx] = s_idata[tx]+s_idata[tx+stride]; }   __syncthreads(); } if(tx==0) odata[blockIdx.x] = s_idata[0]; } kernel6 2015/06/03GPGPU実践プログラミング85 kernel6.cu +スレッド数を1/2に削減スレッド ：小さい順に連続 ストライド：ステップ毎に増加
int reduction(int *idata){ int numBlock, numThread, smemSize; int *odata; int result; numThread = NT; smemSize = numThread*sizeof(int); numBlock = NB; cudaMalloc( (void **)&odata,  numBlock*sizeof(int)); reduction_kernel<<< numBlock, numThread, smemSize>>>(idata, odata); while(numBlock>NPB){ numBlock /= NPB; reduction_kernel<<< numBlock, numThread,  smemSize>>>(odata, odata); } numThread = numBlock/2; smemSize = numThread*sizeof(int); numBlock = 1; if(numThread>1) reduction_kernel<<< numBlock, numThread,  smemSize>>>(odata, odata); cudaMemcpy(&result, &odata[0], sizeof(int), cudaMemcpyDeviceToHost); cudaFree(odata); return result; } kernel6 2015/06/03GPGPU実践プログラミング86 kernel6.cu スレッド数と1ブロックが処理する配列要素数を区別
#define NPB (512) #define NT (NPB/2) #define NB (N/NPB) __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x; int tx = threadIdx.x; int stride; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); for(stride = blockDim.x/2; stride > 32; stride>>=1){ if(tx < stride){ s_idata[tx] += s_idata[tx+stride]; }   __syncthreads(); } kernel7 2015/06/03GPGPU実践プログラミング87 kernel7.cu +Warp内の処理を展開 スレッド ：小さい順に連続 ストライド：ステップ毎に増加 +スレッド数を1/2に削減
if(tx<32){ if(blockDim.x>=64)s_idata[tx] += s_idata[tx+32]; if(blockDim.x>=32)s_idata[tx] += s_idata[tx+16]; if(blockDim.x>=16)s_idata[tx] += s_idata[tx+ 8]; if(blockDim.x>= 8)s_idata[tx] += s_idata[tx+ 4]; if(blockDim.x>= 4)s_idata[tx] += s_idata[tx+ 2]; if(blockDim.x>= 2)s_idata[tx] += s_idata[tx+ 1]; } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } kernel7 2015/06/03GPGPU実践プログラミング88 kernel7.cu
int reduction(int *idata){ int numBlock, numThread, smemSize; int *odata; int result; numThread = NT; smemSize = numThread*sizeof(int); if(numThread<=32) smemSize += (numThread/2)*sizeof(int); numBlock = NB; cudaMalloc( (void **)&odata,  numBlock*sizeof(int)); reduction_kernel<<< numBlock, numThread,  smemSize>>>(idata, odata); while(numBlock>NPB){ numBlock /= NPB; reduction_kernel<<< numBlock, numThread,  smemSize>>>(odata, odata); } numThread = numBlock/2; smemSize = numThread*sizeof(int); if(numThread<=32) smemSize += (numThread/2)*sizeof(int); numBlock = 1; if(numThread>1) reduction_kernel<<< numBlock, numThread,  smemSize>>>(odata, odata); cudaMemcpy(&result, &odata[0],  sizeof(int), cudaMemcpyDeviceToHost); cudaFree(odata); return result; } kernel7 2015/06/03GPGPU実践プログラミング89 kernel7.cu スレッド数に応じて共有メモリ要素数を変更
#define NPB (512) #define NT (NPB/2) #define NB (N/NPB) template <unsigned int blockArraySize> __global__ void reduction_kernel(int *idata, int *odata){ int i = blockIdx.x*(blockDim.x*2) + threadIdx.x; int tx = threadIdx.x; extern __shared__ volatile int s_idata[]; s_idata[tx] = idata[i] + idata[i+blockDim.x]; __syncthreads(); kernel8,9 2015/06/03GPGPU実践プログラミング90 kernel[8‐9].cu +template による展開+Warp内の処理を展開 スレッド ：小さい順に連続 ストライド：ステップ毎に増加 +スレッド数を1/2に削減
if(blockArraySize >= 2048){ if(tx < 512){ s_idata[tx] += s_idata[tx+512];} __syncthreads(); } if(blockArraySize >= 1024){ if(tx < 256){ s_idata[tx] += s_idata[tx+256];} __syncthreads(); } if(blockArraySize >=  512){ if(tx < 128){ s_idata[tx] += s_idata[tx+128];} __syncthreads(); } if(blockArraySize >=  256){ if(tx <  64){ s_idata[tx] += s_idata[tx+ 64];} __syncthreads(); } if(tx<32){ if(blockArraySize >= 128)s_idata[tx] += s_idata[tx+32]; if(blockArraySize >=  64)s_idata[tx] += s_idata[tx+16]; if(blockArraySize >=  32)s_idata[tx] += s_idata[tx+ 8]; if(blockArraySize >=  16)s_idata[tx] += s_idata[tx+ 4]; if(blockArraySize >=   8)s_idata[tx] += s_idata[tx+ 2]; if(blockArraySize >=   4)s_idata[tx] += s_idata[tx+ 1]; } if(tx==0) odata[blockIdx.x] = s_idata[tx]; } kernel8,9 2015/06/03GPGPU実践プログラミング91 kernel[8‐9].cu
int reduction(int *idata){ int numBlock, numThread, smemSize; int *odata; int result; numThread = NT; if(numThread<=32) smemSize += (numThread/2)*sizeof(int); numBlock = NB; cudaMalloc( (void **)&odata,  numBlock*sizeof(int)); reduction_kernel<NPB><<< numBlock, numThread,  smemSize>>>(idata, odata); while(numBlock>NPB){ numBlock /= NPB; reduction_kernel<NPB><<< numBlock,  numThread, smemSize>>>(odata, odata); } numThread = numBlock/2; smemSize = numThread*sizeof(int); if(numThread<=32) smemSize += (numThread/2)*sizeof(int); numBlock = 1; if(numThread>1) //数字を何らかの方法で確定する必要がある reduction_kernel<32><<< numBlock, numThread,  smemSize>>>(odata, odata); cudaMemcpy(&result, &odata[0],  sizeof(int), cudaMemcpyDeviceToHost); cudaFree(odata); return result; } kernel8 2015/06/03GPGPU実践プログラミング92 kernel8.cu templateパラメータの記述（最終ステップのパラメータを 何らかの方法で確定する必要がある）
int reduction(int *idata){ int numBlock, numThread; int *odata; int result; numThread = NT; numBlock = NB; cudaMalloc( (void **)&odata, numBlock*sizeof(int)); invokeReductionKernel(idata, odata,  numBlock, numThread); while(numBlock>NPB){ numBlock /= NPB; invokeReductionKernel(odata, odata, numBlock, numThread); } numThread = numBlock/2; numBlock = 1; if(numThread>1) invokeReductionKernel(odata, odata,  numBlock, numThread); cudaMemcpy(&result, &odata[0],  sizeof(int), cudaMemcpyDeviceToHost); cudaFree(odata); return result; } kernel9 2015/06/03GPGPU実践プログラミング93 kernel9.cu switch文によるtemplateパラメータの列挙 （新たに関数を一つ導入）
void invokeReductionKernel(int *idata, int *odata, int numBlock, int numThread){ int smemSize = sizeof(idata[0])*numThread; if(numThread<=32) smemSize += sizeof(idata[0])*numThread/2; switch(numThread){ case 1024: reduction_kernel<1024*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case 512: reduction_kernel< 512*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case 256: reduction_kernel< 256*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case 128: reduction_kernel< 128*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case  64: reduction_kernel<  64*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case  32: reduction_kernel<  32*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; kernel9 2015/06/03GPGPU実践プログラミング94 kernel9.cu スレッド数に応じて適切なtemplateパラメータを選択し， カーネルを起動する関数
case  16: reduction_kernel<  16*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case   8: reduction_kernel<   8*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case   4: reduction_kernel<   4*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case   2: reduction_kernel<   2*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; case   1: reduction_kernel<   1*2><<< numBlock, numThread , smemSize >>>(idata, odata); break; default : printf("configuration error : number of threads per block¥n"); } } kernel9 2015/06/03GPGPU実践プログラミング95 kernel9.cu スレッド数に応じて適切なtemplateパラメータを選択し， カーネルを起動する関数
実行時間 2015/06/03GPGPU実践プログラミング  配列要素数N=223  1ブロックあたりのスレッド数 256  理論ピークバンド幅 148 GB/s カーネル 実行時間 [s] データ転送[GB/s] 3 474×10 6.59 4 248×10 12.6 5 183×10 17.1 6 939 33.3 7 706 44.3 8 519 60.2 9 515 60.7 96 ×1.91 ×1.36 ×1.95 ×1.33 ×1.36 高速化

More Related Content

PDF
2015年度GPGPU実践プログラミング　第7回　総和計算
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第5回　GPUのメモリ階層の詳細 （様々なメモリの利用）
by智啓 出川
 
PDF
いまさら聞けない！CUDA高速化入門
byFixstars Corporation
 
PDF
2015年度GPGPU実践基礎工学　第2回　GPGPUの歴史と応用例
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第6回　パフォーマンス解析ツール
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第5回　GPUのメモリ階層
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第4回　GPUのメモリ階層の詳細 （共有メモリ）
by智啓 出川
 
PDF
Layer Normalization@NIPS+読み会・関西
byKeigo Nishida
 
2015年度GPGPU実践プログラミング　第7回　総和計算
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第5回　GPUのメモリ階層の詳細 （様々なメモリの利用）
by智啓 出川
 
いまさら聞けない！CUDA高速化入門
byFixstars Corporation
 
2015年度GPGPU実践基礎工学　第2回　GPGPUの歴史と応用例
by智啓 出川
 
2015年度GPGPU実践プログラミング　第6回　パフォーマンス解析ツール
by智啓 出川
 
2015年度GPGPU実践プログラミング　第5回　GPUのメモリ階層
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第4回　GPUのメモリ階層の詳細 （共有メモリ）
by智啓 出川
 
Layer Normalization@NIPS+読み会・関西
byKeigo Nishida
 

What's hot

PDF
プログラムを高速化する話Ⅱ 〜GPGPU編〜
by京大 マイコンクラブ
 
PDF
CUDAプログラミング入門
byNVIDIA Japan
 
PDF
2015年度GPGPU実践プログラミング　第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法）
by智啓 出川
 
PDF
Ultra96ボードでYOLOを高速化
byHiroyuki Okuhata
 
PDF
1076: CUDAデバッグ・プロファイリング入門
byNVIDIA Japan
 
PDF
GPGPU Seminar (GPU Accelerated Libraries, 3 of 3, Thrust)
by智啓 出川
 
PPTX
研究者のための Python による FPGA 入門
byryos36
 
PDF
中３女子でもわかる constexpr
byGenya Murakami
 
PDF
はじめようGit
bytechscore
 
PDF
Binary indexed tree
byHCPC: 北海道大学競技プログラミングサークル
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第9回　偏微分方程式の差分計算 （移流方程式）
by智啓 出川
 
PDF
第1回 配信講義　計算科学技術特論A （2021）
byRCCSRENKEI
 
PPTX
DockerコンテナでGitを使う
byKazuhiro Suga
 
PDF
PEGで構文解析をする
byjiro4989
 
PPTX
画像処理ライブラリ OpenCV で 出来ること・出来ないこと
byNorishige Fukushima
 
PDF
2015年度GPGPU実践プログラミング　第10回　行列計算（行列－行列積の高度な最適化）
by智啓 出川
 
PPTX
【論文紹介】How Powerful are Graph Neural Networks?
byMasanao Ochi
 
PDF
2015年度GPGPU実践基礎工学　第13回　GPUのメモリ階層
by智啓 出川
 
PDF
Unityティーチャートレーニングデイ -認定プログラマー編-
byUnity Technologies Japan K.K.
 
PPTX
Deep Learningのための専用プロセッサ「MN-Core」の開発と活用（2022/10/19東大大学院「 融合情報学特別講義Ⅲ」）
byPreferred Networks
 
プログラムを高速化する話Ⅱ 〜GPGPU編〜
by京大 マイコンクラブ
 
CUDAプログラミング入門
byNVIDIA Japan
 
2015年度GPGPU実践プログラミング　第4回　GPUでの並列プログラミング（ベクトル和，移動平均，差分法）
by智啓 出川
 
Ultra96ボードでYOLOを高速化
byHiroyuki Okuhata
 
1076: CUDAデバッグ・プロファイリング入門
byNVIDIA Japan
 
GPGPU Seminar (GPU Accelerated Libraries, 3 of 3, Thrust)
by智啓 出川
 
研究者のための Python による FPGA 入門
byryos36
 
中３女子でもわかる constexpr
byGenya Murakami
 
はじめようGit
bytechscore
 
Binary indexed tree
byHCPC: 北海道大学競技プログラミングサークル
 
2015年度先端GPGPUシミュレーション工学特論　第9回　偏微分方程式の差分計算 （移流方程式）
by智啓 出川
 
第1回 配信講義　計算科学技術特論A （2021）
byRCCSRENKEI
 
DockerコンテナでGitを使う
byKazuhiro Suga
 
PEGで構文解析をする
byjiro4989
 
画像処理ライブラリ OpenCV で 出来ること・出来ないこと
byNorishige Fukushima
 
2015年度GPGPU実践プログラミング　第10回　行列計算（行列－行列積の高度な最適化）
by智啓 出川
 
【論文紹介】How Powerful are Graph Neural Networks?
byMasanao Ochi
 
2015年度GPGPU実践基礎工学　第13回　GPUのメモリ階層
by智啓 出川
 
Unityティーチャートレーニングデイ -認定プログラマー編-
byUnity Technologies Japan K.K.
 
Deep Learningのための専用プロセッサ「MN-Core」の開発と活用（2022/10/19東大大学院「 融合情報学特別講義Ⅲ」）
byPreferred Networks
 

Viewers also liked

PDF
2015年度GPGPU実践プログラミング　第14回　N体問題
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第4回　CPUのアーキテクチャ
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第11回　画像処理
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第13回　多粒子の運動
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第1回　学際的分野における先端シミュレーション技術の歴史
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第2回　GPUのアーキテクチャとプログラム構造
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第1回　GPGPUの歴史と応用例
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第3回　GPUクラスタ上でのプログラミング（CUDA）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第9回　行列計算（行列－行列積）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第12回　偏微分方程式の差分計算
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第6回　ソフトウェアによるCPUの高速化技術
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第7回　シングルコアとマルチコア
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第9回補足　GROUSEの利用方法
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第12回　GPUによる画像処理
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第5回　ハードウェアによるCPUの高速化技術
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第15回　GPU最適化ライブラリ
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第8回　並列計算の概念 （プロセスとスレッド）
by智啓 出川
 
PDF
2015年度GPGPU実践プログラミング　第3回　GPGPUプログラミング環境
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第11回　GPUでの並列 プログラミング（ベクトル和）
by智啓 出川
 
PDF
2015年度GPGPU実践基礎工学　第9回　GPUのアーキテクチャ
by智啓 出川
 
2015年度GPGPU実践プログラミング　第14回　N体問題
by智啓 出川
 
2015年度GPGPU実践基礎工学　第4回　CPUのアーキテクチャ
by智啓 出川
 
2015年度GPGPU実践プログラミング　第11回　画像処理
by智啓 出川
 
2015年度GPGPU実践プログラミング　第13回　多粒子の運動
by智啓 出川
 
2015年度GPGPU実践基礎工学　第1回　学際的分野における先端シミュレーション技術の歴史
by智啓 出川
 
2015年度GPGPU実践プログラミング　第2回　GPUのアーキテクチャとプログラム構造
by智啓 出川
 
2015年度GPGPU実践プログラミング　第1回　GPGPUの歴史と応用例
by智啓 出川
 
2015年度GPGPU実践基礎工学　第3回　GPUクラスタ上でのプログラミング（CUDA）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第9回　行列計算（行列－行列積）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第12回　偏微分方程式の差分計算
by智啓 出川
 
2015年度GPGPU実践基礎工学　第6回　ソフトウェアによるCPUの高速化技術
by智啓 出川
 
2015年度GPGPU実践基礎工学　第7回　シングルコアとマルチコア
by智啓 出川
 
2015年度GPGPU実践基礎工学　第9回補足　GROUSEの利用方法
by智啓 出川
 
2015年度GPGPU実践基礎工学　第12回　GPUによる画像処理
by智啓 出川
 
2015年度GPGPU実践基礎工学　第5回　ハードウェアによるCPUの高速化技術
by智啓 出川
 
2015年度GPGPU実践プログラミング　第15回　GPU最適化ライブラリ
by智啓 出川
 
2015年度GPGPU実践基礎工学　第8回　並列計算の概念 （プロセスとスレッド）
by智啓 出川
 
2015年度GPGPU実践プログラミング　第3回　GPGPUプログラミング環境
by智啓 出川
 
2015年度GPGPU実践基礎工学　第11回　GPUでの並列 プログラミング（ベクトル和）
by智啓 出川
 
2015年度GPGPU実践基礎工学　第9回　GPUのアーキテクチャ
by智啓 出川
 

Similar to 2015年度GPGPU実践プログラミング　第8回　総和計算（高度な最適化）

PDF
2015年度先端GPGPUシミュレーション工学特論　第7回　総和計算（Atomic演算）
by智啓 出川
 
PDF
CMSI計算科学技術特論B(14) OpenACC・CUDAによるGPUコンピューティング
byComputational Materials Science Initiative
 
PDF
動的計画法の並列化
byProktmr
 
PPTX
GPUによる多倍長整数乗算の高速化手法の提案
byKoji Kitano
 
PDF
GPU-FPGA 協調計算を記述するためのプログラミング環境に関する研究（HPC169 No.10）
byRyuuta Tsunashima
 
PDF
GPGPU Education at Nagaoka University of Technology: A Trial Run
by智啓 出川
 
PDF
2012-03-08 MSS研究会
byKimikazu Kato
 
PDF
20130126 sc12-reading
byToshiya Komoda
 
PDF
CUDA1日(?)体験会
byRinKuriyama
 
KEY
NVIDIA Japan Seminar 2012
byTakuro Iizuka
 
PDF
More modern gpu
byPreferred Networks
 
PDF
CUDA1日(?)体験会 (再アップロード)
byRinKuriyama
 
PPTX
GPUによる多倍長整数乗算の高速化手法の提案とその評価
byKoji Kitano
 
PDF
Cuda
byShumpei Hozumi
 
PDF
1072: アプリケーション開発を加速するCUDAライブラリ
byNVIDIA Japan
 
PDF
第11回 配信講義　計算科学技術特論B（2022）
byRCCSRENKEI
 
PDF
Hello, DirectCompute
bydasyprocta
 
PDF
技術系大学におけるGPU教育の一試行
by智啓 出川
 
PDF
GPGPU Seminar (GPU Accelerated Libraries, 2 of 3, cuSPARSE)
by智啓 出川
 
PDF
200625material naruse
byRCCSRENKEI
 
2015年度先端GPGPUシミュレーション工学特論　第7回　総和計算（Atomic演算）
by智啓 出川
 
CMSI計算科学技術特論B(14) OpenACC・CUDAによるGPUコンピューティング
byComputational Materials Science Initiative
 
動的計画法の並列化
byProktmr
 
GPUによる多倍長整数乗算の高速化手法の提案
byKoji Kitano
 
GPU-FPGA 協調計算を記述するためのプログラミング環境に関する研究（HPC169 No.10）
byRyuuta Tsunashima
 
GPGPU Education at Nagaoka University of Technology: A Trial Run
by智啓 出川
 
2012-03-08 MSS研究会
byKimikazu Kato
 
20130126 sc12-reading
byToshiya Komoda
 
CUDA1日(?)体験会
byRinKuriyama
 
NVIDIA Japan Seminar 2012
byTakuro Iizuka
 
More modern gpu
byPreferred Networks
 
CUDA1日(?)体験会 (再アップロード)
byRinKuriyama
 
GPUによる多倍長整数乗算の高速化手法の提案とその評価
byKoji Kitano
 
Cuda
byShumpei Hozumi
 
1072: アプリケーション開発を加速するCUDAライブラリ
byNVIDIA Japan
 
第11回 配信講義　計算科学技術特論B（2022）
byRCCSRENKEI
 
Hello, DirectCompute
bydasyprocta
 
技術系大学におけるGPU教育の一試行
by智啓 出川
 
GPGPU Seminar (GPU Accelerated Libraries, 2 of 3, cuSPARSE)
by智啓 出川
 
200625material naruse
byRCCSRENKEI
 

More from 智啓 出川

PDF
Fortranが拓く世界、VSCodeが架ける橋
by智啓 出川
 
PDF
Very helpful python code to find coefficients of the finite difference method
by智啓 出川
 
PDF
Why do we confuse String and Array of Characters in Fortran?
by智啓 出川
 
PDF
Pythonによる累乗近似
by智啓 出川
 
PDF
数値計算結果のPythonによる後処理について（1次元データのピーク値およびその位置の推定）
by智啓 出川
 
PDF
オブジェクト指向Fortranが拓く（はずだった）新しい世界
by智啓 出川
 
PPTX
Schematic diagrams of GPUs' architecture and Time evolution of theoretical FL...
by智啓 出川
 
PDF
GPGPU Seminar (GPU Accelerated Libraries, 1 of 3, cuBLAS)
by智啓 出川
 
PDF
Cuda fortranの利便性を高めるfortran言語の機能
by智啓 出川
 
PDF
PGI CUDA FortranとGPU最適化ライブラリの一連携法
by智啓 出川
 
PPTX
教育機関でのJetsonの活用の可能性
by智啓 出川
 
PDF
GPGPU Seminar (GPGPU and CUDA Fortran)
by智啓 出川
 
PDF
GPGPU Seminar (Accelerataion of Lattice Boltzmann Method using CUDA Fortran)
by智啓 出川
 
PDF
GPGPU Seminar (PyCUDA)
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第15回　CPUとGPUの協調
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第14回　複数GPUの利用
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第13回　数値流体力学への応用 （高度な最適化）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第11回　数値流体力学への応用 （支配方程式，CPUプログラム）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第10回　Poisson方程式の求解 （線形連立一次方程式）
by智啓 出川
 
PDF
2015年度先端GPGPUシミュレーション工学特論　第8回　偏微分方程式の差分計算 （拡散方程式）
by智啓 出川
 
Fortranが拓く世界、VSCodeが架ける橋
by智啓 出川
 
Very helpful python code to find coefficients of the finite difference method
by智啓 出川
 
Why do we confuse String and Array of Characters in Fortran?
by智啓 出川
 
Pythonによる累乗近似
by智啓 出川
 
数値計算結果のPythonによる後処理について（1次元データのピーク値およびその位置の推定）
by智啓 出川
 
オブジェクト指向Fortranが拓く（はずだった）新しい世界
by智啓 出川
 
Schematic diagrams of GPUs' architecture and Time evolution of theoretical FL...
by智啓 出川
 
GPGPU Seminar (GPU Accelerated Libraries, 1 of 3, cuBLAS)
by智啓 出川
 
Cuda fortranの利便性を高めるfortran言語の機能
by智啓 出川
 
PGI CUDA FortranとGPU最適化ライブラリの一連携法
by智啓 出川
 
教育機関でのJetsonの活用の可能性
by智啓 出川
 
GPGPU Seminar (GPGPU and CUDA Fortran)
by智啓 出川
 
GPGPU Seminar (Accelerataion of Lattice Boltzmann Method using CUDA Fortran)
by智啓 出川
 
GPGPU Seminar (PyCUDA)
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第15回　CPUとGPUの協調
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第14回　複数GPUの利用
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第13回　数値流体力学への応用 （高度な最適化）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第11回　数値流体力学への応用 （支配方程式，CPUプログラム）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第10回　Poisson方程式の求解 （線形連立一次方程式）
by智啓 出川
 
2015年度先端GPGPUシミュレーション工学特論　第8回　偏微分方程式の差分計算 （拡散方程式）
by智啓 出川
 

2015年度GPGPU実践プログラミング　第8回　総和計算（高度な最適化）