長岡技術科学大学
2015年度GPGPU実践プログラミング(全15回,学部4年対象講義)
第15回GPU最適化ライブラリ
2015年度GPGPU実践プログラミング
・第1回 GPGPUの歴史と応用例
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59179080
・第2回 GPUのアーキテクチャとプログラム構造
http://www.slideshare.net/ssuserf87701/2015gpgpu2-59179215
・第3回 GPGPUプログラミング環境
http://www.slideshare.net/ssuserf87701/2015gpgpu3-59179255
・第3回補足 GROUSEの利用方法
http://www.slideshare.net/ssuserf87701/2015gpgpu3-59183677
・第4回 GPUでの並列プログラミング(ベクトル和,移動平均,差分法)
http://www.slideshare.net/ssuserf87701/2015gpgpu4-59179449
・第5回 GPUのメモリ階層
http://www.slideshare.net/ssuserf87701/2015gpgpu5-59179536
・第6回 パフォーマンス解析ツール
http://www.slideshare.net/ssuserf87701/2015gpgpu6-59179577
・第7回 総和計算
http://www.slideshare.net/ssuserf87701/2015gpgpu7-59179639
・第8回 総和計算(高度な最適化)
http://www.slideshare.net/ssuserf87701/2015gpgpu8-59179686
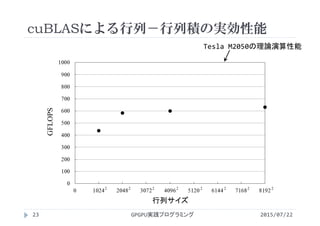
・第9回 行列計算(行列-行列積)
http://www.slideshare.net/ssuserf87701/2015gpgpu9-59179722
・第10回 行列計算(行列-行列積の高度な最適化)
http://www.slideshare.net/ssuserf87701/2015gpgpu10-59179759
・第11回 画像処理
http://www.slideshare.net/ssuserf87701/2015gpgpu11-59179789
・第12回 偏微分方程式の差分計算
http://www.slideshare.net/ssuserf87701/2015gpgpu12-59179972
・第13回 多粒子の運動
http://www.slideshare.net/ssuserf87701/2015gpgpu13-59180018
・第14回 N体問題
http://www.slideshare.net/ssuserf87701/2015gpgpu14-59180054
・第15回 GPU最適化ライブラリ
http://www.slideshare.net/ssuserf87701/2015gpgpu15-59180086
2015年度先端GPGPUシミュレーション工学特論
・第1回 先端シミュレーションおよび産業界におけるGPUの役割
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180313
2015年度GPGPU実践基礎工学
・第1回 学際的分野における先端シミュレーション技術の歴史
http://www.slideshare.net/ssuserf87701/2015gpgpu1
講義には長岡技術科学大学のGPGPUシステム(GROUSE)を利用しています。
開発環境
CPU Intel Xeon X5670 × 32
GPU NVIDIA Tesla M2050(Fermi世代) × 64
CUDA 4.0(諸般の事情によりバージョンアップされていません)
PGI Fortran 11.3







![cuBLAS
2015/07/22GPGPU実践プログラミング8
計算内容に対応した関数を呼ぶ事で計算を実行
cublas<>axpy() ベクトル和
cublas<>gemv() 行列‐ベクトル積
cublas<>gemm() 行列‐行列積
コンパイルの際はオプションとして –lcublas を追加
y[] = x[] + y[]
y[] = OP(A[][])x[] + y[]
C[][] = OP(A[][])OP(B[][]) + C[][]](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-8-320.jpg)
![#include<stdio.h>
#include<math.h>
#include<cublas_v2.h>
#define M 256
#define N 256
int main(){
int i,j;
float A[M*N], B[N], C[M];
float *dev_A, *dev_B, *dev_C;
float alpha, beta;
for(j=0;j<N;j++){
for(i=0;i<N;i++){
A[i+M*j] = ((float) i)/256.0;
}
}
for(i=0;i<M;i++){
C[i] = 0.0f;
}
for(i=0;i<N;i++){
B[i] = 1.0f;
}
cudaMalloc
((void**)&dev_A, N*N*sizeof(float));
cudaMalloc
((void**)&dev_B, N*sizeof(float));
cudaMalloc
((void**)&dev_C, M*sizeof(float));
alpha = 1.0f;
beta = 0.0f;
cuBLASによる行列-ベクトル積
GPGPU実践プログラミング9 2015/07/22
cublas_gemv.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-9-320.jpg)
![cublasHandle_t handle;
cublasCreate(&handle);
cublasSetMatrix
(M, N, sizeof(float), A, M, dev_A, M);
cublasSetVector
(N, sizeof(float), B, 1, dev_B, 1);
cublasSetVector
(M, sizeof(float), C, 1, dev_C, 1);
cublasSgemv
(handle, CUBLAS_OP_N, M, N, &alpha,
dev_A, M, dev_B, 1, &beta, dev_A, 1);
cublasGetVector
(M, sizeof(float), dev_C, 1, C, 1);
for(i=0;i<M;i++){
printf("C[%3d] = %f ¥n",j, C[j]);
}
cudaFree(dev_A);
cudaFree(dev_B);
cudaFree(dev_C);
cublasDestroy(handle);
return 0;
}
cuBLASによる行列-ベクトル積
GPGPU実践プログラミング10 2015/07/22
cublas_gemv.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-10-320.jpg)


![cuBLASによる行列-ベクトル積
2015/07/22GPGPU実践プログラミング13
演算を行う関数の呼び出し
cublasSgemv(handle, CUBLAS_OP_N, M, N, &alpha,
dev_A, M, dev_B, 1, &beta, dev_C, 1);
CUBLAS_OP_N 行列Bに対する操作
cublasOperation_t型
CUBLAS_OP_N OP(B)=B 処理しない
CUBLAS_OP_T OP(B)=BT 転置
CUBLAS_OP_C OP(B)=BH 共役転置
C[M] = OP(A[M][N])B[N] + C[M]
アクセスの
ストライド](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-13-320.jpg)

![cuBLASを使う際の注意点
2015/07/22GPGPU実践プログラミング15
行列を表現するときのメモリ配置
A[i][j]
2次元配列でもメモリ上は1次元に配置
i方向が先かj方向が先か
C言語はj方向優先
Fortranはi方向優先](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-15-320.jpg)
![cuBLASを使う際の注意点
2015/07/22GPGPU実践プログラミング16
C言語におけるA[i][j]のメモリ上の配置
0/256,0/256,0/256・・・1/256,1/256,1/256・・・2/256,2/256,2/256 ・・・
FortranにおけるA(i,j)のメモリ上の配置 ←BLAS
0/256,1/256,2/256・・・0/256,1/256,2/256・・・0/256,1/256,2/256・・・
256/2256/2256/2
256/1256/1256/1
256/0256/0256/0
j
i](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-16-320.jpg)
![cuBLASによる行列-行列積
2015/07/22GPGPU実践プログラミング17
cublasSgemm(cublasHandle_t handle,
char trans_a, char trans_b,
int m, int n, int k,
float alpha, const float *A, int lda,
const float *B, int ldb,
float beta, float *C, int ldc);
trans_a,trans_b
CUBLAS_OP_N, CUBLAS_OP_T, CUBLAS_OP_C
lda, ldb, ldc A,B,Cを格納する配列の行数
C[m][n] = OP(A[m][k])OP(B[k][n]) + C[m][n]](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-17-320.jpg)
![cuBLASによる行列-行列積
2015/07/22GPGPU実践プログラミング18
m,n,kとlda,ldb,ldcの数値による挙動の変化
cublasSgemm(handle,CUBLAS_OP_N, CUBLAS_OP_N,
4, 4, 4, 0.0, A,4, B,4, 0.0, C,4);
配列Aの行方向(第1次元)要素数4,行数4,行列の形状A[4][4]
配列Bの行方向(第1次元)要素数4,行数4,行列の形状B[4][4]
配列Cの行方向(第1次元)要素数4,行数4,行列の形状C[4][4]
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
bbbb
bbbb
bbbb
bbbb
aaaa
aaaa
aaaa
aaaa
cccc
cccc
cccc
cccc](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-18-320.jpg)
![cuBLASによる行列-行列積
2015/07/22GPGPU実践プログラミング19
m,n,kとlda,ldb,ldcの数値による挙動の変化
cublasSgemm(handle,CUBLAS_OP_N, CUBLAS_OP_N,
3, 3, 3, 0.0, A,4, B,4, 0.0, C,4);
配列Aの行方向(第1次元)要素数4,行数3,行列の形状A[3][3]
配列Bの行方向(第1次元)要素数4,行数3,行列の形状B[3][3]
配列Cの行方向(第1次元)要素数4,行数3,行列の形状C[3][3]
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
3,32,31,3
3,22,21,2
3,12,11,1
0000
0
0
0
bbbb
bbbb
bbbb
bbbb
aaaa
aaaa
aaaa
aaaa
ccc
ccc
ccc](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-19-320.jpg)
![cuBLASによる行列-行列積
2015/07/22GPGPU実践プログラミング20
m,n,kとlda,ldb,ldcの数値による挙動の変化
cublasSgemm(handle,CUBLAS_OP_N, CUBLAS_OP_N,
2, 2, 3, 0.0, A,4, B,4, 0.0, C,4);
配列Aの行方向(第1次元)要素数4,行数2,行列の形状A[2][3]
配列Bの行方向(第1次元)要素数4,行数3,行列の形状B[3][2]
配列Cの行方向(第1次元)要素数4,行数2,行列の形状C[2][2]
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
4,43,42,41,4
4,33,32,31,3
4,33,22,21,2
4,13,12,11,1
2,21,2
2,11,1
0000
0000
00
00
bbbb
bbbb
bbbb
bbbb
aaaa
aaaa
aaaa
aaaa
cc
cc](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-20-320.jpg)
![#include<stdio.h>
#include<math.h>
#include<cublas_v2.h>
#define N 4096
int main(){
int i,j;
float *A, *B, *C;
float *dev_A, *dev_B, *dev_C;
float alpha, beta;
A=(float *)malloc(N*N*sizeof(float));
B=(float *)malloc(N*N*sizeof(float));
C=(float *)malloc(N*N*sizeof(float));
for(j=0;j<N;j++){
for(i=0;i<N;i++){
A[i+N*j] = (float)i;
B[i+N*j] = (float)j;
C[i+N*j] = 0.0f;
}
}
cudaMalloc((void**)&dev_A,
N*N*sizeof(float));
cudaMalloc((void**)&dev_B,
N*N*sizeof(float));
cudaMalloc((void**)&dev_C,
N*N*sizeof(float));
alpha = 1.0f;
beta = 0.0f;
cuBLASによる行列-行列積
GPGPU実践プログラミング21 2015/07/22
cublas_gemm.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-21-320.jpg)



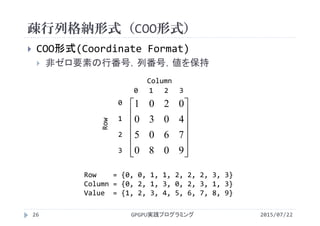
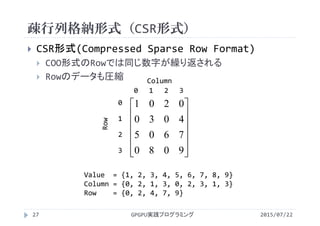
![疎行列格納形式(CSR形式)
2015/07/22GPGPU実践プログラミング28
9080
7605
4030
0201
0 1 2 3
Column
0
1
2
3
Row
Value = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Column = {0, 2, 1, 3, 0, 2, 3, 1, 3}
Row = {0, 2, 4, 7, 9}
Column配列の0,1は0行目のデータ
i行目のデータの個数は Row[i+1]‐Row[i]
forループが簡単に書ける for(j=row[i]; j<row[i+1];j++)](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-28-320.jpg)
![疎行列格納形式(CSR形式)
2015/07/22GPGPU実践プログラミング29
9080
7605
4030
0201
0 1 2 3
Column
0
1
2
3
Row
Value = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Column = {0, 2, 1, 3, 0, 2, 3, 1, 3}
Row = {0, 2, 4, 7, 9}
Column配列の2,3は1行目のデータ
i行目のデータの個数は Row[i+1]‐Row[i]
forループが簡単に書ける for(j=row[i]; j<row[i+1];j++)](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-29-320.jpg)
![疎行列格納形式(CSR形式)
2015/07/22GPGPU実践プログラミング30
9080
7605
4030
0201
0 1 2 3
Column
0
1
2
3
Row
Value = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Column = {0, 2, 1, 3, 0, 2, 3, 1, 3}
Row = {0, 2, 4, 7, 9}
Column配列の4,5,6は2行目のデータ
i行目のデータの個数は Row[i+1]‐Row[i]
forループが簡単に書ける for(j=row[i]; j<row[i+1];j++)](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-30-320.jpg)
![疎行列格納形式(CSR形式)
2015/07/22GPGPU実践プログラミング31
9080
7605
4030
0201
0 1 2 3
Column
0
1
2
3
Row
Value = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Column = {0, 2, 1, 3, 0, 2, 3, 1, 3}
Row = {0, 2, 4, 7, 9}
Column配列の7,8は3行目のデータ
i行目のデータの個数は Row[i+1]‐Row[i]
forループが簡単に書ける for(j=row[i]; j<row[i+1];j++)](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-31-320.jpg)
![cuSPARSEの行列-行列積
2015/07/22GPGPU実践プログラミング32
N×Nの正方行列同士のかけ算
cuBLASの場合
[C] = OP([A])*OP([B]) + [C]
cublasSgemm(handle, OPERATION, OPERATION,
N, N, N, , [A], N, [B], N, , [C], N);
cuSPERSEの場合
[C] = OP([A])*[B] + [C]
cusparseScsrmm(handle, OPERATION, N, N, N, NNZ,
, descr[A], csrVal[A], csrRow[A], csrCol[A],
[B], N, , [C], N);
行列サイズ 行数 行数 行数
行列転置の有無
非ゼロ
要素数行列サイズ
配列Aの詳細情報 配列Aの値 配列Aの行情報 配列Aの列情報](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-32-320.jpg)





![#include<stdio.h>
#include<math.h>
#include<cufft.h>
#define N 256
#define MAX_WAVE 5
int main(){
int i,wavenum;
float real[N],imag[N];
cufftHandle plan;
cufftComplex host[N];
cufftComplex *dev;
cufftComplex re_host[N];
for(i=0;i<N;i++){
real[i] = 0.0;
imag[i] = 0.0;
}
for(wavenum=1;wavenum<=MAX_WAVE;
wavenum++){
for(i=0;i<N;i++){
real[i] +=
cos(2.0*M_PI*(float)i/N
*(float)wavenum);
}
}
for(i=0;i<N;i++){
printf("%f,%f¥n",(float)i,real[i]);
}
for(i=0;i<N;i++){
host[i] = make_cuComplex(
real[i],imag[i]);
}
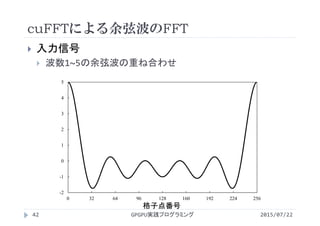
cuFFTによる余弦波のFFT
2015/07/22GPGPU実践プログラミング38
cufft.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-38-320.jpg)
![cudaMalloc((void**)&dev,
N*sizeof(cufftComplex));
cudaMemcpy(dev, host,
N*sizeof(cufftComplex),
cudaMemcpyHostToDevice);
cufftPlan1d(&plan, N, CUFFT_C2C,1);
cufftExecC2C(plan, dev, dev,
CUFFT_FORWARD);
cudaMemcpy(re_host, dev,
N*sizeof(cufftComplex),
cudaMemcpyDeviceToHost);
for(i=0;i<N/2;i++){
printf("dev[%3d] = %f %f ¥n",
i,cuCrealf(re_host[i]),
cuCimagf(re_host[i]));
}
cufftDestroy(plan);
cudaFree(dev);
return 0;
}
cuFFTによる余弦波のFFT
2015/07/22GPGPU実践プログラミング39
cufft.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-39-320.jpg)
![cuFFTによる余弦波のFFT
2015/07/22GPGPU実践プログラミング40
ヘッダファイルのインクルード
#include<cufft.h>
二つの実数(実部と虚部)から複素数を作成
host[i] = make_cuComplex(real[i],imag[i]);
GPU上のメモリ確保
cudaMalloc
1次元FFTのプランを作成
cufftPlan1d(&plan, N, CUFFT_C2C, 1);
N個のデータを使って
1次元FFTを1回行う](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-40-320.jpg)
![cuFFTによる余弦波のFFT
2015/07/22GPGPU実践プログラミング41
複素数から複素数へのFFTを実行
cufftExecC2C(plan, dev, dev,CUFFT_FORWARD);
結果の表示(実部と虚部の取り出し)
cuCrealf(re_host[i]) 複素数の実部を取り出す
cuCimagf(re_host[i]) 複素数の虚部を取り出す
プランの破棄とGPU上のメモリの解放
cufftDestroy(plan);
cudaFree
コンパイルの際はオプションとして –lcufft を追加](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-41-320.jpg)





![#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <curand.h>
#define N 1024
int main(){
int i;
float *value, *value_d;
curandGenerator_t gen;
cudaMalloc((void**)&value_d,
N*sizeof(float));
curandCreateGenerator (&gen,
CURAND_RNG_PSEUDO_DEFAULT);
curandGenerateUniform
(gen, value_d, N);
value
= (float *)malloc(N*sizeof(float));
cudaMemcpy(value, value_d,
N*sizeof(float),
cudaMemcpyDeviceToHost);
for(i=0;i<N;i++){
printf("%d¥n",value[i]);
}
curandDestoryGenerator(gen);
cudaFree(value_d);
free(value);
return 0;
}
cuRANDサンプル
GPGPU実践プログラミング48 2015/07/22
curand.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-48-320.jpg)

![#include<stdio.h>
#include<stdlib.h>
#include<curand_kernel.h>
#define N (1024)
__global__ void random(float *value){
int i
= blockIdx.x*blockDim.x + threadIdx.x;
unsigned int seed;
curandState stat;
seed = 1;
curand_init(seed, i, 0, &stat);
value[i] = curand_uniform(&stat);
}
int main(){
int i;
float *value, *value_d;
cudaMalloc((void**)&value_d,
N*sizeof(float));
random<<<1,1>>>(value_d);
value = (float *)malloc
(N*sizeof(float));
cudaMemcpy(value, value_d,
N*sizeof(float),
cudaMemcpyDeviceToHost);
for(i=0;i<N;i++){
printf("%f ¥n",value[i]);
}
cudaFree(value_d);
free(value);
return 0;
}
cuRANDサンプル
GPGPU実践プログラミング50 2015/07/22
curand_kernel.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-50-320.jpg)

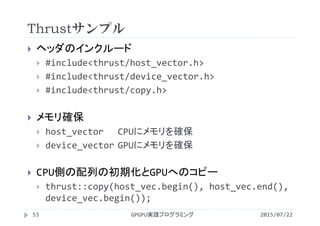
![#include<iostream>
#include<thrust/host_vector.h>
#include<thrust/device_vector.h>
#include<thrust/copy.h>
#include<thrust/sort.h>
int main(void) {
thrust::host_vector < float > host_vec(3);
thrust::device_vector < float > device_vec(3);
host_vec[0] = 1.1; host_vec[1] = 3.3; host_vec[2] = 2.2;
thrust::copy(host_vec.begin(), host_vec.end(), device_vec.begin());
thrust::sort(device_vec.begin(), device_vec.end());
thrust::copy(device_vec.begin(), device_vec.end(), host_vec.begin());
std::cout << host_vec[0] << std::endl;
std::cout << host_vec[1] << std::endl;
std::cout << host_vec[2] << std::endl;
return 0;
}
Thrustサンプル
GPGPU実践プログラミング52 2015/07/22
thrust_sort.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-52-320.jpg)


![#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<curand.h>
#define N 1024
int main(){
int i,inside;
float *x, *y, *x_d, *y_d;
float pi;
curandGenerator_t gen;
cudaMalloc((void**)&x_d, N*sizeof(float));
cudaMalloc((void**)&y_d, N*sizeof(float));
curandCreateGenerator(&gen,
CURAND_RNG_PSEUDO_DEFAULT);
curandGenerateUniform(gen, x_d, N); //x座標
curandGenerateUniform(gen, y_d, N); //y座標
x = (float *)malloc(N*sizeof(float));
y = (float *)malloc(N*sizeof(float));
cudaMemcpy(x, x_d, N*sizeof(float),
cudaMemcpyDeviceToHost);
cudaMemcpy(y, y_d, N*sizeof(float),
cudaMemcpyDeviceToHost);
inside=0;
for(i=0;i<N;i++){
if( (x[i]*x[i] + y[i]*y[i]) <=1.0f )
inside++;
}
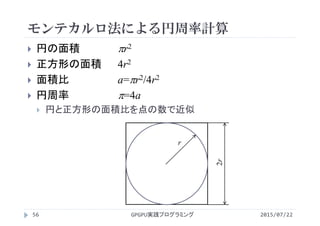
pi = 4.0f*(float)inside/N;
printf("%f¥n",pi);
curandDestroyGenerator(gen);
cudaFree(x_d);
cudaFree(y_d);
free(x);
free(y);
return 0;
}
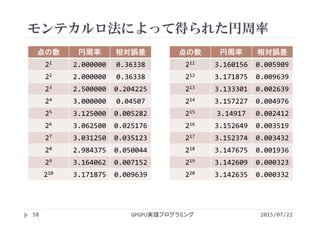
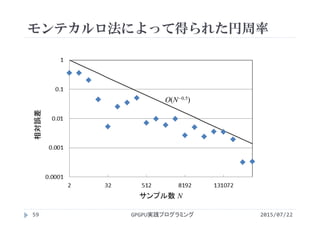
モンテカルロ法による円周率計算
2015/07/22GPGPU実践プログラミング57
montecarlo.cu](https://image.slidesharecdn.com/gpgpuprogramming15-160307053318/85/2015-GPGPU-15-GPU-57-320.jpg)