長岡技術科学大学
2015年度GPGPU実践基礎工学(全15回,学部3年対象講義)
第8回並列計算の概念�(プロセスとスレッド)
2015年度GPGPU実践基礎工学
・第1回 学際的分野における先端シミュレーション技術の歴史
http://www.slideshare.net/ssuserf87701/2015gpgpu1
・第2回 GPGPUの歴史と応用例
http://www.slideshare.net/ssuserf87701/2015gpgpu2
・第3回 GPUクラスタ上でのプログラミング(CUDA)
http://www.slideshare.net/ssuserf87701/2015gpgpu3
・第4回 CPUのアーキテクチャ
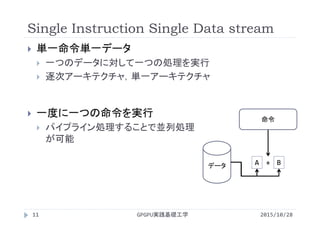
http://www.slideshare.net/ssuserf87701/2015gpgpu4
・第5回 ハードウェアによるCPUの高速化技術
http://www.slideshare.net/ssuserf87701/2015gpgpu5
・第6回 ソフトウェアによるCPUの高速化技術
http://www.slideshare.net/ssuserf87701/2015gpgpu6
・第7回 シングルコアとマルチコア
http://www.slideshare.net/ssuserf87701/2015gpgpu7
・第8回 並列計算の概念(プロセスとスレッド)
http://www.slideshare.net/ssuserf87701/2015gpgpu8
・第9回 GPUのアーキテクチャ
http://www.slideshare.net/ssuserf87701/2015gpgpu9
・第9回補足 GROUSEの利用方法
http://www.slideshare.net/ssuserf87701/2015gpgpu9-59160061
・第10回 GPGPUのプログラム構造
http://www.slideshare.net/ssuserf87701/2015gpgpu10
・第11回 GPUでの並列プログラミング(ベクトル和)
http://www.slideshare.net/ssuserf87701/2015gpgpu11
・第12回 GPUによる画像処理
http://w ww.slideshare.net/ssuserf87701/2015gpgpu12
・第13回GPUのメモリ階層
http://www.slideshare.net/ssuserf87701/2015gpgpu13
・第14回 GPGPU組込開発環境
http://www.slideshare.net/ssuserf87701/2015gpgpu14
・第15回 GPGPUの開発環境(OpenCL)
http://www.slideshare.net/ssuserf87701/2015gpgpu15
2015年度GPGPU実践プログラミング
・第1回 GPGPUの歴史と応用例
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59179080
2015年度先端GPGPUシミュレーション工学特論
・第1回 先端シミュレーションおよび産業界におけるGPUの役割
http://www.slideshare.net/ssuserf87701/2015gpgpu1-59180313
講義には長岡技術科学大学のGPGPUシステム(GROUSE)を利用しています。
開発環境
CPU Intel Xeon X5670 × 32
GPU NVIDIA Tesla M2050(Fermi世代) × 64
CUDA 4.0(諸般の事情によりバージョンアップされていません)
PGI Fortran 11.3











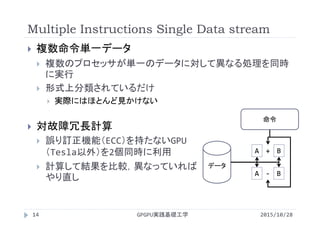

























![OpenMPによる並列化
GPGPU実践基礎工学42
処理を並列実行したい箇所に指示句(ディレクティブ)を
挿入
for文の並列化
ディレクティブを一行追加(#pragma omp ~)
#pragma omp parallel for
for(int i=0; i<N; i++)
C[i] = A[i] + B[i]
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-42-320.jpg)
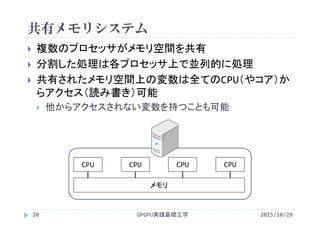
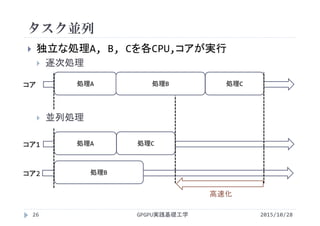
![ベクトル和C=A+Bの計算
配列要素に対して計算順序の依存性がなく,最も単純に
並列化可能
・・・
・・・
・・・c[i]
a[i]
b[i]
+ + + + + +
GPGPU実践基礎工学43 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-43-320.jpg)
![逐次(並列化前)プログラム
GPGPU実践基礎工学44
#include<stdio.h>
#define N (1024*1024)
int main(){
float a[N],b[N],c[N];
int i;
for(i=0; i<N; i++){
a[i] = 1.0;
b[i] = 2.0;
c[i] = 0.0;
}
for(i=0; i<N; i++)
c[i] = a[i] + b[i];
for(i=0; i<N; i++)
printf("%f+%f=%f¥n",
a[i],b[i],c[i]);
return 0;
}
vectoradd.c
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-44-320.jpg)
![逐次(並列化前)プログラム
GPGPU実践基礎工学45
#include<stdio.h>
#include<stdlib.h>
#define N (1024*1024)
#define Nbytes (N*sizeof(float))
int main(){
float *a,*b,*c;
int i;
a = (float *)malloc(Nbytes);
b = (float *)malloc(Nbytes);
c = (float *)malloc(Nbytes);
for(i=0; i<N; i++){
a[i] = 1.0;
b[i] = 2.0;
c[i] = 0.0;
}
for(i=0; i<N; i++)
c[i] = a[i] + b[i];
for(i=0; i<N; i++)
printf("%f+%f=%f¥n",
a[i],b[i],c[i]);
free(a);
free(b);
free(c);
return 0;
}
vectoradd_malloc.c
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-45-320.jpg)

![並列化プログラム(スレッド並列)
GPGPU実践基礎工学47
#include<stdio.h>
#include<stdlib.h>
#define N (1024*1024)
#define Nbytes (N*sizeof(float))
#include<omp.h>
int main(){
float *a,*b,*c;
int i;
a = (float *)malloc(Nbytes);
b = (float *)malloc(Nbytes);
c = (float *)malloc(Nbytes);
//複数スレッドで処理する領域を指定
//この指定だけだと全スレッドが同じ処理を行う
#pragma omp parallel
{
#pragma omp for//for文を分担して実行
for(i=0; i<N; i++){
a[i] = 1.0;
b[i] = 2.0;
c[i] = 0.0;
}
#pragma omp for//for文を分担して実行
for(i=0; i<N; i++)
c[i] = a[i] + b[i];
}
for(i=0; i<N; i++)
printf("%f+%f=%f¥n",
a[i],b[i],c[i]);
free(a);
free(b);
free(c);
return 0;
}
vectoradd.cpp
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-47-320.jpg)
![処理の並列化
データ並列
forループをスレッドの数だけ分割
分割されたforループを各スレッドが実行
実行時間は1/スレッド数になると期待
for(i=0; i<N/2‐1; i++)
c[i] = a[i] + b[i];
for(i=N/2; i<N; i++)
c[i] = a[i] + b[i];
スレッド0
スレッド1
c[i]
a[i]
b[i]
+ + + +
スレッド0 スレッド1
GPGPU実践基礎工学48 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-48-320.jpg)


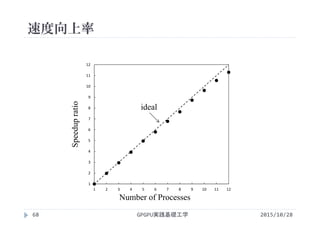
![速度向上率と並列化効率の例
並列度N 計算時間
T(N)[ms]
速度向上率S
=T(1)/T(N)
並列化効率E
=S/N
1 8.00 8.00/8.00 = 1.00 1.00/1 = 1.00
2 4.21 8.00/4.21 = 1.90 1.90/2 = 0.95
3 2.86 8.00/2.86 = 2.78 2.78/3 = 0.93
4 2.16 8.00/2.16 = 3.70 3.70/4 = 0.93
5 1.74 8.00/1.74 = 4.60 4.60/5 = 0.92
6 1.45 8.00/1.45 = 5.52 5.52/6 = 0.92
7 1.25 8.00/1.25 = 6.40 6.40/7 = 0.91
8 1.10 8.00/1.10 = 7.27 7.27/8 = 0.91
9 0.98 8.00/0.98 = 8.16 8.16/9 = 0.91
10 0.88 8.00/0.88 = 9.09 9.09/10 = 0.91
GPGPU実践基礎工学51 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-51-320.jpg)
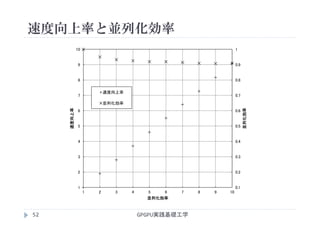

![計算時間の変化
0
1
2
3
4
5
6
1 2 3 4 5 6 7 8 9 10 11 12
Processingtime[ms]
Number of Threads
54 GPGPU実践基礎工学 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-54-320.jpg)






![ベクトル和C=A+Bの計算
配列要素に対して計算順序の依存性がなく,最も単純に
並列化可能
GPGPU実践基礎工学61
・・・
・・・
・・・c[i]
a[i]
b[i]
+ + + + + +
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-61-320.jpg)
![逐次(並列化前)プログラム
GPGPU実践基礎工学62
#include<stdio.h>
#include<stdlib.h>
#define N (1024*1024)
#define Nbytes (N*sizeof(float))
int main(){
float *a,*b,*c;
int i;
a = (float *)malloc(Nbytes);
b = (float *)malloc(Nbytes);
c = (float *)malloc(Nbytes);
for(i=0; i<N; i++){
a[i] = 1.0;
b[i] = 2.0;
c[i] = 0.0;
}
for(i=0; i<N; i++)
c[i] = a[i] + b[i];
for(i=0; i<N; i++)
printf("%f+%f=%f¥n",
a[i],b[i],c[i]);
free(a);
free(b);
free(c);
return 0;
}
vectoradd_malloc.c
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-62-320.jpg)
![並列化プログラム(プロセス並列)
GPGPU実践基礎工学63
#include<stdlib.h>
#include<mpi.h>
#define N (1024*1024)
int main(int argc, char* argv[]){
float *a, *b, *c;
int i, nsize, rank, nproc, bytes;
//MPIのライブラリを初期化して実行準備
MPI_Init(&argc, &argv);
//全ノード数を取得
MPI_Comm_size(MPI_COMM_WORLD,
&nproc);
//各ノードに割り振られた固有の番号を取得
MPI_Comm_rank(MPI_COMM_WORLD,
&rank);
//各ノードで処理するデータサイズを設定
nsize = N/nproc;
if(rank==nproc‐1)nsize+=N%nproc;
bytes = sizeof(float)*nsize;
a=(float *)malloc(bytes);//各ノード
b=(float *)malloc(bytes);//でメモリを
c=(float *)malloc(bytes);//確保
//各ノードで配列の初期化と加算を実行
for(i=0;i<nsize;i++){
a[i]=1.0;
b[i]=2.0;
c[i]=0.0;
}
for(int i=0;i<nsize;i++)
c[i] = a[i]+b[i];
//全ノードの同期を取る
MPI_Barrier(MPI_COMM_WORLD);
free(a);
free(b);
free(c);
MPI_Finalize();//MPIのライブラリを終了
return 0;
} vectoradd_mpi.cpp
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-63-320.jpg)

![処理の並列化
データ並列
forループをスレッドの数だけ分割
分割されたforループを各ノードが実行
実行時間は1/スレッド数になると期待
c[i]
a[i]
b[i]
+ + + +
ノード0 ノード1
GPGPU実践基礎工学65
for(i=0; i<N/2‐1; i++)
c[i] = a[i] + b[i];
for(i=0; i<N/2‐1; i++)
c[i] = a[i] + b[i];
ノード0
ノード1
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-65-320.jpg)

![計算時間の変化
Processingtime[ms]
Number of Threads
67 GPGPU実践基礎工学
0
1
2
3
4
5
6
7
8
9
1 2 3 4 5 6 7 8 9 10 11 12
OpenMP
MPI
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-67-320.jpg)










![OpenMPによる総和計算の並列化
計算順序に依存性はないが,出力結果に依存性がある
・・・
sum
a[i]
+ + + + + +
GPGPU実践基礎工学80 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-80-320.jpg)
![逐次(並列化前)プログラム
GPGPU実践基礎工学81
#include<stdio.h>
#include<stdlib.h>
#define N 100
#define Nbytes (N*sizeof(float))
int main(){
float *a,sum=0.0f;
int i;
a = (float *)malloc(Nbytes);
for(i=0; i<N; i++)
a[i] = (float)(i+1);
for(i=0; i<N; i++)
sum += a[i];
printf("%f¥n",sum);
return 0;
}
sum_serial.c
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-81-320.jpg)
![並列化プログラム(スレッド並列)
GPGPU実践基礎工学82
#include<stdio.h>
#include<stdlib.h>
#include<omp.h>
#define N 100
#define Nbytes (N*sizeof(float))
int main(){
float *a, sum=0.0f;
int i;
a = (float *)malloc(Nbytes);
#pragma omp parallel for
for(i=0; i<N; i++)
a[i] = (float)(i+1);
#pragma omp parallel for ¥
num_threads(4) reduction(+:sum)
for(i=0; i<N; i++)
sum += a[i];
printf("%f¥n",sum);
return 0;
}
//num_threads()でスレッド数を設定
//reduction(+:sum)でsumに値の合計を集約
sum.cpp
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-82-320.jpg)
![データ競合
GPGPU実践基礎工学83
reduction()を付けないとどうなるか
実行結果が毎回変わる
データ競合(データレース)が発生
sum
0
スレッド1
スレッド2
1 2 3 4 5 6
a[i]
51 52 53 54 55 56
a[i]
sumの値(0)を参照
2015/10/28
sumの値(0)を参照](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-83-320.jpg)
![データ競合
GPGPU実践基礎工学84
reduction()を付けないとどうなるか
実行結果が毎回変わる
データ競合(データレース)が発生
sum
51
スレッド1
スレッド2
1 2 3 4 5 6
a[i]
51 52 53 54 55 56
a[i]
2015/10/28
0+51をsumに書き込み](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-84-320.jpg)
![データ競合
GPGPU実践基礎工学85
reduction()を付けないとどうなるか
実行結果が毎回変わる
データ競合(データレース)が発生
sum
1
スレッド1
スレッド2
1 2 3 4 5 6
a[i]
51 52 53 54 55 56
a[i]
2015/10/28
0+1をsumに書き込み](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-85-320.jpg)
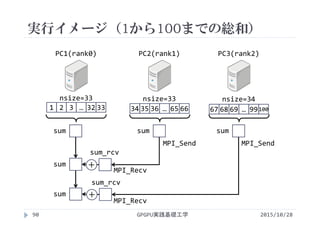
![MPIによる総和計算の並列化
計算順序に依存性はないが,出力結果に依存性がある
OpenMPの時は計算順序が問題
MPIの時はノード間通信が必要
・・・
sum
a[i]
+ + + + + +
GPGPU実践基礎工学86 2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-86-320.jpg)
![並列化プログラム(プロセス並列)
GPGPU実践基礎工学87
#include<stdio.h>
#include<stdlib.h>
#include<mpi.h>
#define ROOT 0 //rank 0のノードは特別扱い
#define N 100
int main(int argc, char* argv[]){
float *a,sum;
int i, nsize, rank, nproc,bytes;
int src, dst,tag;
float sum_rcv;
MPI_Status stat;
//MPIのライブラリを初期化して実行準備
MPI_Init(&argc, &argv);
//全ノード数を取得
MPI_Comm_size(MPI_COMM_WORLD,
&nproc);
//各ノードに割り振られた固有の番号を取得
MPI_Comm_rank(MPI_COMM_WORLD,
&rank);
//各ノードで処理するデータサイズを設定
nsize = N/nproc;
if(rank==nproc‐1) nsize+=N%nproc;
//各ノードでメモリを確保
bytes = sizeof(float)*nsize;
a=(float *)malloc(bytes);
//値の設定
for(i=0;i<nsize;i++)
a[i]=(float)(i+rank*N/nproc+1);
MPI_Barrier(MPI_COMM_WORLD);
sum_mpi.cpp
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-87-320.jpg)
![並列化プログラム(プロセス並列)
GPGPU実践基礎工学88
//各ノードで配列の総和を求める
sum=0.0;
for(i=0;i<nsize;i++)
sum += a[i];
//全ノードの同期を取る
MPI_Barrier(MPI_COMM_WORLD);
//各ノードの総和の値をrank0に送る
if(rank != ROOT){
//rank0以外のノードはrank0に
//sumの値を送信
dst=ROOT;
tag=0;
MPI_Send(&sum, 1, MPI_FLOAT,
dst, tag, MPI_COMM_WORLD);
}else{
//rank0はそれ以外の全ノードから
//送られてくる値を受信し,総和を計算
for(src=ROOT+1; src < nproc;
src++){
tag=0;
MPI_Recv(&sum_rcv, 1,
MPI_FLOAT, src, tag,
MPI_COMM_WORLD, &stat);
sum +=sum_rcv;
}
}
if(rank == ROOT)
printf("%f¥n",sum);
free(a);
MPI_Finalize();//MPIのライブラリを終了
return 0;
}
sum_mpi.cpp
2015/10/28](https://image.slidesharecdn.com/gpgpubasic08-160306181418/85/2015-GPGPU-8-88-320.jpg)