Downloaded 11 times
![ 1つの関数を複数のブロック
関数
により同時に処理可能 ・
◦ 右図のように同一のコードを参 ・
・
照
A[ID]=A[ID]*2+1
スレッドのID
・
◦ どのブロックのどのスレッドな ・
・
のかを表す番号
◦ 異なるスレッドに異なる動作を
させる鍵
7 Next⇒提案手法](https://image.slidesharecdn.com/gpu-121123101621-phpapp02/85/GPU-7-320.jpg)
![ 多倍長整数A×Bの積表
◦ Aは5桁、Bは3桁
◦ BASEは多倍長整数の基数
◦ BASE=10なら10進数
◦ A[0]がAの1の位の数
～～～～～～～～～～～～～～～～～～～
要素の規則性
◦ 2行ごとに添字が1変わる
◦ 桁数を変えても同様
10 Next⇒積表の一般化](https://image.slidesharecdn.com/gpu-121123101621-phpapp02/85/GPU-10-320.jpg)
GPUによる多倍長整数乗算の高速化手法の提案
- 1. 理学部 情報数理科学科 4回生 藤本研究室所属 北野晃司
- 2. 現在主流の整数型 ◦ int(32bit) ◦ long long（64bit） 多倍長整数演算 ◦ より大きいbit数の整数を対象とした演算 ◦ 研究が盛ん GPGPU ◦ GPUによる汎用計算 ◦ 近年注目されつつある 2 Next⇒動機・目的
- 3. 多倍長整数演算は時間がかかる ◦ 特に積、商、平方根の演算 商、平方根 ◦ ニュートン法を用いて高速化可能 高速な乗算が使える場合 GPUを用いて多倍長整数乗算を高速に解く手法を提 案 ※ニュートン法による逆数を求める漸化式⇒Xn+1=2*Xn－a*Xn^2 平方根を求める漸化式⇒Xn+1=(Xn + a/Xn) /2 aは適当な初期 値 3 Next⇒提案内容
- 4. 積表という並列処理に適した データ構造とその処理法の提案 ２つの多倍長整数の和を高速に求める アルゴリズムの提案 時間の都合により割 愛 4 Next⇒発表の流れ
- 5. GPUによる並列処理の概要 提案手法 ◦ 積表 ◦ 積表に対する効率的な処理法の提案 評価実験 まとめと今後の課題 5
- 6. スレッド ― GPUによる並列処理の 最小単位 スレッドブロック ◦ スレッドの集まり スレッ スレッドブロッ ク ド （以下ブロッ ク） 6 Next⇒GPUプログラムの概要
- 7. 1つの関数を複数のブロック 関数 により同時に処理可能 ・ ◦ 右図のように同一のコードを参 ・ ・ 照 A[ID]=A[ID]*2+1 スレッドのID ・ ◦ どのブロックのどのスレッドな ・ ・ のかを表す番号 ◦ 異なるスレッドに異なる動作を させる鍵 7 Next⇒提案手法
- 8. GPUによる並列処理の概要 提案手法 ◦ 積表 ◦ 積表に対する効率的な処理法の提案 評価実験 まとめと今後の課題 8
- 9. 10進数における積 ◦ 右図のような筆算で求めることが可 • 積表能 ◦–桁上げの処理が必要 筆算を元に得られた表 – 桁上げの計算をその値が必要な 桁上げが無ければ列（桁）ごと 列自身に行わせる に並列に計算できるので – 列ごとの総和が他の列の演算と は・・・？？ は独立に行える 9 Next⇒積表の構成
- 10. 多倍長整数A×Bの積表 ◦ Aは5桁、Bは3桁 ◦ BASEは多倍長整数の基数 ◦ BASE=10なら10進数 ◦ A[0]がAの1の位の数 ～～～～～～～～～～～～～～～～～～～ 要素の規則性 ◦ 2行ごとに添字が1変わる ◦ 桁数を変えても同様 10 Next⇒積表の一般化
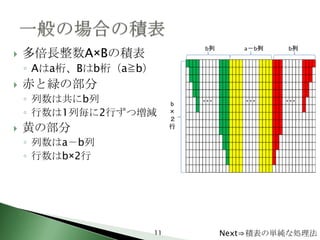
- 11. 多倍長整数A×Bの積表 ◦ Aはa桁、Bはb桁（a≧b） 赤と緑の部分 ◦ 列数は共にb列 ◦ 行数は1列毎に2行ずつ増減 黄の部分 ◦ 列数はa－b列 ◦ 行数はb×2行 11 Next⇒積表の単純な処理法
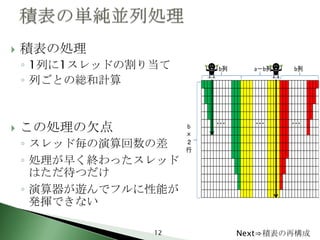
- 12. 積表の処理 ◦ 1列に1スレッドの割り当て ◦ 列ごとの総和計算 この処理の欠点 ◦ スレッド毎の演算回数の差 ◦ 処理が早く終わったスレッド はただ待つだけ ◦ 演算器が遊んでフルに性能が 発揮できない 12 Next⇒積表の再構成
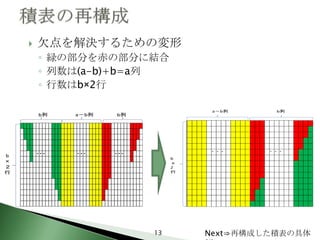
- 13. 欠点を解決するための変形 ◦ 緑の部分を赤の部分に結合 ◦ 列数は(a-b)+b=a列 ◦ 行数はb×2行 13 Next⇒再構成した積表の具体
- 14. 5桁×3桁での例 ◦ 赤と緑、黄、の2種類の長方形 • 列総和に必要な演算回数 – どの列も同じ(2×b 回) • 赤と緑の長方形 – 赤の総和と緑の総和が個別に必要なことに注意 14 Next⇒さらなる工夫
- 15. GPUによる並列処理の概要 提案手法 ◦ 積表 ◦ 積表に対する効率的な処理法の提案 評価実験 まとめと今後の課題 15
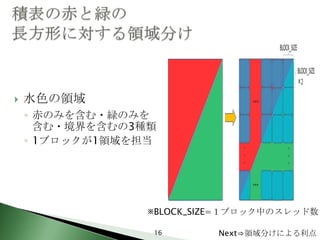
- 16. 水色の領域 ◦ 赤のみを含む・緑のみを 含む・境界を含むの3種類 ◦ 1ブロックが1領域を担当 ※BLOCK_SIZE=１ブロック中のスレッド数 16 Next⇒領域分けによる利点
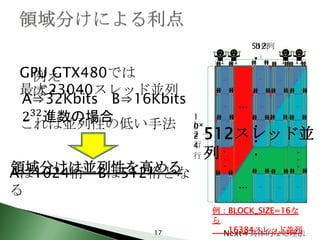
- 17. 512列 b列 ・ GPU GTX480では 例え ・ 最大23040スレッド並列 ば・・・ ・ 1 これは並列性の低い手法 b× 0 ・ 2 2 512スレッド並 ・ 4 行 行 列 ・ 領域分けは並列性を高める Aは1024桁 Bは512桁とな る 例：BLOCK_SIZE=16な ら 17 16384スレッド並列 Next⇒具体的な処理法
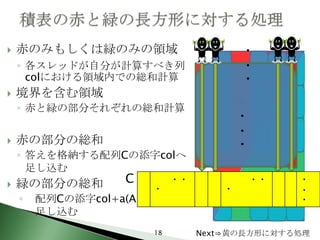
- 18. 赤のみもしくは緑のみの領域 ・ ◦ 各スレッドが自分が計算すべき列 ・ colにおける領域内での総和計算 ・ 境界を含む領域 ◦ 赤と緑の部分それぞれの総和計算 ・ ・ 赤の部分の総和 ・ ◦ 答えを格納する配列Cの添字colへ 足し込む 緑の部分の総和 C ・・ ・・ ・ ・ ・ ・ ◦ 配列Cの添字col+a(Aの桁数)へ ・ 足し込む 18 Next⇒黄の長方形に対する処理
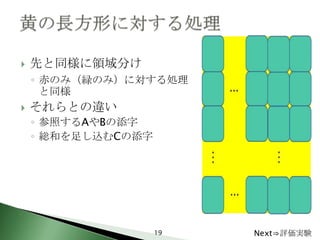
- 19. 先と同様に領域分け ◦ 赤のみ（緑のみ）に対する処理 と同様 それらとの違い ◦ 参照するAやBの添字 ◦ 総和を足し込むCの添字 19 Next⇒評価実験
- 20. GPUによる並列処理の概要 提案手法 ◦ 積表 ◦ 積表に対する効率的な処理法の提案 評価実験 まとめと今後の課題 20
- 21. NTL（A Library for doing Number Theory） ◦ CPUによる多倍長演算ライブラリ ◦ 本実験の比較対象 ◦ 出典：http://www.shoup.net/ntl/ NTLと提案するアルゴリズムの比較 ◦ 6種類のbit数において36通りの組み合わせの 多倍長整数乗算の実行時間 21 Next⇒実験環境
- 22. CPU ◦ 2.93GHz Intel Core i3（1コアのみ使用，SSE命令未使 用） GPU ◦ NVIDIA GeForce GTX480 OS ◦ 64bit Windows7 Professional SP1 コンパイラ ◦ Visual Studio 2008 Professional CUDA ◦ Ver 3.2 ディスプレイドライバ ◦ Ver 285.62 22 Next⇒実験結果
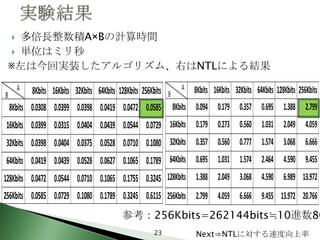
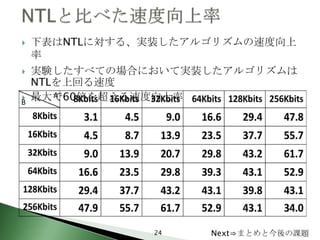
- 23. 多倍長整数積A×Bの計算時間 単位はミリ秒 ※左は今回実装したアルゴリズム、右はNTLによる結果 参考：256Kbits=262144bits≒10進数80 23 Next⇒NTLに対する速度向上率
- 24. 下表はNTLに対する、実装したアルゴリズムの速度向上 率 実験したすべての場合において実装したアルゴリズムは NTLを上回る速度 最大で60倍を超える速度向上率 24 Next⇒まとめと今後の課題
- 25. GPUによる並列処理の概要 提案手法 ◦ 積表 ◦ 積表に対する効率的な処理法の提案 評価実験 まとめと今後の課題 25
- 26. 実装したアルゴリズムは既存の多倍長演算 ライブラリを上回る速度 今回は最大256Kbitsという相当大きい数までを想定 ◦ 実際の問題では数Kbits程度が主流 ◦ 対象を絞ることでさらなる高速化手法が考えられる可能性大 26