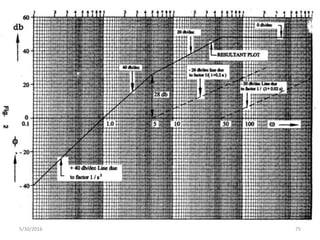
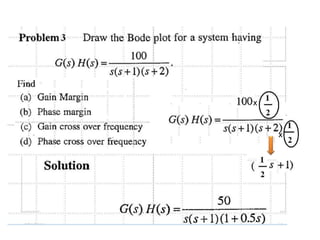
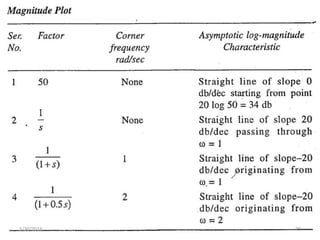
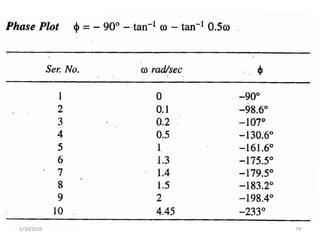
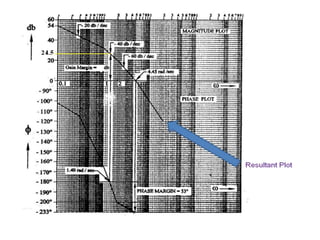
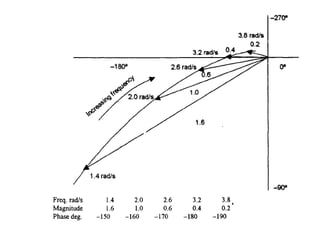
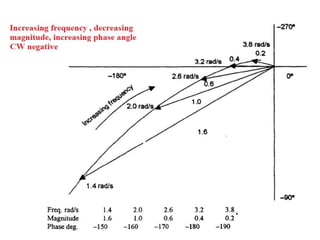
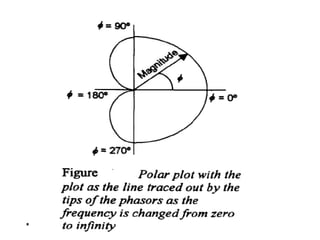
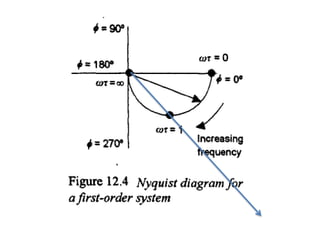
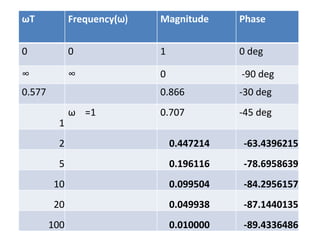
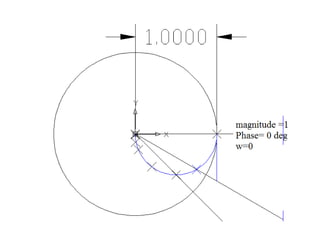
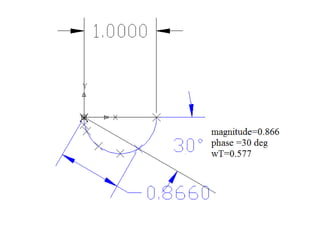
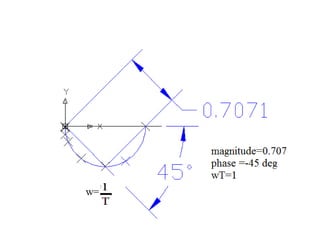
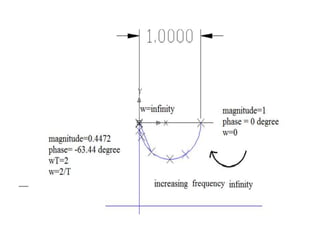
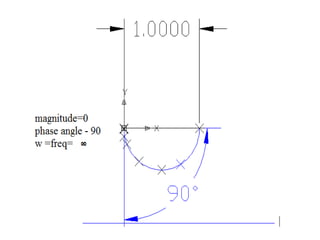
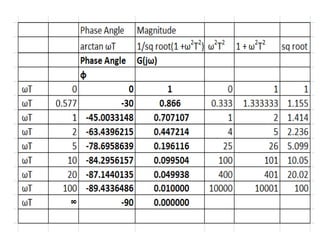
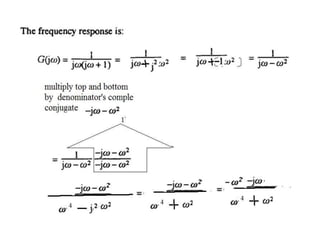
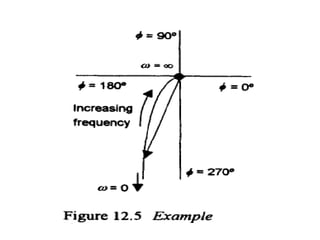
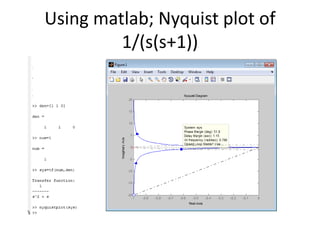
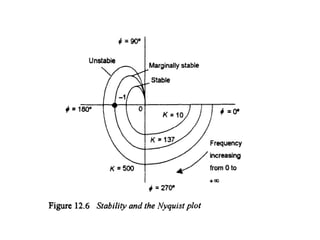
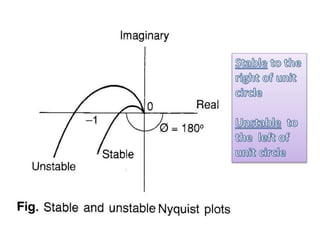
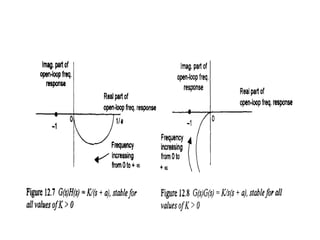
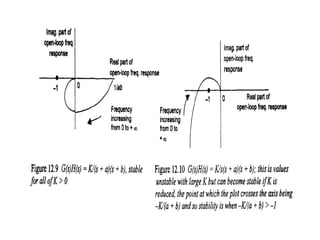
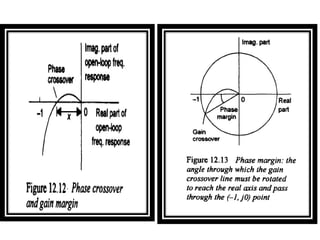
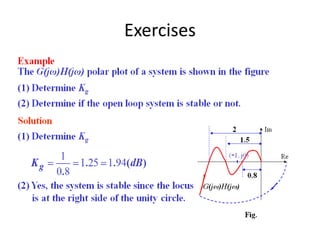
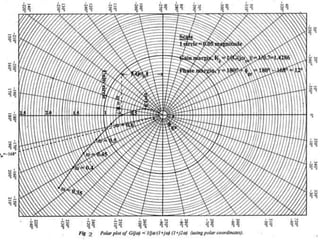
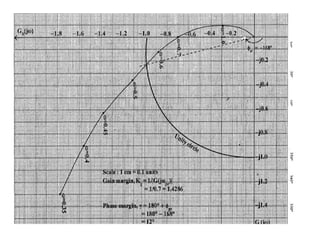
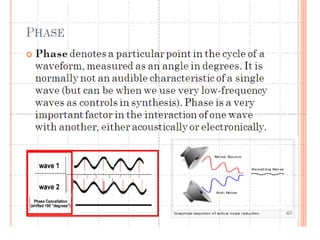
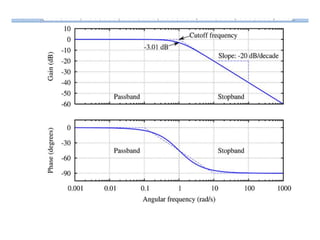
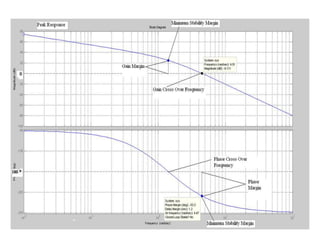
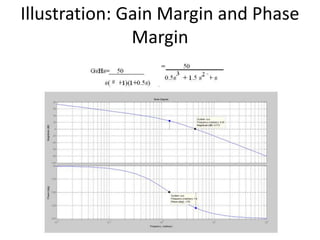
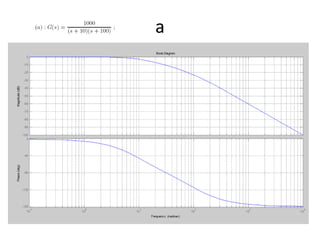
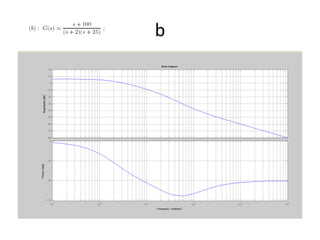
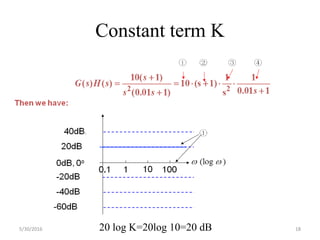
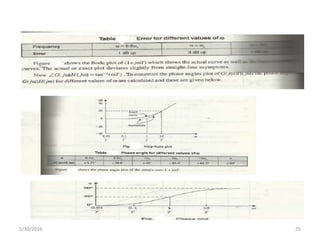
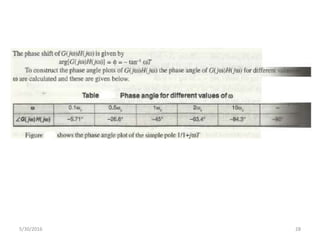
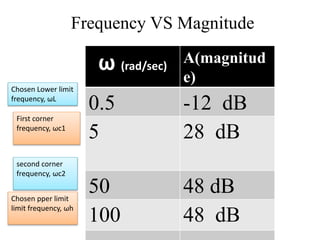
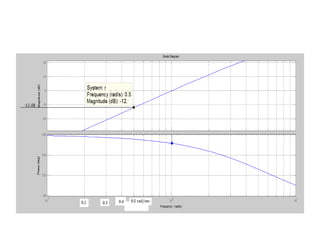
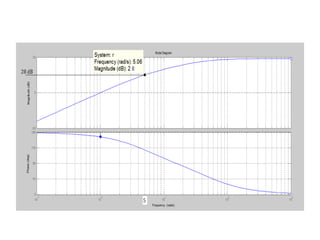
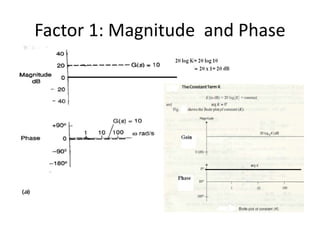
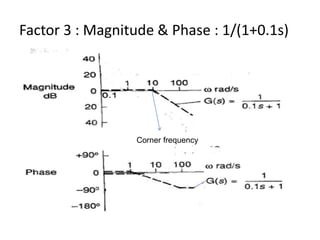
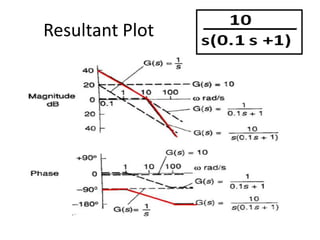
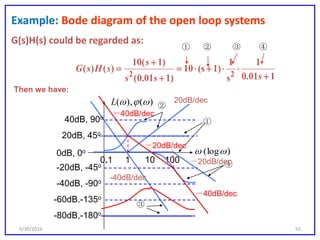
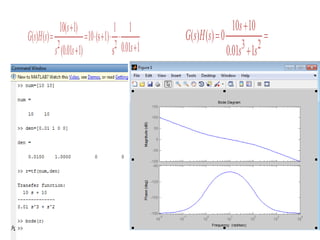
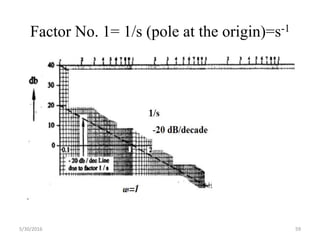
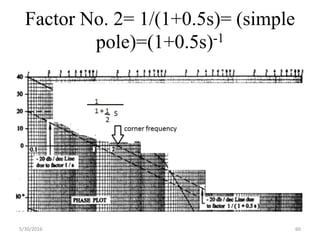
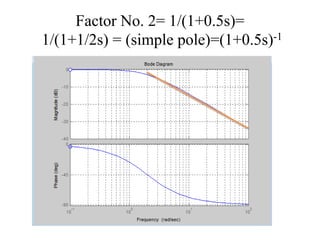
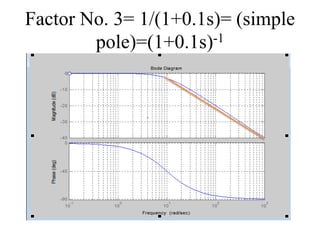
This document discusses frequency response analysis and Nyquist stability criterion. It begins with introductions to frequency, amplitude, phase, and Bode plots. A Bode plot shows the magnitude and phase of a system's frequency response on logarithmic scales. Key points include the gain and phase crossover frequencies. The document then covers Nyquist plots, which show the system's frequency response in the complex plane. The Nyquist stability criterion uses Nyquist plots to determine stability by examining where the plot intersects the real axis. Gain and phase margins are stability metrics calculated from the frequency response. MATLAB is demonstrated for constructing Bode and Nyquist plots. Homework involves populating tables of frequency response data and making plots.

1. Chapter 5
Week 12 -Frequency Response Analysis
Topics:
Control System Engineering
PE-3032
Prof. CHARLTON S. INAO
Defence Engineering College,
Debre Zeit , Ethiopia

2. Introduction to Frequency
Response

3. Terminologies- Frequency , Amplitude ,
Phase
• Frequency, or its inverse, the period- is the
number of occurrences of a repeating event
per unit time. The number of cycles per unit
of time is called the frequency.
The hertz (symbol Hz) is the SI unit of frequency defined as the
number of cycles per second of a periodic phenomenon. One
of its most common uses is the description of the sine wave,
particularly those used in radio and audio applications, such
as the frequency of musical tones. The word "hertz" is named
for Heinrich Rudolf Hertz, who was the first to conclusively
prove the existence of electromagnetic wave.
• Period is the inverse of frequency

5. Bode Plot :Introduction
• The plot of magnitude as well as phase angle
versus frequency may represent a sinusoidal
transfer function.
• Hendrik Wade Bode used the logarithmic
scale extensively for the study of the
magnitude of the transfer function and the
frequency variable. The logarithmic plot is
called Bode Plot.

6. • A Bode plot, named after Hendrik Wade Bode,
is usually a combination of a Bode magnitude
plot and Bode phase plot:
• A Bode magnitude plot is a graph of log
magnitude against log frequency often used in
signal processing to show the transfer
function or frequency response of a linear,
time-invariant system.

7. Phase and Gain Cross Over
Frequency
The gain cross over frequency is the frequency
at which the magnitude of the open loop
transfer function is UNITY.
The phase cross over frequency is the
frequency at which the phase of the open loop
transfer function is 180o.

11. Illustration: Gain Margin and Phase
Margin

12. a

13. b

14. Bode Plot Construction

15. 5/30/2016 15

16. 5/30/2016 16

17. 5/30/2016 17

18. Constant term K
20 log K=20log 10=20 dB5/30/2016 18

19. 5/30/2016 19

20. Zeros and poles at the origin
5/30/2016 20

21. 5/30/2016 21

22. 5/30/2016 22

23. 5/30/2016 23

24. Simple Zero
5/30/2016 24

25. 5/30/2016 25

26. Simple Pole
5/30/2016 26

27. 5/30/2016 27

28. 5/30/2016 28

29. Quadratics/2nd order
5/30/2016 29

30. Bode Plot Example

31. S2/(0.004s2 +0.22 S +1)

34. Frequency VS Magnitude
ω (rad/sec)
A(magnitud
e)
0.5 -12 dB
5 28 dB
50 48 dB
100 48 dB
First corner
frequency, ωc1
second corner
frequency, ωc2
Chosen Lower limit
frequency, ωL
Chosen pper limit
limit frequency, ωh

38. Semilog paper

41. MATLAB

44. Phase Margin
12.6 degrees

46. Draw the asymptote of the Bode plot for the system
having transfer function G(s)=10/s(0.1 s +1)
*****Asymptote Exercise******

47. Magnitude Plot

48. Factor 1: Magnitude and Phase

49. Using MATLAB

50. Factor 2 : Magnitude & Phase(1/s)

51. Factor 3 : Magnitude & Phase : 1/(1+0.1s)
Corner frequency

52. Using MATLAB : 1/(1+0.1s)

53. Resultant Plot

54. MATLAB: Resultant Plot

55. Example: Bode diagram of the open loop systems
G(s)H(s) could be regarded as:
Then we have:
101.0
1
s
1
1)(s10
)101.0(
)1(10
)()(
22 




sss
s
sHsG
① ② ③ ④
0dB, 0o
1001010.1
)(log
)(),( L
③
④
②
①
20dB, 45o
-20dB, -45o
-40dB, -90o
40dB, 90o
-80dB,-180o
-60dB.-135o
-40dB/dec
－20dB/dec
20dB/dec
－40dB/dec
－20dB/dec
－40dB/dec
5/30/2016 55

56. 101.0
1
s
1
1)(s10
)101.0(
)1(10
)()(
22 




sss
s
sHsG 



23
101.0
1010
0)()(
ss
s
sHsG

57. Solved Problems
5/30/2016 57

58. 5/30/2016 58

59. Factor No. 1= 1/s (pole at the origin)=s-1
5/30/2016 59

60. Factor No. 2= 1/(1+0.5s)= (simple
pole)=(1+0.5s)-1
5/30/2016 60

61. Factor No. 2= 1/(1+0.5s)=
1/(1+1/2s) = (simple pole)=(1+0.5s)-1

62. Factor No. 3= 1/(1+0.1s)= (simple
pole)=(1+0.1s)-1
5/30/2016 62

63. Factor No. 3= 1/(1+0.1s)= (simple
pole)=(1+0.1s)-1

64. Factor 4:Constant= K=10
5/30/2016 64
20 log K
20log 10=20 X 1= 20 dB

65. Factor 4 , K=10

66. Phase Angles
5/30/2016 66

67. Computing the phase angle using
MS Excel
5/30/2016 67

68. 5/30/2016 68

69. 5/30/2016 69

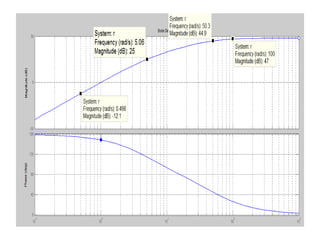
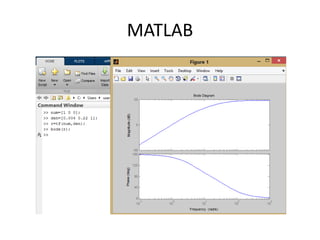
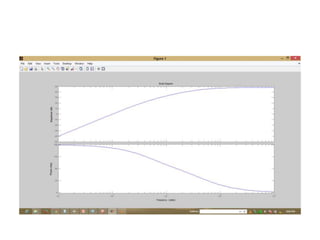
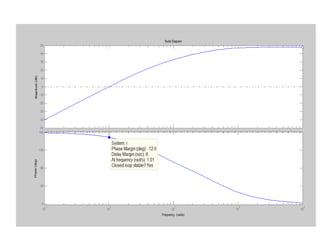
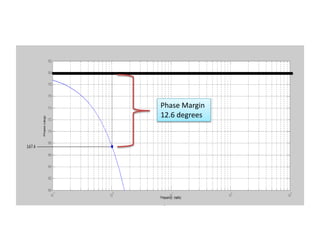
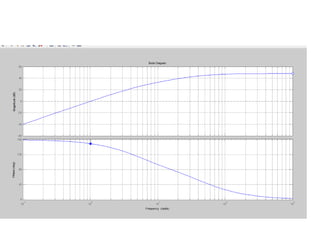
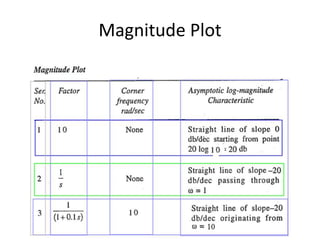
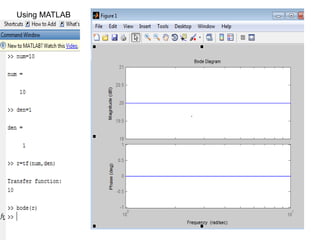
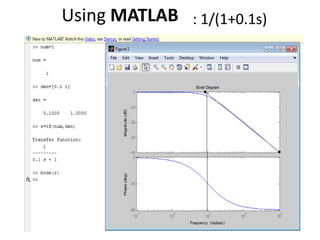
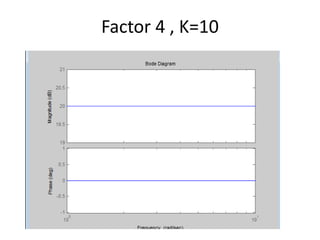
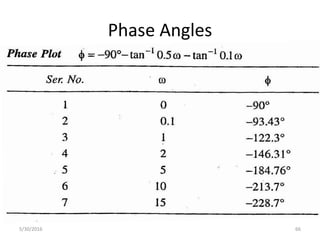
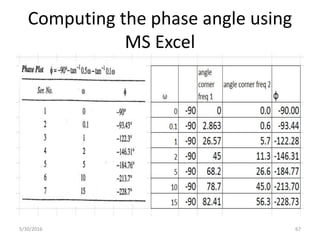
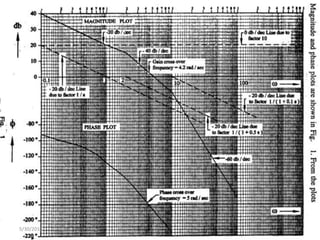
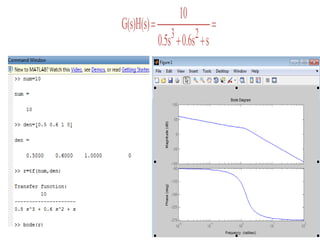
70. Using Matlab



s0.6s0.5s
10
G(s)H(s)
23
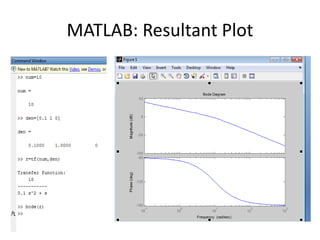
Num=10
Den=[0.5 0.6 1 0 ]
r=tf(num,den)
Bode(r)
commands

71. 


s0.6s0.5s
10
G(s)H(s)
23

72. 5/30/2016 72

73. 5/30/2016 73

74. 5/30/2016 74

75. 5/30/2016 75

76. 5/30/2016 76

77. x
x

78. 5/30/2016 78

79. 5/30/2016 79

81. 5/30/2016 81

82.  (rad/sec)
dB Mag
Phase
(deg)
1 1 1 1 1 1
wlg
This is a sheet of 5 cycle, semi-log paper.
This is the type of paper usually used for
preparing Bode plots.
Semi log paper used in Bode Plots

83. Nyquist Stability
Criterion

84. Week 12 Frequency Response Analysis
Topics:
Control System Engineering
PE-3032
Prof. CHARLTON S. INAO
Defence Engineering College,
Debre Zeit , Ethiopia

85. Instructional Objectives
At the end of this lecture, the students shall be able to:
1. Conduct review of Frequency Response
fundamentals
2. Discuss the parameters in Nyquist Plot construction
3. Understand Nyquist Stability Criterion

86. Nyquist Plot

93. Frequency
(ω)
Magnitude Phase
0 1 0 deg
∞ 0 -90 deg
ω =1 1/√2 -45 deg

96. ωT Frequency(ω) Magnitude Phase
0 0 1 0 deg
∞ ∞ 0 -90 deg
0.577 0.866 -30 deg
1
ω =1 0.707 -45 deg
2 0.447214 -63.4396215
5 0.196116 -78.6958639
10 0.099504 -84.2956157
20 0.049938 -87.1440135
100 0.010000 -89.4336486

106. Using matlab; Nyquist plot of
1/(s(s+1))

107. STABILTY and Nyquist plot

116. Summary
Gain Margin= reciprocal of the magnitude of
the locus of frequency response as it first
touch the real axis, i. e.,at the phase cross
over frequency. Kg=1/G(jw)pc
Phase Margin= the angle through which the gain
cross over line must be rotated to reach the real axis
and pass through the unit circle(gain cross over
frequency)
(-1, j0). γ= 180 +φgc

117. Exercises

120. Homework/Assignment
Populate or make a complete table for phase angle,
frequency and magnitude
Make a clean and neat plot using suitable scale