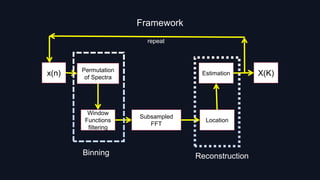
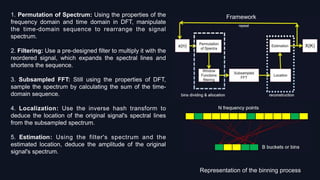
1. The Sparse Fourier Transform (SFT) algorithm takes advantage of the sparsity of signals to efficiently compute their frequency spectra. It does this by mapping frequency points into "bins" and only calculating the non-zero frequency components, reducing computational load. 2. The core ideas of SFT are permuting the signal spectrum, filtering it using a flat-top window function, and taking a subsampled fast Fourier transform (FFT). This converts the signal into a shorter sequence for FFT while maintaining spectral accuracy. 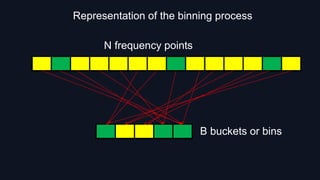3. By adding up frequency points in each "bin" and ignoring empty bins, SFT reconstructs the original spectrum using far fewer computations than a standard discrete Fourier transform, allowing it to handle

1. Simple and Practical
Algorithm for
Sparse Fourier Transform
Haitham Hassanieh MIT | Piotr Indyk MIT | Dina Katabi MIT | Eric Price MIT
Dony Ma

2. WHAT is SFT
SFT is an algorithm that uses the inherent characteristics of a signal to obtain its frequency spectrum.
For a one-dimensional signal, the "inherent characteristics" generally refers to the fact that only a few
frequency components have significant magnitudes within its frequency range, while the magnitudes of
most other frequency components tend to or equal zero.
First and foremost，we should learn about what DFT is :
DFT is a discrete representation of the FT in both the time domain and frequency domain, that means it
transforms a finite-length time-domain discrete sampled sequence into an equally-lengthed frequency-
domain discrete sampled sequence.
Simply put, it can be looked on as a discrete version (i.e. samples) of the DTFT (discrete-time Fourier
transform)
, and 0 ≤ k ≤ N-1
DFT
DTFT

3. WHY we need SFT
Using the traditional Discrete Fourier Transform (DFT) to compute the spectrum of a sparse signal is
a waste of time and space, as most calculations are aimed at frequency components with zero
values.
However, the Sparse Fourier Transform takes advantage of the sparsity of the signal, allowing for the
calculation of only non-zero frequency components, thereby greatly reducing the computational load
and increasing computing speed.
The Sparse Fourier Transform is widely used in areas such as signal processing, image
compression, and machine learning. Compared to the traditional DFT, the SFT can handle much
larger signals and has faster operation speed and lower computational complexity.

4. HOW it works
The core idea of SFT is to use the sparsity of a signal in frequency
domain.
It maps the frequency points into a group of "bins" according to a
certain rule Γ(•) and uses a filter to implement B bins. Because the
frequency domain of the signal is sparse, most numerical points are
likely to exist independently in their respective "bins".
By adding up the frequency points in each "bin", it is possible to
convert an N-point long sequence into a short B-point sequence for
FFT operation.
Based on the calculation results, all "bins" that do not contain
important numerical points are ignored.
Finally, using the corresponding rule Γ(•) for "binning", a
reconstruction algorithm Γ-1(•) is designed to recover the original N-
signal spectrum.
The basic idea of SFT is to minimize the amount of computation
required while ensuring the accuracy of information.
Framework
Representation of the binning process

5. Subsampled
FFT
Estimation
Location
X(K)
Window
Functions
filtering
Permutation
of Spectra
x(n)
repeat
Binning Reconstruction
Framework

6. 1. Permutation of Spectrum: Using the properties of the
frequency domain and time domain in DFT, manipulate
the time-domain sequence to rearrange the signal
spectrum.
2. Filtering: Use a pre-designed filter to multiply it with the
reordered signal, which expands the spectral lines and
shortens the sequence.
3. Subsampled FFT: Still using the properties of DFT,
sample the spectrum by calculating the sum of the time-
domain sequence.
4. Localization: Use the inverse hash transform to
deduce the location of the original signal's spectral lines
from the subsampled spectrum.
5. Estimation: Using the filter's spectrum and the
estimated location, deduce the amplitude of the original
signal's spectrum.
Framework
Representation of the binning process

7. N frequency points
B buckets or bins
Representation of the binning process

8. 1. Choose a random σ, τ ∈ [n] with σ odd.
2. Define y = G · (Pσ,τ x), so yi = Gixσi+τ . Then supp(y) ⊆ supp(G) = [w]
3. Compute ˆzi = ˆyi(n/B) for i ∈ [B]. By Claim 3.7. this is the DFT of zi = ∑j=0
⌈w / B⌉−1 yi+jB .
4. Define the ”hash function” hσ : [n] → [B] by hσ (i) = round(σiB/n)
and the ”offset” oσ : [n] → [−n/(2B), n/(2B)] by oσ (i) = σi− hσ (i)(n/B).
5. Location loops: let J contain the dk coordinates of maximum magnitude in ˆz.
Output I = {i ∈ [n] | hσ (i) ∈ J}, which has size dkn/B.
6. Estimation loops: for i ∈ I, estimate ˆxi as ˆx′i = ˆzhσ (i)ωτ i/ ˆGoσ (i)
Algorithm

9. 1. Permutation of Spectrum:
MIT method of Permutation of Spectra: select a certain probability and permutate datas by the properties of DFT
1. DFT two properties:
Shifting property: if x1 (n) =x(n)WN
bn , X1 (k) = X(k+b) ;
if x2 (n) =x(n-b) , X2 (k) = WN
bkX(k) ;
Scaling property: if x3 (n) =x (σn) , X2 (k ) = X(σ-1k) ;
(σσ-1 ) mod N =1 ,
σ-1 is the number-theoretic inverse of σ
The formula for the transform is (Pσ,τ
x)i = xσi+τ, which means that the i-th
element of the transformed vector is
equal to the element of x that is
located at position σi+τ. In other
words, the elements of x are
rearranged based on the values of σ
and τ.
Define the transform Pσ,τ such that,
given an n-dimensional vector x,
an integer σ that is invertible mod n,
and an integer τ ∈ [n] ,
The associated permutation on a vector
x is given by (Pσ,τ x)i = xσi+τ
(Pσ,τ x)i = xσi+τ
=>
2. The property that the selection of σ mainly follows :
This mainly illustrates the signal can be reconstructed and Pσ,τ
is a permutation of x.
In sum, we denote that p (n) = x(σn+τ) and P (σk) = X(k) WN
-τk

10. 1. Permutation of Spectra
Why permutation ?
Since the high values in the frequency domain are concentrated together, and they need to be
scattered to ensure the sparsity of the frequency domain.
It can be seen that the larger N is , the greater the probability of scattering will be.
From this perspective, σ is related to B, and σ reflects the minimum spacing between adjacent
frequency points, while N/B determines the width of each bucket.
Representation of the binning process

11. 2. Filtering
Why
Filtering?
First, we need to learn about Window functions and Spectral leakage.
We need to cut a long signal into smaller pieces and process on each piece.
As we will see shortly, this can lead to a problem called spectral leakage, which is an issue that
cannot be fully handled. However, its influence can be reduced by window functions.
For example :
x(t) = A1cos(2π.* f1 .*t - φ1) + A2cos(2π.*f2.*t - φ2) + A3cos(2π .*f3.*t - φ3)
==DFT==>
x(t) composed of three cosine waves
In the frequency domain plot without any spectral leakage, and no window function is required.
NOW, LET’S shorten the size of each block and observe what happens.

12. shorten the size of each block
DFT
We haven't changed the signal itself, we've only
shortened the length of each block.
BUT the blocked signal is no longer periodic and
the DFT process treats it as if it were periodic.
Therefore, the frequency components we see in the
first graph have been compressed, and some of
their energy has leaked into adjacent frequencies.
This is spectral leakage.
The same signal exhibits two different
frequency specturms. WHY?
Red one is the original signal
Blue one is the reconstructed signal
(DFT look it on as a periodic signal)
When the signal tries to quickly
adjust to where it thinks it
should be at the start of the
next block, some of the signal's
energy is leaking into higher
frequencies.

13. How do window functions reduce spectral leakage?
The discontinuity of the signal between each block causes spectral leakage.
The discontinuity between blocks is exactly the issue that window functions
should address.
All kinds of Window functions share a common goal that ensure the signal
is zero or approximately zero at the beginning and the end of each block.

14. 2. Filtering
According to the number of bins (B), the 2pi frequency domain is equally divided into B parts, each with a
bandwidth of 2pi/B.
In ideal situations, using a rectangular window filter alone would be sufficient.
However, the ideal rectangular window filter corresponds to sinc sequence with infinitely long “ tails ” in time
domain. But in reality, we can use filters with smoothed transition bands and multiply or convolve them with the
ideal rectangular window to improve its performance.
In this way, we can make the magnitude-frequency characteristic of the resulting filter as close as possible to
that of the ideal rectangular window within a certain sequence length.
The resulting window is named a "flat-top window"， denoted G(k) and g(n) here.
This filter with smoothed transition bands should
be contrained by this Definition2 in their paper:
B ≥1,δ>0,a>0
(1-α)N/(2B) ≤ i ≤ N/(2B)
y (n) =p (n)g (n)
y(n) is obtained by filtering
The constraint condition also limits the
error between the estimated spectrum
G' and the actual spectrum G of the
signal.

15. use a Gaussian window as an example
In time domain, the sinc signal has infinite tails. To address this issue, a Gaussian
window can be applied to smooth out the tails, that means multiplying the sinc signal
and the Gaussian window together in time domain.
It is equivalent to convolving them in frequency domain.
Multiplied by
time domain
smoothed

16. Complete Spectrum of Sinc Signal
Multiplied by Gaussian Window
Frequency Domain
transition bands

17. The combination of spectrum Permutation and Filtering operations is referred to as "Binning".
Binning refers to the transformation of the positions (1~N) of spectral lines in the original signal spectrum
to a new set of positions (1~B) through a series of transformations, where the amplitude at each new
position is obtained as a sum of N/B amplitudes from the original signal spectrum.
It is its sparsity that is highlighted here:
since the amplitudes of most points tend to approach zero, there is a high probability that only one
spectral line will be present in each bin.
Binning
Representation of the binning process
(1~N)
(1~B)

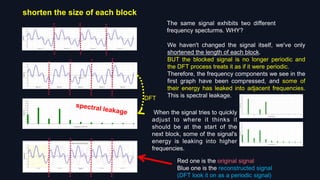
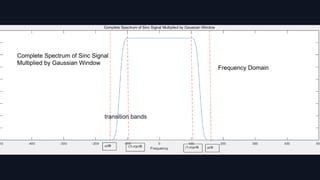
18. 3. Subsampled FFT:
To subsample the frequency domain X(k) to obtain all the maximum
value points with the same interval N/B:
Y(k) =P(k N/B) , k ∈ [0,B -1]
Nevertheless，It is not easy to directly operate in frequency domain.
Instead, we can accomplish this step by time domain aliasing.
Permutation of Spectra:
p (n) = x(σn+τ)
P (σk) = X(k) WN
-τk
As Frequency domain sampling
theorem said: Frequency domain
s am pl i ng c aus es peri odic
replication of the time domain
sequence. When the number of
sampling points in one period in
the frequency domain is greater
than or equal to the number of
points in the time domain
sequence, it will not cause time
domain aliasing. If this condition
is not satisfied, it will cause time
domain aliasing.
Firstly, we have a time-domain sequence p[n] with length j. We perform DTFT on it,
obtaining its frequency spectrum P(ejω).
Then, we sample the frequency spectrum with a period of B points to obtain Y[k] =
P(ejωk). Then, we perform IDFT on Y[k], obtaining y[n].
The formula represents the relationship between y[n] and p[n] after time
domain aliasing.

19. 3. Subsampled FFT:
To subsample the frequency domain X(k) to obtain all the maximum
value points with the same interval N/B:
Y(k) =P(k N/B) , k ∈ [0,B -1]
Nevertheless，It is not easy to directly operate in frequency domain.
Instead, we can accomplish this step by time domain aliasing.
Therefore, after the time-domain aliasing of the signal, performing an FFT operation
with B points can obtain a frequency domain subsampled sequence that contains all
the maximum value points.
Permutation of Spectra:
p (n) = x(σn+τ)
P (σk) = X(k) WN
-τk

20. The dashed line in the left figure represents the position and amplitude of the original signal, while
the solid line represents the spectrum after convolution with a filter.
The total number of points is N=256 and the number of bins is B=8,
So 32 points are added in each bin. The addition operation in the time domain is equivalent to the
sampling operation in the frequency domain.
The sampling points are 0, 32, 64, 96, 128, 160, 192, and 224.
(0,32,64,96,128,160,192 => 0,1,2,3,4,5,6,7)
The number of samples
has been reduced from
256 to 8
Example

21. 4. Localization:
Core idea:
Use the inverse hash transform to get the location of the original signal's spectral lines from the
subsampled spectrum.
The process of mapping the original signal spectrum from its original position to a new one after
being "binned" is similar to the process of "hash mapping" , because each position corresponds
to an amplitude.
The method of signal reconstruction using this idea is called "hash mapping".
Here, the Hash mapping is define :
hσ (k) = round (σkB / N )
oσ(k) =σk-hσ(k) (N/B)

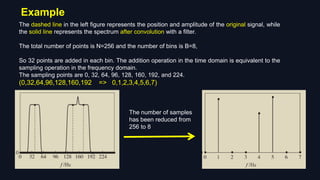
22. 4. Localization:
Firstly, the signal frequency sequence Z(k) obtained after
subsampling the FFT.
Select the coordinates of the top dK maximum values Z(ki) ,
i ∈[0 , dK-1], and put their frequency point k into set J.
Why we select dK coordinates
instead of K coordinates?
After spectrum permutation, filtering,
subsampling, and other operations, additional
frequency components are inevitably
generated. So selecting more coordinates
helps to identify which "bins" contain useful
signals and which "bins" contain useless
signals.
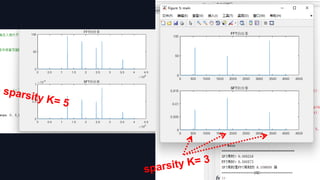
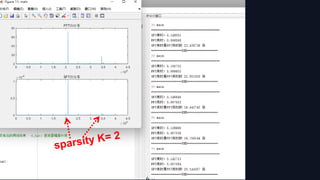
K : sparsity
d : a positive integer
used to determine
the computational
precision
Then obtain the J’s original frequency set through hash
inverse-mapping.
Ir ={ k∈ [0,N -1] | hσ(k) ∈J }

23. 5. Estimation:
The idea behind amplitude estimation :
dividing the value in each bin by the Gain of the filter to obtain an estimated value Xr(k),
Xr(k) means the amplitude corresponding to the frequency value obtained from each bin after inverse
mapping .
In the spectrum, two pieces of information are needed: frequency and amplitude. The previous step of
"locating" solves the former, determining which frequency components are actually being used, while
this step addresses the latter, namely, what is the amplitude of each frequency component.
X(k) = median( { Xr(k) | r ∈ {1,2, … ,L} } )
In each localization cycle, a set Ir is obtained : Ir ={ k∈ [0,N -1] | hσ(k) ∈J }
In L cycles,
for any coordinate k ∈ I = I1 ∪ I2 ........ ∪ IL,
if its frequency is greater than L/2, it is classified into the set I′, and set I′ contains all target frequency
point coordinates.
For each k ∈ I′, the median value of X(k) obtained from L cycles is taken as the final frequency value.

24. Experiment results
The first figure shows that for a large range of signal sizes, sFFT is faster than FFTW and the state-of-
the-art sublinear algorithm.
The second figure shows that sFFT significantly extends the range of applications for which sparse
approximation of DFT is practical, and beats the runtime of FFTW for values of k order of magnitude
larger than those achieved by past work.

25. This figure shows that both sFFT and AAFFT 0.9 are stable under noise but
sFFT has lower errors

29. DFT : O(N*N)
FFT: O( N*log(N) )
SFFT: O( K*log(N)*log(N/K) )
Because the FFT cannot identify the zero elements in a signal sequence, its algorithm treats both zero and non-zero
elements equally, whereas the SFFT can identify these zero elements and only operates on the non-zero elements,
eliminating unnecessary operations and naturally improving the efficiency of the operation compared to the FFT.

30. Spectrum Sensing:
A working receiver that can acquire a bandwidth 6x larger
than the its sampling rate enabling realtime GHz spectrum
sensing using cheap components typically used in WiFi
receivers.
Applications
Magnetic Resonance Imaging (MRI):
Magnetic resonance spectroscopy (MRS)
detects the biochemical content of each voxel in
the brain and can be used to discover disease
biomarkers. Processing MRS data using sparse
FFT enhances image quality, and reduces the
time the patient has to spend in the machine by
3x.

31. Applications
GPS:
We harnessed the sparse FFT to reduce the
time and power it takes a GPS receiver to lock
on its location.
Nuclear Magnetic Resonance (NMR):
NMR is used to discover 3D structure of proteins. We
demonstrated that sparse FFT reduces experiment time
by 16×; enabling high-dimensional NMR, which is needed
for complex proteins
In addition to the above applications, SFT is also widely used in fields such as wireless
communications, optical field photography, spread spectrum capture, radar. At the same time, it
has shown enormous potential for applications in optical coherence tomography (OCT), DNA
sequencing, seismic data analysis, wireless astronomy, and other areas.

32. Promotion of SFT
1. extending the SFT algorithm theory from the Fourier domain to other transform domains
2. extending the SFT algorithm theory to higher dimensions.
3. use different reconstruction methods instead of hash mapping
4. use different filters and window functions

33. 马悦淇
Dony Ma
Electronic and Information Engineering
School of Computer Science and Engineering
Faculty of Innovation Engineering
Macau University of Science and Technology
2009853li011004@student.must.edu.mo
1.https://oi-wiki.org/math/number-theory/basic/
2.https://zh.wikipedia.org/zh-cn/数论
3.《一切皆是映射：代码的本质》Hash算法
4.https://github.com/bernielampe1/sparse_fft
5.Hassanieh H, Indyk P, Katabi D, et al. Simple and practical algorithm for sparse fourier transform[C] ∥Proceedings of
Annual ACM-SIAM Symposium on Discrete Algorithms. [ S. l. ]: ACM, 2012: 1183 1194.
6.http://spiral.net/index.html
7.Hassanieh H, Indyk P, Katabi D, et al. Nearly optimalsparse fourier transform[C] ∥Proceedings of Annual ACM
Symposium on Theory of Computing. [S.l. ]: ACM, 2012:563 577.
8.http://groups.csail.mit.edu/netmit/sFFT/ENC_SFFT.pdf
9.http://groups.csail.mit.edu/netmit/sFFT/Documentation.pdf
10.http://groups.csail.mit.edu/netmit/sFFT/applications.html
11.https://ccrma.stanford.edu/~jos/sasp/Discrete_Time_Fourier_Transform.html
12.Sparse Fast Fourier Transform Code Documentation (SFFT 1.0 and 2.0)
13.陶然, 刘升恒, 张果, 等. 一种利用稀疏傅里叶变换计算外 辐 射 源 雷 达 互 模 糊 函 数 的 方 法