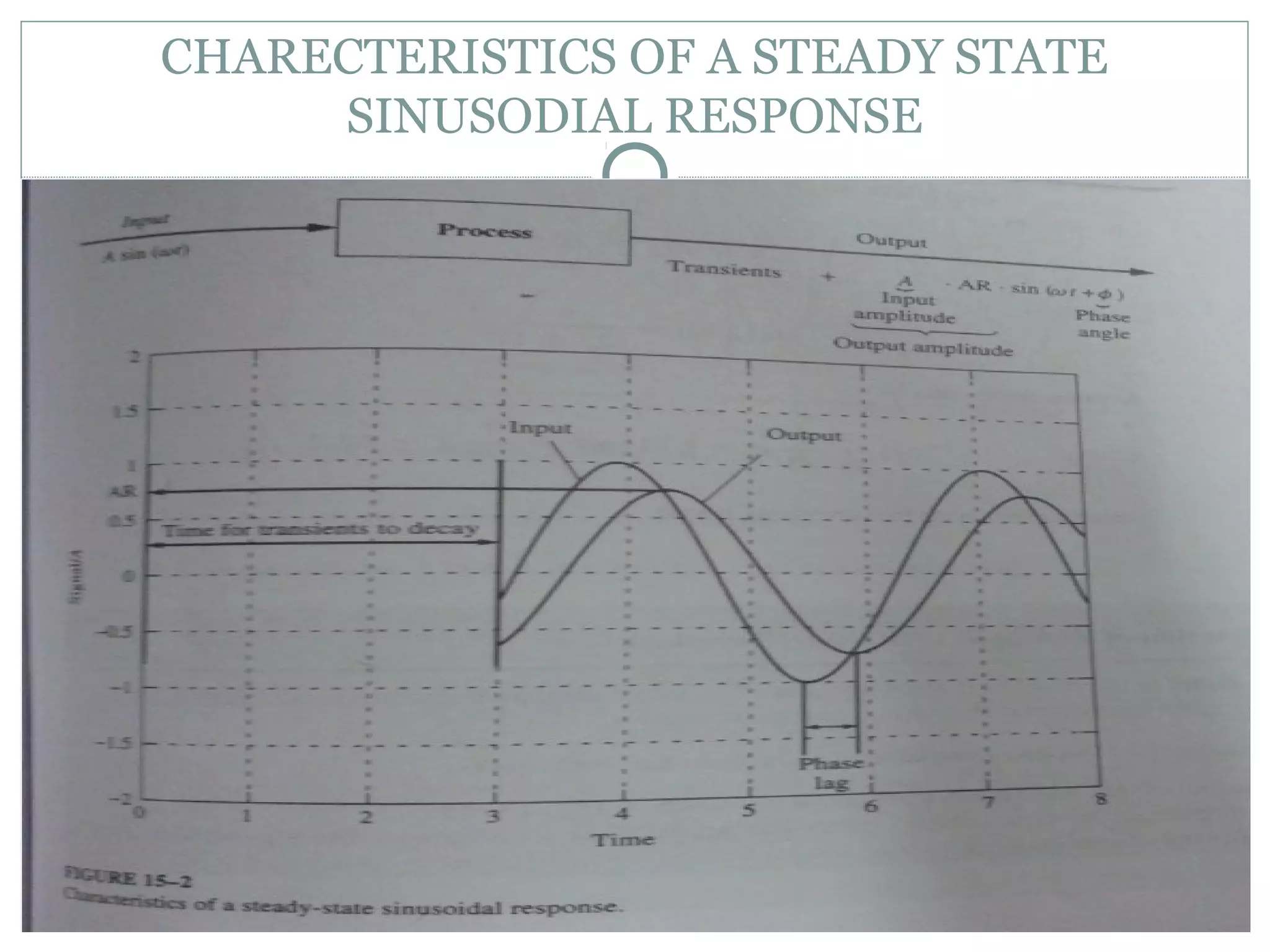
The document discusses frequency response analysis in linear systems using Laplace transforms and graphical techniques like Bode diagrams. It explains key concepts such as amplitude ratio, phase angle, and the characteristics of steady-state sinusoidal responses, highlighting their dependence on frequency. It also covers the construction of Bode diagrams and details the asymptotic behavior of amplitude ratios and phase angles in relation to frequency.

1. PRITESH VASOYA (130420105057)
VISHVARAJ CHAUHAN(130420105058)
VIVEK MISTRY (130420105059)
MILAN HIRAPARA (140423105004)
FREQUENCY RESPONSE
ANALYSIS
Active Learning Assignment, Instrumentation & Process Control
BE SEM V
Chemical Engineering

2. INTRODUCTION
Frequency responses are generally derived by using
the standard Laplace transform of sinusodial forcing
functions.
We shall look at a convenient graphical technique for
obtaining frequency response of linear systems.

3. AMPLITUDE RATIO AND PHASE ANGLE

4. AMPLITUDE RATIO AND PHASE ANGLE

5. AMPLITUDE RATIO AND PHASE ANGLE

6. AMPLITUDE RATIO AND PHASE ANGLE
After sufficient time elapses, the response of a first
order system to a sinusodial input of frequency ω
also a sinusoid of frequency ω.
Amplitude Ratio is defined as output amplitude
upon input amplitude, and is denoted by |G (jω)|.
To obtain AR and phase angle, one merely
substitutes jω instead of s in the transfer function
and then finds the magnitude and angle of the
resulting complex number.

7. CHARECTERISTICS OF A STEADY STATE
SINUSODIAL RESPONSE

8. CHARECTERISTICS OF A STEADY STATE
SINUSODIAL RESPONSE
The output is also a sine wave.
Input frequency=output frequency=ω.
In general, AR < 1, which means output amplitude is
greater than input amplitude.
The output is shifted in time, that is it lags the input
by a phase angle of φ.
Amplitude ratio (AR) and phase angle are both
functions of frequency.

9. BODE DIAGRAMS
There is a convenient graphical representation of AR
and phase lag’s dependence on frequency.
This is called Bode Diagram.
It consists of two graphs: logarithm of AR VS
logarithm of frequency and phase angle versus
logarithm of frequency.
It is plotted on semilog papers.

10. BODE DIAGRAMS

11. BODE DIAGRAMS (FOR FIRST ORDER SYSTEMS)

12. BODE DIAGRAMS (FOR FIRST ORDER SYSTEMS)

13. BODE DIAGRAMS (FOR FIRST ORDER SYSTEMS)
Some asymptotic considerations can simplify the
construction of this plot. As ωτ  0, we can see that
AR1. This is indicated by the low frequency
asymptote.
As ωτ∞ the equation becomes asymptotic to,
log AR = - log(ωτ), which is a line of slope -1, passing
through the point ωτ=1. This is indicated as the high
frequency asymptote.
The frequency ω=1/τ, where the two asymptotes
intersect, is known as the corner frequency.

14. BODE DIAGRAMS (FOR FIRST ORDER SYSTEMS)
In the second part of the Bode Diagram, the phase
curve is given by φ= tan-1
(ωτ)= -tan-1
(ωτ).
φ approaches 0 at low frequencies and -90 at high
frequencies. At corner frequency,
φ= tan-1
(ωτ)= -tan-1
(ωτ)=-tan-1
(1)= -45.
It should be noted that AR is often reported in
decibels. It is defined by, dB= 20 log(AR).

15. THANK YOU.