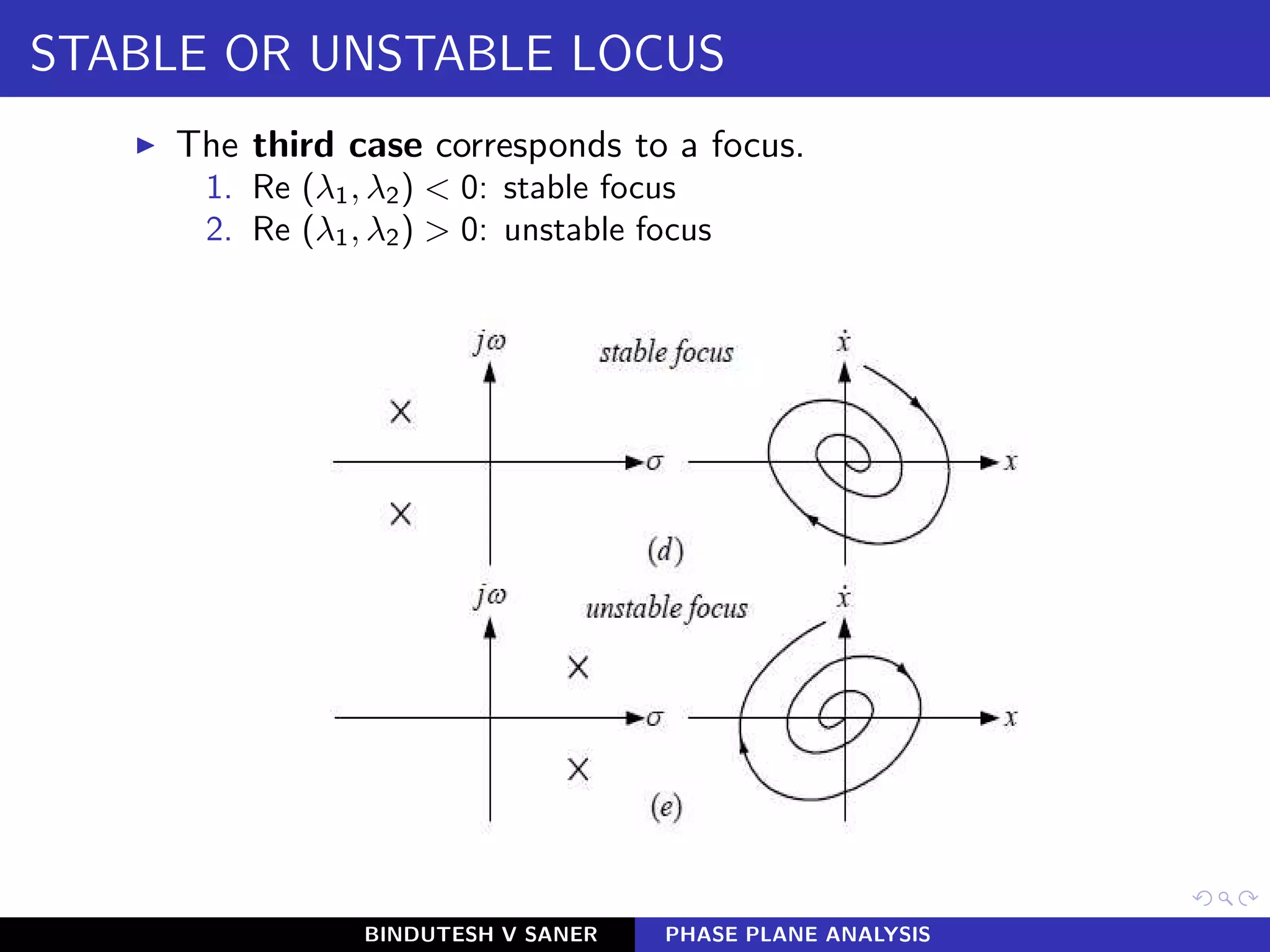
The document discusses phase plane analysis, a graphical method for studying second-order nonlinear systems. It describes phase portraits, singular points, limit cycles, and how to analyze linear and nonlinear systems using the phase plane. Phase plane analysis allows qualitative study of a nonlinear system's behavior from various initial conditions without analytical solutions. While restricted to second-order systems, it provides visualization of trajectories in the phase plane and applies to strong nonlinearities.

1. PHASE PLANE ANALYSIS
BINDUTESH V SANER
May 5, 2015
BINDUTESH V SANER PHASE PLANE ANALYSIS

2. CONTENTS
1. INTRODUCTION
2. BEHAVIOUR OF NON-LINEAR SYSTEM
3. METHOD OF ANALYSIS
4. CLASSIFICATION OF NON-LINEARITIES
5. CONCEPT OF PHASE PLANE ANALYSIS
◮ Phase portraits
◮ Singular point
◮ Phase portraits construction
◮ Phase Plane Analysis of Linear Systems
◮ Phase Plane Analysis of Non-Linear Systems
6. ADVANTAGE and DIS-ADVANTAGE
7. CONCLUSION
8. REFERENCE
BINDUTESH V SANER PHASE PLANE ANALYSIS

3. INTRODUCTION
◮ The most important feature of Nonlinear systems is that
Nonlinear systems do not obey the Principle of
Superposition.
◮ Due to this reason, in contrast to the linear case, the response
of nonlinear systems to a particular test signal is no guide to
their behavior to other inputs.
◮ Phase plane analysis is a graphical method for studying
second-order systems.
◮ The nonlinear system response may be highly sensitive to
input amplitude.
For example, a nonlinear system giving best response for a
certain step input may exhibit highly unsatisfactory behavior
when the input amplitude is changed.
BINDUTESH V SANER PHASE PLANE ANALYSIS

4. BEHAVIOR OF NON LINEAR SYSTEM
◮ The nonlinear systems may exhibit limit cycles which are
self-sustained oscillations of fixed frequency and amplitude.
◮ Once the system trajectories converge to a limit cycle, it will
continue to remain in the closed trajectory in the state space
identified as limit cycles.
◮ In many systems the limit cycles are undesirable particularly
when the amplitude is not small and result in some unwanted
phenomena.
BINDUTESH V SANER PHASE PLANE ANALYSIS

5. METHOD OF ANALYSIS
◮ Nonlinear systems are difficult to analyze and arriving at
general conclusions are tedious.
◮ However, starting with the classical techniques for the solution
of standard nonlinear differential equations, several techniques
have been evolved which suit different types of analysis.
◮ It should be emphasized that very often the conclusions
arrived at will be useful for the system under specified
conditions and do not always lead to generalizations.
BINDUTESH V SANER PHASE PLANE ANALYSIS

6. TYPES OF METHODS FOR ANALYSIS
1. Linearization Techniques
2. Describing Function Analysis
3. Liapunovs Method for Stability
4. Phase Plane Analysis
BINDUTESH V SANER PHASE PLANE ANALYSIS

7. CLASSIFICATION OF NON-LINEARITIES
1. Inherent Non-linearities:The nonlinearities which are present
in the components used in system due to the inherent
imperfections or properties of the system are known as
inherent nonlinearities. for eg. Satuation in
magnetic,Deadzone, Backlash in gear etc
2. Intentional Non-linearities:In some cases introduction of
nonlinearity may improve the performance of the system,
make the system more economical consuming less space and
more reliable than the linear system designed to achieve the
same objective. Such nonlinearities introduced intentionally to
improve the system performance are known as intentional
nonlinearities.
BINDUTESH V SANER PHASE PLANE ANALYSIS

8. CONCEPT OF PHASE PLANE ANALYSIS
◮ phase portraits:The phase plane method is concerned with
the graphical study of second-order autonomous systems
described by
˙x1 = f1(x1, x2) (1)
˙x2 = f2(x1, x2) (2)
◮ where
x1, x2 : states of the system
f1, f2 nonlinear functions of the states
◮ Geometrically, the state space of this system is a plane having
x1, x2 as coordinates.This plane is called Phase plane.
BINDUTESH V SANER PHASE PLANE ANALYSIS

9. ◮ The solution of (1) with time varies from zero to infinity can
be represented as a curve in the phase plane. Such a curve is
called a Phase plane trajectory.
◮ A family of phase plane trajectories is called a phase portrait
of a system.
◮ consider a example of Phase portrait of a mass-spring
system.
Figure: Mass-spring system and its portrait
BINDUTESH V SANER PHASE PLANE ANALYSIS

10. Contd....
◮ The nature of the system response corresponding to various
initial conditions is directly displayed on the phase plane.
◮ In the above example, we can easily see that the system
trajectories neither converge to the origin nor diverge to
infinity. Indicating the marginal nature of the systems stability.
◮ A major class of second-order systems can be described by
the differential equations of the form
¨x = f (x, ˙x)
◮ In state space form, this dynamics can be represented with
x1 = x and x2 = ˙x asfollows :
˙x1 = x2 (3)
˙x2 = f (x1, x2) (4)
BINDUTESH V SANER PHASE PLANE ANALYSIS

11. SINGULAR POINTS
◮ A singular point is an equilibrium point in the phase plane.
Since an equilibrium point is defined as a point where the
system states can stay forever, this implies that ˙x = 0.
◮ For a linear system, there is usually only one singular point
although in some cases there can be a set of singular points.
BINDUTESH V SANER PHASE PLANE ANALYSIS

12. ◮ The general form of a linear second-order system is
˙x1 = ax1 + bx2 (5)
˙x2 = cx1 + dx2 (6)
◮ After solving the above equation we can have a characteristic
equation which can be further solved to have the roots λ1, λ2
can be explicitly represented as
λ1 =
−a +
√
a24b
2
(7)
λ2 =
−a −
√
a2 − 4b
2
(8)
BINDUTESH V SANER PHASE PLANE ANALYSIS

13. ◮ For linear systems there is only one singular point namely the
origin.
However, the trajectories in the vicinity of this singularity
point can display quite different characteristics, depending on
the values of a and b.
The following cases may occur:
1. λ1, λ2 are both real and have the same sign(+ or -).
2. λ1, λ2 are both real and have opposite sign.
3. λ2 are complex conjugates with non-zero real parts.
4. λ1, λ2 are complex conjugates with real parts equal to 0.
◮ Lets briefly discuss above cases.
BINDUTESH V SANER PHASE PLANE ANALYSIS

14. STABLE AND UNSTABLE NODE
◮ The first case corresponds to a node. A node can be stable
or unstable:
1. λ1, λ2 < 0: singularity point is called stable node.
2. λ1, λ2 > 0: singularity point is called unstable node.
BINDUTESH V SANER PHASE PLANE ANALYSIS

15. SADDLE POINT
◮ The second case (λ1 < 0 < λ2 ) corresponds to a saddle
point. Because of the unstable pole λ2, almost all of the
system trajectories diverge to infinity.
Figure:
BINDUTESH V SANER PHASE PLANE ANALYSIS

16. STABLE OR UNSTABLE LOCUS
◮ The third case corresponds to a focus.
1. Re (λ1, λ2) < 0: stable focus
2. Re (λ1, λ2) > 0: unstable focus
BINDUTESH V SANER PHASE PLANE ANALYSIS

17. CENTRE POINT
◮ The last case corresponds to a certain point. All trajectories
are ellipses and the singularity point is the centre of these
ellipses.
Figure:
◮ NOTE: That the stability characteristics of linear systems are
uniquely determined by the nature of their singularity points.
This, however, is not true for nonlinear systems.
BINDUTESH V SANER PHASE PLANE ANALYSIS

18. PHASE PLANE ANALYSIS OF NON-LINEAR SYSTEM
◮ phase plane analysis of nonlinear system,has two important
points as follow:
1. Phase plane analysis of nonlinear systems is related to that of
liner systems, because the local behavior of nonlinear systems
can be approximated by the behavior of a linear system.
2. Nonlinear systems can display much more complicated patterns
in the phase plane, such as multiple equilibrium points and
limit cycles.
◮ LOCAL BEHAVIOUR OF NON-LINEAR SYSTEM:If the
singular point of interest is not at the origin, by defining the
difference between the original state and the singular point as
a new set of state variables, we can shift the singular point
to the origin.
◮ As a result, the local behavior of the nonlinear system can be
approximated by the patterns shown for linear system.
BINDUTESH V SANER PHASE PLANE ANALYSIS

19. LIMIT CYCLE
◮ In the phase plane, a limit cycle is defied as an isolated
closed curve. The trajectory has to be both closed,
indicating the periodic nature of the motion, and isolated,
indicating the limiting nature of the cycle (with near by
trajectories converging or diverging from it).
◮ Depending on the motion patterns of the trajectories in the
vicinity of the limit cycle, we can distinguish three kinds of
limit cycles.
1. Stable Limit Cycles: All trajectories in the vicinity of the
limit cycle converge to it as t → ∞ (Fig a).
2. Unstable Limit Cycles: All trajectories in the vicinity of the
limit cycle diverge to it as t → ∞ (Figb)
3. Semi-Stable Limit Cycles: some of the trajectories in the
vicinity of the limit cycle converge to it as t → ∞(Figc)
BINDUTESH V SANER PHASE PLANE ANALYSIS

20. STABLE,UNSTABLE AND SEMI-STABLE LIMIT CYCLE
Figure: Stable, unstable, and semi-stable limit cycles
BINDUTESH V SANER PHASE PLANE ANALYSIS

21. MERITS AND DEMERITS
◮ MERITS:
1. Phase Plane Analysis is on second-order, the solution
trajectories can be represented by carves in plane provides easy
visualization of the system qualitative behavior.
2. Without solving the nonlinear equations analytically, one can
study the behavior of the nonlinear system from various initial
conditions.
3. It is not restricted to small or smooth nonlinearities and applies
equally well to strong and hard nonlinearities.
4. There are lots of practical systems which can be approximated
by second-order systems, and apply phase plane analysis.
◮ DEMERIT:
1. It is restricted to at most second-order and graphical study of
higher-order is computationally and geometrically complex.
BINDUTESH V SANER PHASE PLANE ANALYSIS

22. CONCLUSION
◮ Phase plane analysis is a graphical method used to study
second-order dynamic systems.
◮ A number of useful classical theorems for the prediction of
limit cycles in second-order systems are also presented.
BINDUTESH V SANER PHASE PLANE ANALYSIS

23. REFERENCES
1. Nguyen Tan Tien (2002-03 ) Applied Nonlinear
Control:chapter 2 Phase Plane Analysis
2. K.T. Alligood, T.D. Sauer, J.A. Yorke (1996).Chaos: An
Introduction to Dynamical Systems. Springer.
BINDUTESH V SANER PHASE PLANE ANALYSIS

24. THANK YOU
BINDUTESH V SANER PHASE PLANE ANALYSIS