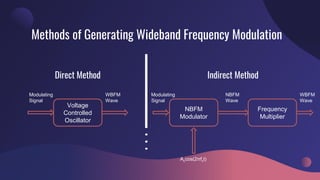
Wideband frequency modulation (WBFM) is a technique where the modulation index is greater than 1, resulting in a wider signal bandwidth. WBFM is used when spectral efficiency is less important and a large spectral spread is desired, such as in entertainment broadcasting, audio communication, and military applications. The mathematical analysis of WBFM shows that its spectrum consists of a carrier signal along with upper and lower sidebands determined by Bessel functions. Its total power is distributed among these components, with greater power in lower order sidebands. WBFM provides better signal quality than narrowband FM but uses more spectrum.

1. WIDEBAND
FREQUENCY MODULATION
Presented By :
Group 9
Ayan Das ▪ Arnab Paul ▪ Arnab Chatterjee ▪ Arijit Dhali
11500320072 ▪ 11500320075 ▪ 11500320076 ▪ 11500320078

2. TABLE OF CONTENTS
WBFM Overview
01
Mathematical Analysis
02
Power and Bandwidth
03
Conclusion and Refernces
04
Frequency Modulation
05

3. In this article, we are going to address applications
and techniques for WBFM with modulation indexes
much larger than 1, going up to 100 and beyond. In
such applications spectral efficiency is less important
and sometimes large spectral spread is actually
desired. The purpose of this article is to present
some major applications in the commercial and
defence markets. Within this framework, the
common techniques of generating WBFM are
presented.
Abstract

4. What is Frequency Modulation?
Frequency modulation (FM) is the encoding of information in
a carrier wave by varying the instantaneous frequency of
the modulating wave. The technology is used
in telecommunications, radio broadcasting, signal processing,
and computing.
There are 2 types of Frequency Modulation:
• Narrow Band Frequency Modulation
• Wide Band Frequency Modulation

5. From the expression of Frequency Modulation we
can narrate,
S(t) = Accos(wct + βsin(wmt))
where, Ac = Carrier Amplitude
β = Modulation Index
However when β>1, then FM is said to be Wide
Band FM (WBFM)
When Wideband Frequency
Modulation occurs?

6. Direct Method
Methods of Generating Wideband Frequency Modulation
Indirect Method
Voltage
Controlled
Oscillator
NBFM
Modulator
Frequency
Multiplier
Modulating
Signal
Modulating
Signal
WBFM
Wave
WBFM
Wave
NBFM
Wave
Accos(2πfct)

7. Bessel Function:
Wideband Frequency Modulation using Bessel Function
Jn(x) =
𝟏
𝟐𝝅
‫׬‬
−𝝅
𝝅
𝒆𝒋(𝒙 𝐬𝐢𝐧 𝜽−𝒏𝜽)
𝒅𝜽
Properties of Bessel Function:
• Jn(x) ↓ when n ↑
∴ J0(x) > J1(x) > J2(x)…
• J-n(x) = (-1)nJn(x)
∴ J-n(x) = Jn(x), when n is even
J-n(x) = -Jn(x), when n is odd
• ‫׬‬
𝒏=−∞
∞
𝑱𝒏
𝟐
𝒙 = 𝟏
• Jn(x) always result in real quantity

8. Plot of Bessel Function

9. Mathematical analysis
General Expression of WBFM:
SFM (t) = AC cos [2π𝑓
𝑐 + β sin(2π 𝑓
𝑚𝑡)] = 𝐴𝐶 cos θ . Thus,
cos 𝜃 = Re e𝑗𝜃
Since, 𝑒𝑗θ
= cos θ + j sin θ
Therefore, 𝑆𝐹𝑀 𝑡 = 𝐴𝐶 𝑅𝑒 𝑒𝑗 2𝜋𝑓𝑐𝑡+𝛽 sin 2π𝑓𝑚𝑡
= 𝐴𝐶 𝑅𝑒 𝑒𝑗 2𝜋𝑓𝑐𝑡
+ 𝑒𝑗(𝛽 sin 2π𝑓𝑚𝑡)
. . . . . . .(1)
In eq (1) , let 𝑓 𝑡 = 𝑒𝑗β sin 2π𝑓𝑚𝑡
is a periodic function with
𝑇 =
1
𝑓𝑚
We know exponential Fourier series,
𝑓 𝑡 = σ𝑛=−∞
∞
𝐶𝑛 𝑒𝑗𝑛𝜔0𝑡
,where 𝜔0 =
2𝜋
𝑇
= 2𝜋𝑓
𝑚
and 𝐶𝑛 =
1
𝑇
‫׬‬−𝑇/2
𝑇/2
𝑓 𝑡 𝑒−𝑗𝑛𝜔0𝑡
𝑑𝑡
𝑒𝑗β sin 2π𝑓𝑚𝑡
= σ𝑛=−∞
∞
𝐶𝑛 𝑒𝑗𝑛2π𝑓𝑚𝑡
. . . . . .(2)
Cn = fm‫׬‬−1/𝑓𝑚
1/𝑓𝑚
𝑒𝑗𝛽𝑠𝑖𝑛2𝜋𝑓𝑚𝑡
.𝑒−𝑗𝑛2𝜋𝑓𝑚𝑡
.dt
= fm‫׬‬−1/𝑓𝑚
1/𝑓𝑚
𝑒𝑗(𝛽𝑠𝑖𝑛2𝜋𝑓𝑚𝑡−𝑛2𝜋𝑓𝑚𝑡)
We Know that,
Jn(x) = -1/2𝜋 ‫׬‬−𝜋
𝜋
𝑒𝑗(𝑥𝑠𝑖𝑛𝜃−𝑛𝜃)
.d𝜃
Assume 2𝜋fmt = 𝜃
or, d𝜃 = 2𝜋fmdt
or, dt = d𝜃/2𝜋𝑓m

10. t = -1/2fm
𝜃 = 2𝜋𝑓𝑚 . −(
1
2𝑓𝑚
) = -𝜋
t = 1/2fm
𝜃 = 2𝜋𝑓𝑚 . (
1
2𝑓𝑚
) = 𝜋
Cn = fm‫׬‬−𝜋
𝜋
𝑒𝑗(𝛽𝑠𝑖𝑛𝜃−𝑛𝜃)
.d𝜃/2fm (fm gets cancelled out)
= 1/2𝜋 ‫׬‬−𝜋
𝜋
𝑒𝑗(𝛽𝑠𝑖𝑛𝜃−𝑛𝜃)
.d𝜃 = Jn(𝛽)
Substituting Cn in equation (2)
𝑒𝑗𝛽𝑠𝑖𝑛2𝜋𝑓𝑚𝑡
= σ𝑛=−∞
∞
Jn(𝛽). 𝑒𝑗𝑛2𝜋𝑓𝑚𝑡
Now substituting this expression with the main equation
Sfm(t) = AcRc[𝑒𝑗2𝜋𝑓𝑐𝑡
. σ𝑛=−∞
∞
Jn(𝛽). 𝑒𝑗𝑛2𝜋𝑓𝑚𝑡
]
= AcRcσ𝑛=−∞
∞
Jn(𝛽). cos2𝜋(fc+nfm)t
SWBFM (t) = Ac σ𝒏=−∞
∞
Jn(𝜷). cos2𝝅(fc+nfm)t (for 𝜷 >1)

11. Power of Wideband Frequency Modulation
We know total power is the sum of carrier power and side
bands power,
P(t) = PC + PUSB1 + PLSB1 + PUSB2 + PLSB2 + . . . . . .
=
𝐴𝑐
2𝐽0
2(𝛽)
2𝑅
+
𝐴𝑐
2𝐽1
2(𝛽)
2𝑅
+
𝐴𝑐
2𝐽−1
2 (𝛽)
2𝑅
+
𝐴𝑐
2𝐽2
2(𝛽)
2𝑅
+
𝐴𝑐
2𝐽2
2(𝛽)
2𝑅
+ . . . . .
=
𝐴𝑐
2
2𝑅
[ J0
2(β) + J1
2(β) + J-1
2(β) + J2
2(β) + J-2
2(β) + . . . . . .]
P(t) =
𝐴𝑐
2
2𝑅
‫׬‬
𝑛=−∞
∞
𝐽𝑛
2
𝛽
∴ P(t) =
𝑨𝒄
𝟐
𝟐𝑹

12. Spectrum of Wideband Frequency Modulation
We know, SWBFM (t) = Ac σ𝑛=−∞
∞
Jn(𝛽). cos2𝜋(fc+nfm)t
= AcJ0(β)cos(2πfct) + AcJ1(β)cos(2πfct) +
AcJ-1(β)cos(2πfct) + AcJ2(β)cos(2πfct) + AcJ-2(β)cos(2πfct) + . . . . .
= AcJ0(β)cos2π(fct) + AcJ1(β)cos2π(fc+fm)t -
AcJ1(β)cos2π(fc-fm)t + AcJ2(β)cos2π(fc+2fm)t +
AcJ2(β)cos2π(fc-2fm)t + . . . . .
𝐴𝑐 𝐽0(𝛽)
2
𝐴𝑐 𝐽2(𝛽)
2
𝐴𝑐 𝐽2(𝛽)
2
𝐴𝑐 𝐽1(𝛽)
2
𝐴𝑐 𝐽1(𝛽)
2
(fc+fm)(fc+2fm)
(fc-fm)
(fc-2fm)
(fc)
SWBFM
Spectrum of WBFM

13. Practical Bandwidth using Carson’s Rule
∴ For (β+1)th Order, BW = (β+1) x 2fm
= (
∆𝑓
𝑓𝑚
+ 1) x 2fm
BW = 2(∆ f + 2fm)
For 3rd Order: BW = 6fm
For 2nd Order: BW = 4fm
For 1st Order: BW = 2fm
2
3
1
(fc+fm)
(fc+2fm)
(fc-fm)
(fc-2fm)
(fc)

14. Applications
The Wide-Band Frequency Modulation is used in the following fields:
• It is used in the entertainment broadcasting applications such as FM radio, TV etc.
• It is used extensively in audio communication and data transfer.
• It is used in free running Voltage Controlled Oscillator (VCO).
• It is used in commercial and defence markets.

15. Conclusion
When spectrum efficiency is important Narrowband FM (NBFM) is
used but when better signal quality is required Wideband FM
(WBFM) is used at the expense of greater spectrum usage. The
term WBFM is used in applications where the modulation index is
equal to or larger than 1.

16. References
● http://contents.kocw.net/KOCW/document/2011/korea/koyoungchai/lecturenote1
7may12.pdf
● https://www.kratosmed.com/gmcatalog/wideband-frequency-modulation-
applications-and-techniques-for-microwave-products
● https://www.researchgate.net/figure/a-The-mathematical-equation-for-Frequency-
Modulation-and-definition-of-terms_fig9_243778275
● https://www.rcet.org.in/uploads/academics/rohini_27413753398.pdf
● https://slideplayer.com/slide/5668316/

17. THANK
YOU
For your patience towards
our presentation