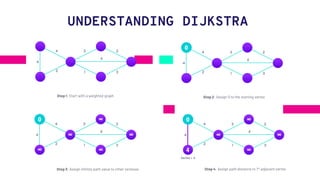
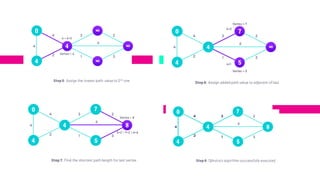
Dijkstra's algorithm allows finding the shortest path between any two vertices in a graph. It works by overestimating the distance of each vertex from the starting point and then visiting neighbors to find shorter paths. The algorithm uses a greedy approach, finding the next best solution at each step. It maintains path distances in an array and maps each vertex to its predecessor in the shortest path. A priority queue is used to efficiently retrieve the closest vertex. The time complexity is O(E Log V) and space is O(V). Applications include social networks, maps, and telephone networks.

1. DIJKSTRA’S ALGORITHM
Represented by Group: 3
• Arijit Dhali
• Ipsita Raha
Department : Electronic & Communication Engineering
Year : 2nd
Session : 2021-22
Data Structure and Algorithm
ES – CSS 301

2. TABLE OF CONTENTS
01
Understanding
Dijkstra
02
Algorithm and
Pseudocode
03
Decoding
04
Complexity

3. What is Dijkstra’s Algorithm ?
Dijkstra's algorithm is an algorithm that
allows us to find the shortest path between
any two vertices of a graph.
DIJKSTRA’S
ALGORITHM

4. Dijkstra's Algorithm works on the basis that any subpath B -> D of the
shortest path A -> D between vertices A and D is also the shortest path
between vertices B and D.
Dijkstra used this property in the opposite direction i.e we
overestimate the distance of each vertex from the starting vertex. Then
we visit each node and its neighbors to find the shortest subpath to
those neighbors.
The algorithm uses a greedy approach in the sense that we find the
next best solution hoping that the end result is the best solution for
the whole problem.
HOW DIJKSTRA’S ALGORITHM
WORK?

5. UNDERSTANDING DIJKSTRA

7. We need to maintain the path distance of every vertex. We can store that in an array of
size v, where v is the number of vertices.
We also want to be able to get the shortest path, not only know the length of the shortest path.
For this, we map each vertex to the vertex that last updated its path length.
Once the algorithm is over, we can backtrack from the destination vertex to the source vertex to
find the path.
A minimum priority queue can be used to efficiently receive the vertex with least path distance.
PSEUDOCODE OF DIJKSTRA

8. 1 function Dijkstra(Graph, source):
2
3 create vertex set Q
4
5 for each vertex v in Graph:
6 dist[v] ← INFINITY
7 prev[v] ← UNDEFINED
8 add v to Q
9 dist[source] ← 0
10
11 while Q is not empty:
12 u ← vertex in Q with min dist[u]
13
14 remove u from Q
15
16 for each neighbor v of u still in Q:
17 alt ← dist[u] + length(u, v)
18 if alt < dist[v]:
19 dist[v] ← alt
20 prev[v] ← u
21
22 return dist[], prev[]
PSEUDOCODE

9. CODE FOR DIJKSTRA’S ALGORITHM
The implementation of Dijkstra's Algorithm in C
is given. The complexity of the code can be
improved, but the abstractions are convenient to
relate the code with the algorithm.
Scan this
QR Code using Google Lens to get access to the
drive containing necessary coding files
Log in using College ID

10. Time Complexity: O(E Log V)
where, E is the number of edges and V is the number of vertices.
Space Complexity: O(V)
DIJKSTRA’S ALGORITHM COMPLEXITY

11. APPLICATIONS OF DIJKSTRA’S
ALGORITHM
• To find the shortest path
• In social networking applications
• In a telephone network
• To find the locations in the map

12. CONCLUSION
When the algorithm finishes, each vertex reachable from the
source has v. distance set to the length of the shortest path
from the source, and v. parent set to its parent in the tree of
shortest paths.

13. • https://www.programiz.com/dsa/dijkstra-algorithm
• https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
• https://www.quora.com/What-is-the-conclusion-of-Dijkstras-algorithm
BIBLIOGRAPHY

14. For your precious time towards our
presentation
THANK
YOU!