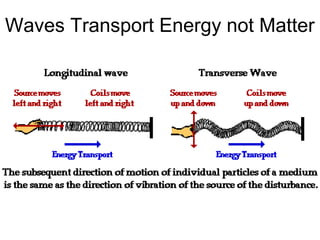
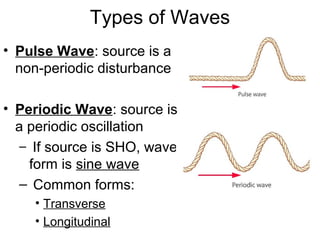
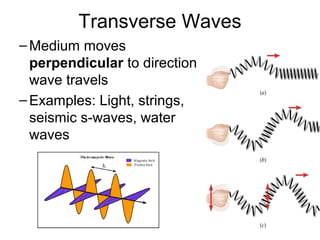
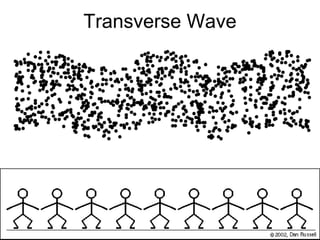
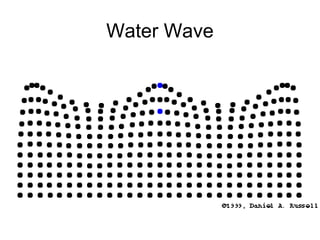
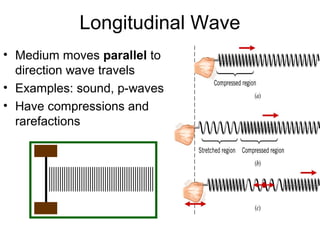
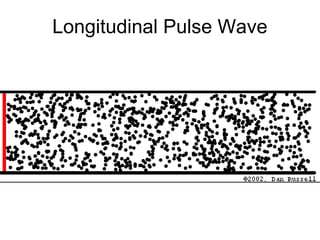
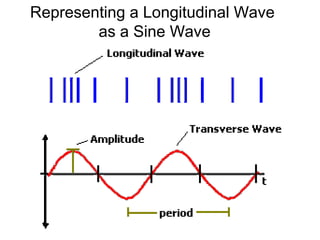
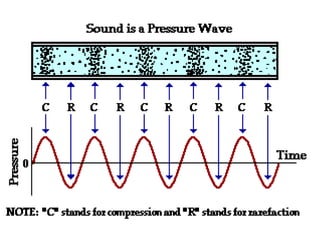
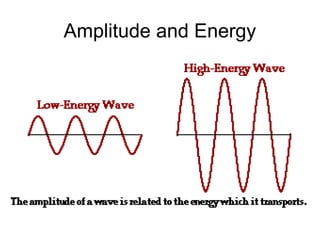
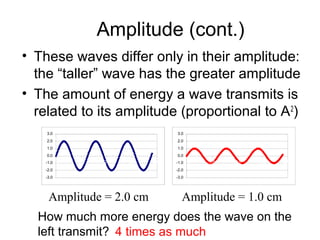
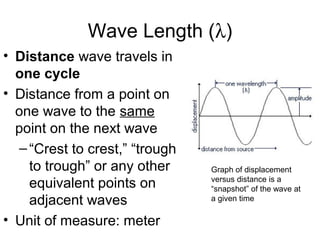
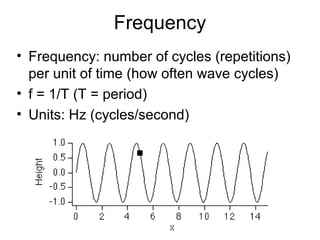
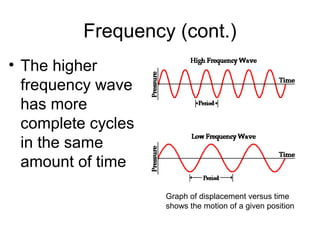
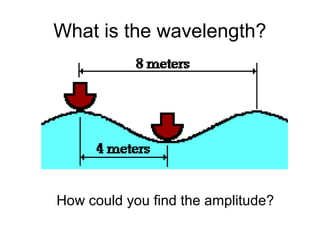
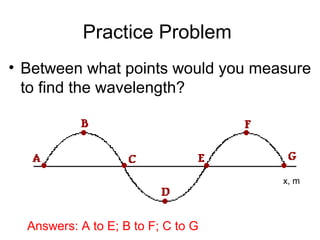
Waves transport energy through a medium rather than matter. There are two main types of waves: transverse waves, where the medium moves perpendicular to the wave's direction of travel, and longitudinal waves, where the medium moves parallel to the direction of travel. Key wave parameters include amplitude, wavelength, frequency, period, and speed. The wavelength is the distance between two equivalent points on consecutive waves, frequency is the number of waves passing a point per second, and speed depends on the properties of the medium and can be calculated as speed equals wavelength times frequency.

1. Introduction to
Waves

2. What is a Wave?
• Wave: motion of a disturbance
– Disturbance creates waves that
travel away from the source of the
disturbance
• Waves transport energy, not matter.
• Mechanical waves require a
medium: the elastic, deformable
matter through which disturbance
travels
• Electromagnetic waves don’t
require a medium

3. Waves Transport Energy not Matter

4. Types of Waves
• Pulse Wave: source is a
non-periodic disturbance
• Periodic Wave: source is
a periodic oscillation
– If source is SHO, wave
form is sine wave
– Common forms:
• Transverse
• Longitudinal

5. Transverse Waves
–Medium moves
perpendicular to direction
wave travels
–Examples: Light, strings,
seismic s-waves, water
waves

6. Transverse Wave

7. Water Wave

8. Longitudinal Wave
• Medium moves parallel to
direction wave travels
• Examples: sound, p-waves
• Have compressions and
rarefactions

9. Longitudinal Waves (cont.)
• Additional terms with longitudinal waves:
• Compression: where wave fronts are
closer together than in undisturbed
medium
• Rarefaction: where they are farther apart
than in undisturbed medium

10. Longitudinal Pulse Wave

11. Representing a Longitudinal Wave
as a Sine Wave

13. Wave Parameters
The following parameters are used to
describe waves:
–Amplitude
–Wave length
–Frequency
–Period
–Speed

14. Amplitude (A)
• How “tall” (or “wide”) the wave is
• Maximum displacement from the average
or equilibrium position
–Crests: highs
–Troughs: lows
–Measured from “crest to rest” or “trough
to rest”
• Unit of measure: meter

15. Amplitude and Energy

16. Amplitude (cont.)
• These waves differ only in their amplitude:
the “taller” wave has the greater amplitude
• The amount of energy a wave transmits is
related to its amplitude (proportional to A2
)
-3.0
-2.0
-1.0
0.0
1.0
2.0
3.0
0.0 5.0 10.0 15.0 20.0
-3.0
-2.0
-1.0
0.0
1.0
2.0
3.0
0.0 5.0 10.0 15.0 20.0
Amplitude = 2.0 cm Amplitude = 1.0 cm
How much more energy does the wave on the
left transmit? 4 times as much

17. Wave Length (λ)
• Distance wave travels in
one cycle
• Distance from a point on
one wave to the same
point on the next wave
–“Crest to crest,” “trough
to trough” or any other
equivalent points on
adjacent waves
• Unit of measure: meter
Graph of displacement
versus distance is a
“snapshot” of the wave at
a given time

18. Parts of the Wave
• Equilibrium – rest position, zero movement
• Crest – top of wave
• Trough – bottom of wave
• Amplitude – height from rest to top or bottom
• Wavelength – distance wave travels in 1 cycle

19. Frequency
• Frequency: number of cycles (repetitions)
per unit of time (how often wave cycles)
• f = 1/T (T = period)
• Units: Hz (cycles/second)

20. Frequency (cont.)
• The higher
frequency wave
has more
complete cycles
in the same
amount of time
Graph of displacement versus time
shows the motion of a given position

21. Period (T)
• Time for one complete wave to pass any
given point
• Unit of measure: seconds
• The period and frequency are reciprocals:
T = 1/f
f = 1/T

22. Wave Speed (v)
• How fast a wave transmits energy from
one place to another
• IMPORTANT: Wave speed depends only
on specific properties of the medium)
• For example:
– Wave in string: tension and density
– Wave in fluid: rigidity and density
– Wave in solid: elasticity and density
• Constant for a given medium at given
conditions
• Changes only if properties of medium do!
• Unit of measure: meter/sec

23. Wave Speed (cont.)
• Wave speeds vary widely:
–Water waves: a few miles per hour
–Sound (in air): about 340 m/sec or 1100
ft/sec (depends on temperature)
–Electromagnetic waves (in vacuum): about
3.0 x 108
meters/sec or 186,000 miles/sec
• Speed of light in a medium is always
lower than that in vacuum

24. Wave Speed, Frequency, and
Wavelength are Related
• These variables are related through the
following equation:
speed (m/s) = frequency (Hz) x wavelength (m)
• Better: the product of f and λ is v
• CAUTION: Remember: wave speed doesn’t
depend on f or λ; it depends on. . .
v = f λ
the properties of the medium it’s
traveling through!

25. Practice Problem
• What does each letter represent,
assuming that the x-axis is position?
• What if the x-axis is time?
A = wavelength; C and E = wavelength/2;
D = amplitude; B = 2 x amplitude
A = period; C and E = period/2;
D = amplitude; B = 2 x amplitude

26. What is the wavelength?
How could you find the amplitude?

27. Practice Problem
• Between what points would you measure
to find the wavelength?
x, m
Answers: A to E; B to F; C to G

28. Wave Properties (cont.)
• Here’s an example transverse wave
showing some of the quantities we’ve
talked about so far:
How many complete wavelengths are shown?
x, m
2