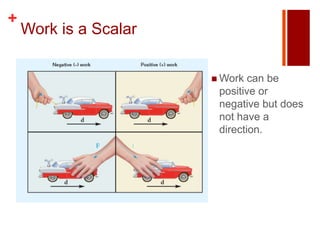
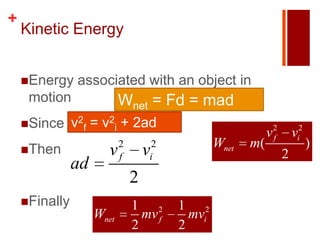
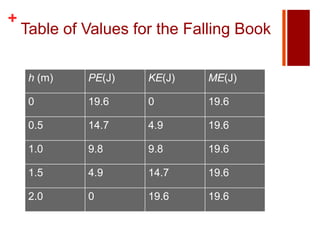
The document discusses work, energy, and the conservation of mechanical energy. It defines work as the product of force and displacement, and introduces kinetic energy as the energy of motion and potential energy as stored energy due to position or force interactions. The document also explains that the total mechanical energy, which is the sum of an object's kinetic and potential energies, remains constant in an isolated system according to the law of conservation of energy.

1. +
Work and Energy
Chapter 5
Pg. 158-181

2. +
5.1 Work
Pg. 160-163

3. +
What do you think?
 List five examples of things you have done in the
last year that you would consider work.
 Based on these examples, how do you define
work?

4. +
Work
 Inphysics, work is the magnitude of the force (F)
times the magnitude of the displacement (d) in
the same direction as the force.
W = Fd
 What are the SI units for work?
 Force units (N) distance units (m)
 N•m are also called joules (J).
 How much work is 1 joule?
 Liftan apple weighing about 1 N from the floor to
the desk, a distance of about 1 m.

5. +
Work
 Pushing this car is work because F and d are in
the same direction.
 Why aren’t the following tasks considered
work?
 A student holds a heavy chair at arm’s length for
several minutes.
 A student carries a bucket of water along
a horizontal path while walking at a
constant velocity.

6. +
Work
 At an angle you can use the below equation
to calculate the work being done
 Ifthe angle is 90°, what is the component of F in
the direction of d?
 Fcos 90° = 0
 Ifthe angle is 0°, what is the component of F in
the direction of d?
 Fcos 0° = F

7. +
Example
 How much work is being done on a
vacuum cleaner pulled 3.0 m by a force of
50.0 N at an angle of 30° above the
horizontal?
 Given:
 F= 50.0N d= 3.0 m θ=30°

8. +
Example
 W=Fdcosθ
 W= (50)(3) cos(30°)
 W= 129.90J

9. +
Classroom Practice Problem
 A 20.0kg suitcase is raised 3.0 m above a
platform. How much work is done on the
suitcase?
 Answer: 5.9 x 102 J or 590 J

10. +
Work is a Scalar
 Work can be
positive or
negative but does
not have a
direction.

11. +
Sign of Work is Important
 Work is positive
 Force is in the same direction as the displacement
 Work is negative
 Forceis in a different direction as the
displacement
 Sign of the net work lets you know if the object
is speeding up or down
+ for speeding up and work is being on object
 - for slowing down and work is done by object

12. +
5.2 Energy
Pg. 164- 172

13. +
What do you think?
 You have no doubt heard the term kinetic energy.
 What is it?
 What factors affect the kinetic energy of an object
and in what way?
 Youhave no doubt heard the term potential
energy.
 What is it?
 What factors affect the potential energy of an object
and in what way?

14. +
Kinetic Energy
Energy associated with an object in
motion Wnet = Fd = mad
Since v2f = v2i + 2ad
v2
f vi2
2 2 Wnet m( )
Then v f v
i 2
ad
2
Finally 1 2 1 2
Wnet mv f mvi
2 2

15. +
Kinetic Energy
Kinetic energy depends on speed and
mass
The net work done on a body equals its
change in kinetic energy
SI units for KE
 kg•m2/s2 or N•m or Joule (J)

16. +
Example
 A 7.0 Kg bowling ball moves at 3.0 m/s. How
fast must a 2.45g ping pong ball move in order
to have the same kinetic energy as the bowling
ball? Is the speed reasonable for the ping
pong ball?
 Given:
 Bowling ball: m= 7.0 kg v= 3.0m/s
 Ping pong: m= 2.45 g (this= 0.00245kg) v=??

17. +
Example
2KE
 KE= ½ mv2 v
m
 KE= ½ (7)(32)
2(31.5)
 KE= 31.5 J v
0.00245
 Rearrange Equation v = 160.36 m/s
to get v by itself

18. +
Classroom Practice Problems
 A 6.00
kg cat runs after a mouse at 10.0
m/s. What is the cat’s kinetic energy?
 Answer: 3.00 x 102 J or 300 J
 Suppose the above cat accelerated to a
speed of 12.0 m/s while chasing the
mouse. How much work was done on the
cat to produce this change in speed?
 Answer: 1.32 x 102 J or 132 J

19. +
Work and Kinetic Energy
 KEis the work an object can do if the speed
changes.
 Wnet is positive if the speed increases.
 You must include all the forces that do work
on the object in calculating the net work done

20. +
Potential Energy
 Energyassociated with an object’s potential
to move due to an interaction with its
environment; basically its stored energy
 A book held above the desk
 An arrow ready to be released from the bow
 Some types of PE are listed below.
 Gravitational
 Elastic
 Electromagnetic

21. +
Gravitational Potential Energy
 Energy associated with an object due to the
object’s position relative to a gravitational
source
 SI unit is still a Joule
 Theheight (h) depends on the “zero level”
chosen where PEg= 0.

22. +
Elastic Potential Energy
 Theenergy available for use in deformed elastic
objects
 Rubber bands, springs in trampolines, pole-vault poles,
muscles
 For springs, the distance compressed or stretched =
x

23. +
Elastic Potential Energy
The spring constant (k) depends on the
stiffness of the spring.
 Stiffer
springs have higher k values.
 Measured in N/m
 Force in newtons needed to stretch a spring 1.0
meters

24. +
Example
 A 70.0kg stuntman is attached to a bungee
cord with an unstretched length of 15m. He
jumps off a bridge from a height of 50m.
When he finally stops the cord has a
stretched length of 44m. Assuming the spring
constant is 71.8 N/m, what is the total PE
relative to the water when the man stops
falling?

25. +
Example
 Given:
 m= 70kg k= 71.8 N/m g= 10m/s2
 h= 50m – 44m= 6m
 x= 44m – 15m= 29m
 PEg= mgh
 PEelastic = ½ k x2
 PEtotal= PEg + PEelastic

26. +
Example
 PEg= mgh  PEelastic = ½ k x2
 PEg= (70)(10)(6)  PEelastic= ½ (71.8)(292)
 PEg= 4200 J  PEelastic= 30191.9J
 PEtotal= PEg + PEelastic
 PEtotal= 4200 + 30191.9
 PEtotal= 34391.9J

27. +
Classroom Practice Problems
 When a 2.00 kg mass is attached to a
vertical spring, the spring is stretched 10.0
cm such that the mass is 50.0 cm above the
table.
 What is the gravitational potential energy
associated with the mass relative to the table?
 Answer: 9.81 J
 What is the spring’s elastic potential energy if
the spring constant is 400.0 N/m?
 Answer: 2.00 J

28. +
5.3 Conservation of Energy
Pg. 173-178

29. +
What do you think?
 Imagine two students standing side by side at the
top of a water slide. One steps off of the platform,
falling directly into the water below. The other
student goes down the slide. Assuming the slide
is frictionless, which student strikes the water
with a greater speed?
 Explain your reasoning.
 Would your answer change if the slide were not
frictionless? If so, how?

30. +
What do you think?
 What is meant when scientists say a quantity
is conserved?
 Describe
examples of quantities that are
conserved.
 Are they always conserved? If not, why?

31. +
Mechanical Energy (ME)
 ME = KE + PEg + PEelastic
 Doesnot include the many other types of
energy, such as thermal energy, chemical
potential energy, and others
 ME is not a new form of energy.
 Just a combination of KE and PE

32. +
Conservation of Mechanical Energy
 The sum of KE and PE remains constant.
 One type of energy changes into another
type.
 For the falling book, the PE of the book changed
into KE as it fell.
 As a ball rolls up a hill, KE is changed into PE.

33. +
Example
 Starting from rest, a child zooms down a
frictionless slide from an initial height of
3.0m. What is her speed at the bottom of
the slide? Her mass is 25kg.
 Given:
 vi= 0m/s hi= 3m m=25kg
 vf= ?? hf=0m

34. +
Example
*Choose your equations
 PE= mgh  KE= ½ mv2
 PEf= (25)(10)(0)  KEf= ½ (25)v2
 PEf= 0J  KEf= ??
 PEi= (25)(10)(3)  KEi= ½ (25)(02)
 PEi= 750J  KEi= 0J

35. +
Example
*Put together
 PEi+ KEi= PEf+ KEf
 750 + 0 = 0 + ½ (25)vf2
 750= 12.5 vf2
 vf2 = √60
 vf= 7.75m/s

36. +
Classroom Practice Problems
 Suppose a 1.00 kg book is dropped from a height
of 2.00 m. Assume no air resistance.
 Calculate the PE and the KE at the instant the book
is released.
 Answer: PE = 19.6 J, KE = 0 J
 Calculate the KE and PE when the book has fallen
1.0 m. (Hint: you will need an equation from Chapter
2.)
 Answer: PE = 9.81 J, KE = 9.81 J
 Calculate the PE and the KE just as the book
reaches the floor.
 Answer: PE = 0 J, KE = 19.6 J

37. +
Table of Values for the Falling Book
h (m) PE(J) KE(J) ME(J)
0 19.6 0 19.6
0.5 14.7 4.9 19.6
1.0 9.8 9.8 19.6
1.5 4.9 14.7 19.6
2.0 0 19.6 19.6

38. +
Conservation of Energy
 Acceleration does not have to be constant.
 ME is not conserved if friction is present.
 If friction is negligible, conservation of ME is reasonably
accurate.
 A pendulum as it swings back and forth a few times
 Consider a child going down a slide with friction.
 What happens to the ME as he slides down?
 Answer: It is not conserved but, instead, becomes less
and less.
 The “lost” energy? is converted into nonmechanical
energy (thermal energy).

39. +
Classroom Practice Problems
 A small 10.0 g ball is held to a slingshot that
is stretched 6.0 cm. The spring constant is
2.0 102 N/m.
 What is the elastic potential energy of the
slingshot before release?
 What is the kinetic energy of the ball right after
the slingshot is released?
 What is the ball’s speed at the instant it leaves
the slingshot?
 How high does the ball rise if it is shot directly
upward?

40. +
Now what do you think?
 Imagine two students standing side by side at the
top of a water slide. One steps off of the platform,
falling directly into the water below. The other
student goes down the slide. Assuming the slide
is frictionless, which student strikes the water
with a greater speed?
 Explain your reasoning.
 Would your answer change if the slide were not
frictionless? If so, how?

41. +
Now what do you think?
 What is meant when scientists say a quantity
is “conserved”?
 Describe
examples of quantities that are
conserved.
 Are they always conserved? If not, why?

42. +
5.4 Power
Pg. 179-181

43. +
What do you think?
 Twocars are identical with one exception.
One of the cars has a more powerful engine.
How does having more power make the car
behave differently?
 What does power mean?
 What units are used to measure power?

44. +
Power
Therate at which work is done or
energy is transferred
 Energy used or work done per second
 If we substitute W for Fd then Fd
P
t

45. +
Power
 SI units for power are J/s.
 Calledwatts (W)
 Equivalent to kg•m2/s3
 Horsepower (hp) is a unit used in the
Avoirdupois system.
 1.00 hp = 746 W

46. +
Watts
 These bulbs all consume
different amounts of power.
 A 100watt bulb consumes
100 joules of energy every
second.

47. +
Example
 A 193kg curtain need to be raised 7.5m, at a
constant speed, in as close to 5 sec as
possible. Unsure which motor would be the
best 3 motors were bought. Power ratings are
1.0kW, 3.5kW, and 5.5kW. Which motor is
best for the job?
 Given:
 m= 193kg d= 7.5m t= 5 sec P=??

48. +
Example
W Fd mgd
P
t t t
(193)(10)(7.5)
P
5
 P=2895 W or 2.895kW
 So
the best motor would be the 3.5kW
motor

49. +
Classroom Practice Problems
 Two horses pull a cart. Each exerts a
force of 250.0 N at a speed of 2.0 m/s for
10.0 min.
 Calculate the power delivered by the
horses.
 How much work is done by the two horses?
 Answers: 1.0 x 103 W and 6.0 x 105 J

50. +
Now what do you think?
 Twocars are identical with one exception.
One of the cars has a more powerful engine.
How does having more power make the car
behave differently?
 What does power mean?
 What units are used to measure power?