Download to read offline
Uploaded byazn_punkyfish07
PPTX, PDF315 views
The Calculus Crusaders Volume
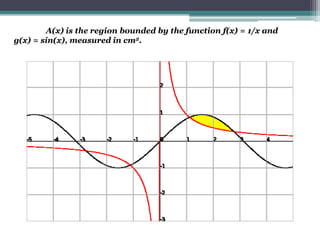
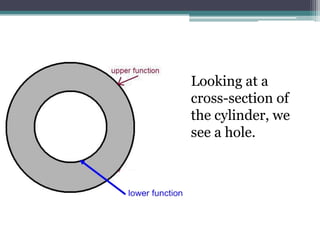
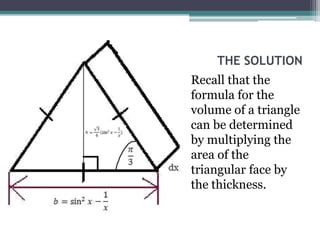
Zeph notices that a duck's turd covers an area on the sand equivalent to the shaded region R in a graph. The region R is bounded by the functions f(x) = 1/x and g(x) = sin(x) between the points they intersect, x = 1.1141571 and x = 2.7726047. Zeph is asked to determine the area of R, the volume when R is revolved about the y-axis, and the volume when R is used as the base for a solid where each cross-section is an equilateral triangle.
