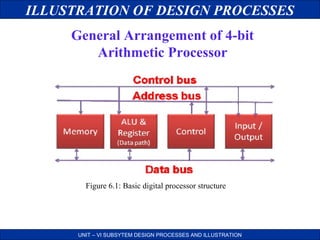
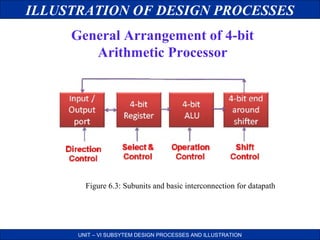
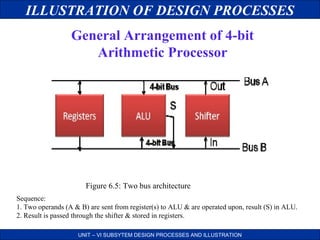
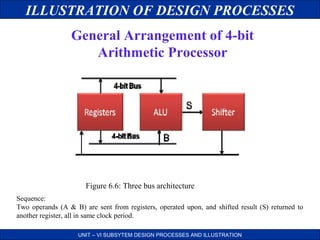
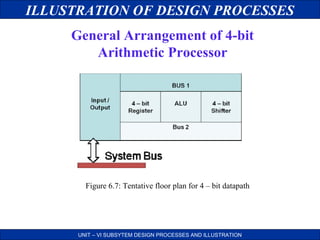
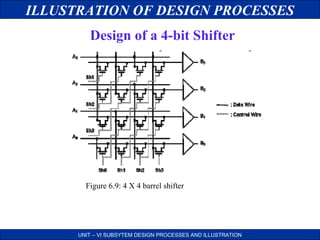
This document discusses the design processes for digital subsystem design. It begins by outlining the objectives of design consideration, problem and solution, basic digital processor structure, and datapath. It then discusses general considerations for subsystem design such as lower unit cost and higher reliability. It presents some common problems in design like how to design complex systems efficiently. It proposes solutions like top-down design and partitioning the system. The document then illustrates the design processes through examples like designing a 4-bit shifter and ALU subsystem. It provides block diagrams, logic diagrams and layouts at different stages of the design process.






















![COMPUTATIONAL ELEMENTS
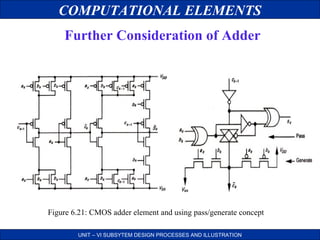
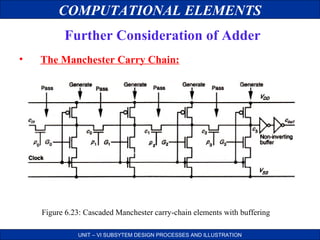
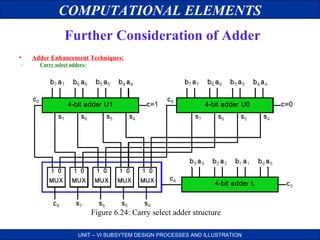
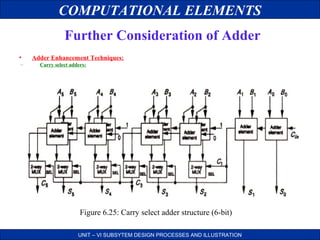
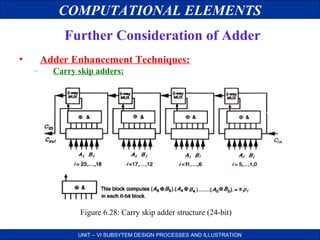
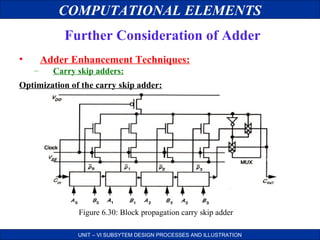
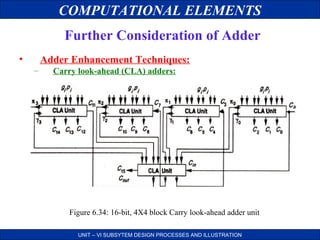
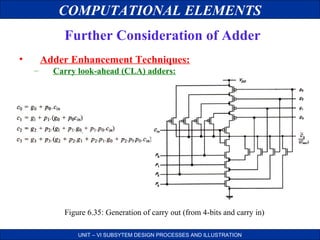
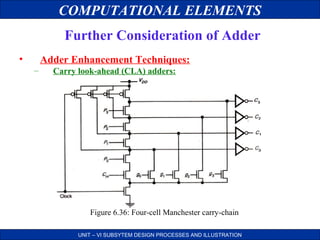
Further Consideration of Adder
Generation:
• This principle of generation allows the system to take
advantage of the occurrences “Ak=Bk”.
Propagation:
• If we are able to localize a chain of bits Ak Ak+1... Ak+p and Bk
Bk+1... Bk+p for which Ak not equal to Bk for k in [k, k+p], then the
output carry bit of this chain will be equal to the input carry bit
of the chain.
• These remarks constitute the principle of generation and
propagation used to speed the addition of two numbers.
• All adders which use this principle calculate in a first stage.
Pk = Ak XOR Bk
Gk = Ak Bk
UNIT – VI SUBSYTEM DESIGN PROCESSES AND ILLUSTRATION](https://image.slidesharecdn.com/vlsisubsystemdesignprocessesandillustration-131101063110-phpapp02/85/VLSI-subsystem-design-processes-and-illustration-33-320.jpg)