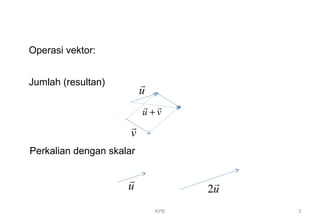
1. Dokumen membahas tentang vektor, termasuk definisi vektor, operasi vektor seperti jumlah vektor dan perkalian vektor dengan skalar, norma vektor, hasil kali titik dan silang dua vektor, proyeksi vektor, divergensi dan curl medan vektor, serta gradien medan skalar.
2. Berisi contoh soal dan penyelesaian tentang operasi vektor seperti hasil kali titik dua vektor, proyeksi vekt