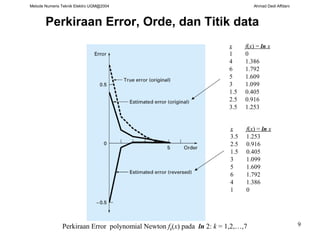
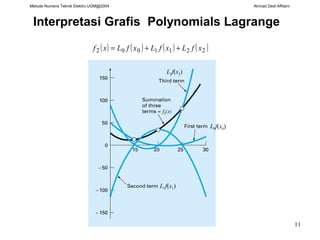
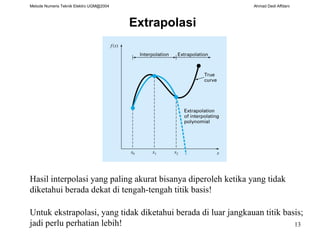
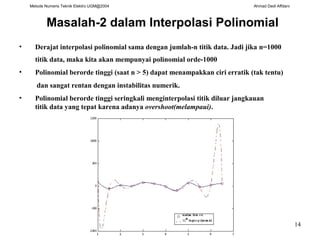
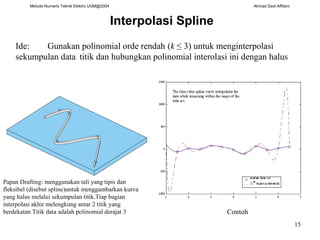
Dokumen ini membahas berbagai metode interpolasi dalam teknik elektro, termasuk interpolasi linear, kuadratik, polynomial Newton, dan spline. Setiap metode dijelaskan dengan formula dan contoh aplikasi untuk memperkirakan nilai fungsi pada titik tertentu. Selain itu, dikemukakan bahwa polinomial berorde tinggi dapat menimbulkan masalah stabilitas numerik saat interpolasi dilakukan dengan banyak titik data.

1. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
1
Bab 4
Interpolasi Newton

2. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
2
Interpolasi Polinomial
Diketahui:n titik data (x1, y1), (x2, y2), … (xn, yn)
Ditanya :a0, a1, …, an sehingga
Dua titik data : Garis
Tiga titik data : Kuadratik
Empat titik data :Polinomial tingkat-3
…
n titik data :Polinomial tingkat-n
( ) n
n xaxaxaaxf ++++= 2
210
02
2
1
0222
2
212
0112
2
111
ayaxaxax
ayaxaxax
ayaxaxax
nn
n
nnn
n
n
n
n
−=+++
−=+++
−=+++
...
...
...

Adakah cara yang lebih baik untuk menyelesaikan persamaan diatas?

3. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
3
Interpolasi Linear
( ) ( )
( ) ( )
( )0
01
01
01 xx
xx
xfxf
xfxf −
−
−
+=
Diketahui: Dua titik(x1, y1), (x2, y2)
Ditanya :Garis yang melewati 2 titik tersebut
Contoh: f(x) = ln x
x1 = 1 dan x2 = 6:
f1(2) = 0.3583519
x1 = 1 dan x2 = 4
f1(2) = 0.4620981
ln 2 = 0.6931472
Semakin kecil intervalnya semakin baik hasil interpolasi!

4. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
4
Interpolasi Kuadratis
( )
( ) ( )
( ) ( ) ( ) ( )
02
01
01
12
12
2
01
01
100
xx
xx
xfxf
xx
xfxf
b
xx
xfxf
bxfb
−
−
−
−
−
−
=
−
−
==
( ) ( ) ( )( )1020102 xxxxbxxbbxf −−+−+=
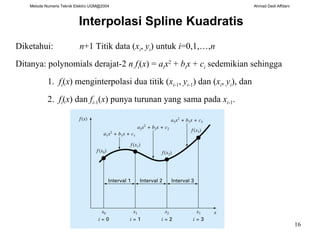
Diketahui: Tiga titik(x1, y1), (x2, y2), (x3,y3)
Ditanya: kuadratis f2(x) = a0 + a1x + a2x2
yang melewati ke-3 titik diatas
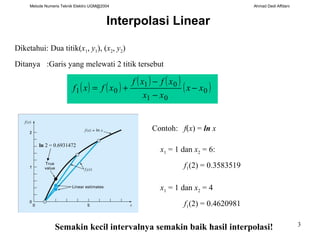
Contoh: f(x) = ln x
Titik data: (1, 0), (4, 1.386294), (6, 1.791759)
b0 = 0
b1 = (1.386294 – 0)/(4 – 1) = 0.4620981
b2 = [(1.791759 – 1.386294)/(6-4) – 0.4620981]/(6-1)
= -0.0518731
f2(2) = 0.5658444
ln 2 = 0.6931472

5. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
5
Interpolasi Polynomial Newton
( )
[ ]
[ ]011
011
00
xxxxfb
xxfb
xfb
nnn ,,,
,


−=
=
=
( ) ( ) ( )( ) ( )( ) ( )110102010 −−−−++−−+−+= nnn xxxxxxbxxxxbxxbbxf ...
[ ] ( ) ( )
ji
ji
ji
xx
xfxf
xxf
−
−
=,
Diketahui: n titik (x1, y1), (x2, y2), …, (xn, yn) (yi = f(xi), i=1,2,…,n)
Ditanya: fn(x) = a0 + a1x + a2x2
+ … + anxn
yang melewati n titik tersebut.
dengan
[ ] [ ] [ ]
ki
kjji
kji
xx
xxfxxf
xxxf
−
−
=
,,
,,
[ ] [ ] [ ]
0
02111
011
,...,,,...,,
,,...,,
xx
xxxfxxxf
xxxxf
n
nnnn
nn
−
−
= −−−
−
Rekursif!

6. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
6
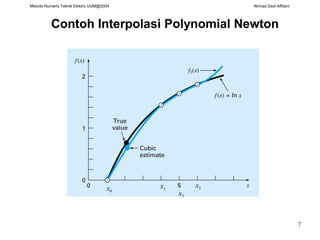
Contoh Interpolasi Polynomial Newton
( ) ( ) ( )( ) ( )( ) ( )( )( )2103102102010 xxxxxxbxxxxbxxxxbxxbbxfn −−−+−−+−−+−+=
[ ] [ ] [ ] 182.0
65
791759.1609438.1
,203.0
46
386294.1791759.1
,462.0
14
0386294.1
, 231201 =
−
−
==
−
−
==
−
−
= xxfxxfxxf
[ ] [ ] 0200
45
20301820
0520
16
46202030
123012 .
..
,,.
..
,, −=
−
−
=−=
−
−
= xxxfxxxf
Diketahui: (1, 0), (4, 1.386294), (6, 1.791759), (5, 1.609438) (dari fungsi ln x)
Ditanya: Perkirakan ln 2 dengan interpolasi Newton orde ke-3
f3(2) = 0.629
[ ] 0080
15
)0520(0200
0123 .
..
,,, =
−
−−−
=xxxxf

7. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
7
Contoh Interpolasi Polynomial Newton
x0
x1
x3
x2

8. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
8
Perkiraan Error Polynomial Newton
( ) ( )
( )
( ) 1
1
1
1
+
+
+
−
+
= n
ii
n
n xx
n
f
R
!
ξ
( ) ( )
( )
( )( )( ) ( )n
n
n xxxxxxxx
n
f
R −−−−
+
=
+
210
1
1 !
ξ
( ) ( ) ( )( ) ( )( ) ( )110102010 −−−−++−−+−+= nnn xxxxxxbxxxxbxxbbxf ...
Jika f(x) dinyatakan oleh deret Taylor , error setelah terms ke-n adalah:
Untuk suatui polinomial Newton orde ke-n, Hubungan untuk error scr analogi:
Tapi kita tidak tahu apakah itu f(x)! Sebagai suatu perkiraan untuk error, bisa
kita gunakan
[ ]( )( )( ) ( )nnnnn xxxxxxxxxxxxfR −−−−≅ −+  210011 ,,,,
(Ingat: fn+1(x) = fn(x) + Rn)

9. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
9
Perkiraan Error, Orde, dan Titik data
x f(x) = ln x
1 0
4 1.386
6 1.792
5 1.609
3 1.099
1.5 0.405
2.5 0.916
3.5 1.253
Perkiraan Error polynomial Newton fk(x) pada ln 2: k = 1,2,…,7
x f(x) = ln x
3.5 1.253
2.5 0.916
1.5 0.405
3 1.099
5 1.609
6 1.792
4 1.386
1 0

10. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
10
Polinomial Interpolasi Lagrange
( ) ∏
−
−
=
≠
=
n
ij
j ji
i
i
xx
xx
xL
0
( ) ( ) ( )1
01
0
0
10
1
1:linear xf
xx
xx
xf
xx
xx
xf
−
−
+
−
−
=
dengan
( ) ( ) ( )i
n
i
in xfxLxf ∑=
=0
Contoh:
( ) ( )( )
( )( )
( )
( )( )
( )( )
( )
( )( )
( )( )
( )2
1202
10
1
2101
20
0
010
21
2
2
:order-2nd xf
xxxx
xxxx
xf
xxxx
xxxx
xf
xxxx
xxxx
xf
−−
−−
+
−−
−−
+
−−
−−
=

11. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
11
Interpretasi Grafis Polynomials Lagrange
( ) ( ) ( ) ( )2211002 xfLxfLxfLxf ++=
L0f(x0)
L1f(x1)
L2f(x2)

12. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
12
Interpolasi Inverse
x
x
y
Interpolated point of (xc, f(xc))
Interpolated curve
true curve
fn(x) = a0 + a1x + a2x2
+ … + anxn interpolasi yc = fn(xc)
Bagimana inverse-nya:
fn(y) = a0 + a1y + a2y2
+ … + anyn
interpolasi xc = fn(yc)
Keduanya tidak ekuivalen dalam hal keakuratan interpolasi!

13. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
13
Extrapolasi
Hasil interpolasi yang paling akurat bisanya diperoleh ketika yang tidak
diketahui berada dekat di tengah-tengah titik basis!
Untuk ekstrapolasi, yang tidak diketahui berada di luar jangkauan titik basis;
jadi perlu perhatian lebih!

14. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
14
Masalah-2 dalam Interpolasi Polinomial
• Derajat interpolasi polinomial sama dengan jumlah-n titik data. Jadi jika n=1000
titik data, maka kita akan mempunyai polinomial orde-1000
• Polinomial berorde tinggi (saat n > 5) dapat menampakkan ciri erratik (tak tentu)
dan sangat rentan dengan instabilitas numerik.
• Polinomial berorde tinggi seringkali menginterpolasi titik diluar jangkauan
titik data yang tepat karena adanya overshoot(melampaui).

15. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
15
Interpolasi Spline
Ide: Gunakan polinomial orde rendah (k ≤ 3) untuk menginterpolasi
sekumpulan data titik dan hubungkan polinomial interolasi ini dengan halus
Papan Drafting: menggunakan tali yang tipis dan
fleksibel (disebut spline)untuk menggambarkan kurva
yang halus melalui sekumpulan titik.Tiap bagian
interpolasi akhir melengkung antar 2 titik yang
berdekatan Titik data adalah polinomial derajat 3 Contoh

16. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
16
Interpolasi Spline Kuadratis
Diketahui: n+1 Titik data (xi, yi) untuk i=0,1,…,n
Ditanya: polynomials derajat-2 n fi(x) = aix2
+ bix + ci sedemikian sehingga
1. fi(x) menginterpolasi dua titik (xi-1, yi-1) dan (xi, yi), dan
2. fi(x) dan fi-1(x) punya turunan yang sama pada xi-1.

17. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
17
Turunan Quadratic Spline
1. fi-1(xi-1) = ai-1xi-1
2
+ bi-1xi-1 + ci-1 = yi-1
fi(xi-1) = aixi-1
2
+ bixi-1 + ci = yi-1
2n – 2 persamaan
2. f1(x0) = a1x0
2
+ b1x0 + c1 = y0
fn(xn) = anxn
2
+ bnxn + cn = yn
2 persamaan
3. (the 1st
derivative at the interior knots must be equal)
fi-1’(xi-1) = 2ai-1xi-1 + bi-1 = 2aixi-1 + bi = fi’(xi-1) n– 1 persamaan

18. Metode Numeris Teknik Elektro UGM@2004 Ahmad Dedi Affdani
18
Contoh of Quadratic Spline