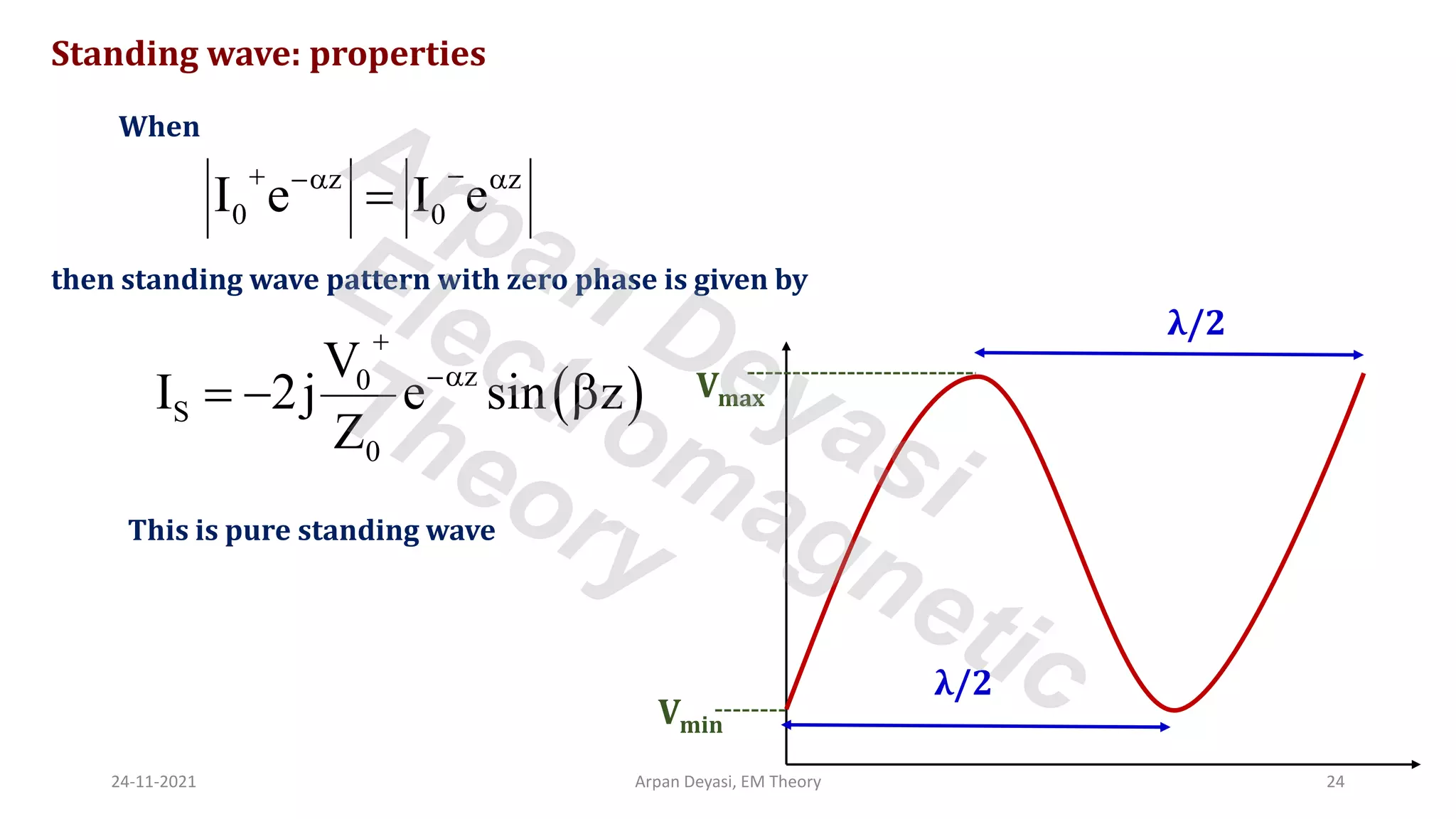
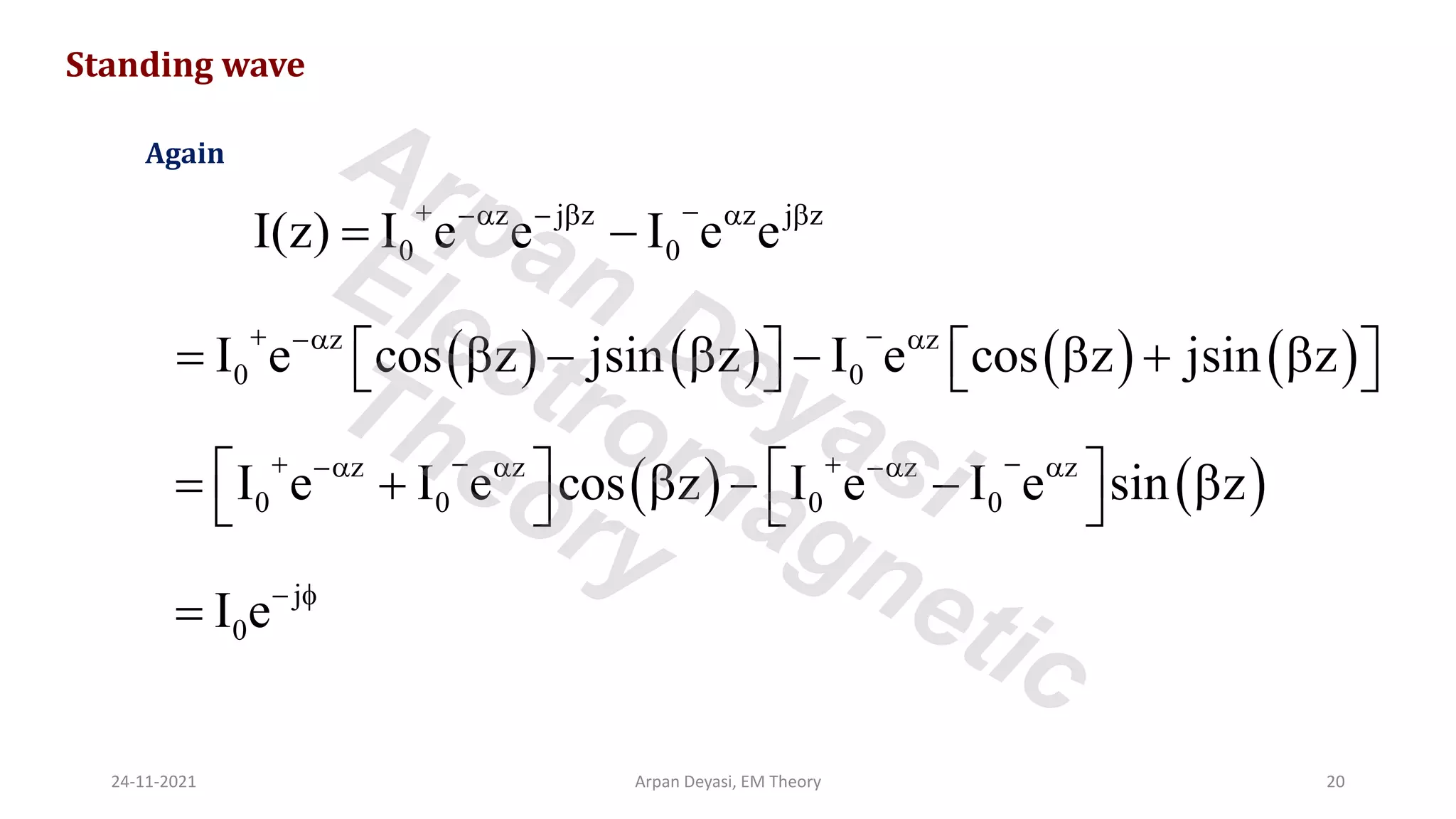This document discusses transmission line propagation coefficients including reflection coefficient and transmission coefficient. It defines the reflection coefficient as the ratio of reflected to incident voltage or current. Reflection and transmission coefficients are derived for a transmission line terminated by a load impedance. Standing wave patterns on transmission lines are also analyzed. Key properties of standing waves include maximum and minimum voltages occurring at intervals of half wavelength and voltages/currents being 90 degrees out of phase.

1. Course: Electromagnetic Theory
paper code: EI 503
Course Coordinator: Arpan Deyasi
Department of Electronics and Communication Engineering
RCC Institute of Information Technology
Kolkata, India
Topic: Transmission Line – Propagation Coefficients
24-11-2021 Arpan Deyasi, EM Theory 1
Arpan Deyasi
Electromagnetic
Theory

2. Reflection Coefficient
It is the ratio of reflected voltage(/current) with the incident voltage (/current)
for a given transmission line
ref ref
inc inc
V I
V I
 = = −
z
z 0 inc
inc 0
0 0
V e V
I I e
Z Z
+ −
+ −
= = =
z
z 0 ref
ref 0
0 0
V e V
I I e
Z Z
− 
− 
= = − = −
24-11-2021 Arpan Deyasi, EM Theory 2
Arpan Deyasi
Electromagnetic
Theory

3. Reflection Coefficient
z z
0 0
V(z) V e V e
+ −
− 
= +
Now
z z
0 0
V(z) V e V e
+ +
− −
= + 
( )
z
0
V(z) V e 1
+ −
= + 
24-11-2021 Arpan Deyasi, EM Theory 3
Arpan Deyasi
Electromagnetic
Theory

4. Reflection Coefficient
Similarly
z z
0 0
I(z) I e I e
+ −
− 
= −
z z
0 0
I(z) I e I e
+ +
− −
= − 
( )
z
0
I(z) I e 1
+ −
= − 
24-11-2021 Arpan Deyasi, EM Theory 4
Arpan Deyasi
Electromagnetic
Theory

5. Reflection Coefficient
If the transmission line has a length ‘l’
( )
l
0 l
V(l) V e 1
+ −
= + 
( )
l
0 l
I(l) I e 1
+ −
= − 
24-11-2021 Arpan Deyasi, EM Theory 5
Arpan Deyasi
Electromagnetic
Theory

6. Reflection Coefficient
If the transmission line is terminated by load ‘ZL’
( )
( )
l
0 l
l
0 l
V e 1
V(l)
Z(l)
I(l) I e 1
+ −
+ −
+ 
= =
− 
( )
( )
l
0
l
1
Z(l) Z
1
+ 
=
− 
L 0
l
L 0
Z Z
Z Z
−
 =
+
24-11-2021 Arpan Deyasi, EM Theory 6
Arpan Deyasi
Electromagnetic
Theory

7. Tranmission Coefficient
Transmission coefficient
tr tr
inc inc
V I
T
V I
= =
L 0
L 0
Z Z
T 1 1
Z Z
−
= +  = +
+
L
L 0
2Z
T
Z Z
=
+
24-11-2021 Arpan Deyasi, EM Theory 7
Arpan Deyasi
Electromagnetic
Theory

8. Transmission Coefficient
From power conservation principle
in ref tr
P P P
= +
tr in ref
P P P
= −
( ) ( ) ( )
2 2 2
l l l
tr 0 0
L 0 0
V e V e V e
2Z 2Z 2Z
+ + −
− − −
= −
24-11-2021 Arpan Deyasi, EM Theory 8
Arpan Deyasi
Electromagnetic
Theory

9. Transmission Coefficient
( ) ( ) ( )
( )
2 2 2
l l l
tr 0 0
2
l
L 0
0
V e V e V e
1
2Z 2Z V e
+ + −
− − −
+ −
 
 
= −
 
 
 
2
2 L
l
0
Z
T 1
Z
 
= − 
 
24-11-2021 Arpan Deyasi, EM Theory 9
Arpan Deyasi
Electromagnetic
Theory

10. Problem 1
A certain transmission line has characteristic impedance (75+j0.01) Ω and is
terminated by load impedance of (70+j50) Ω. Calculate reflection coefficient
and transmission coefficient.
Soln
L 0
l
L 0
Z Z
Z Z
−
 =
+
l
(70 j50) (75 j0.01)
(70 j50) (75 j0.01)
+ − +
 =
+ + +
l 0.08 j0.32
 = +
24-11-2021 Arpan Deyasi, EM Theory 10
Arpan Deyasi
Electromagnetic
Theory

11. T 1
= + 
T 1 0.08 j0.32
= + +
T 1.08 j0.32
= +
24-11-2021 Arpan Deyasi, EM Theory 11
Arpan Deyasi
Electromagnetic
Theory

12. Problem 2
A lossless transmission line has characteristic impedance 50 Ω and is terminated by
load impedance of 75 Ω. If the line is energized by a generator with output impedance
of 50 Ω and open circuit output voltage of 30 V [rms). Find magnitude of instantaneous
load voltage, instantaneous power delivered to the load. Consider length of the line is
2.25λ.
Soln
2
l .
4 2
  
 = =

L 0
l
L 0
Z Z 75 50
0.2
Z Z 75 50
− −
 = = =
+ +
24-11-2021 Arpan Deyasi, EM Theory 12
Arpan Deyasi
Electromagnetic
Theory

13. Instantaneous voltage at load
( )
l
0 l
V(l) V e 1
+ −
= + 
( )
j l
0 l
V(l) V e 1
+ − 
= + 
( )
V(l) 30 1 0.2
= +
V(l) 36 V
=
24-11-2021 Arpan Deyasi, EM Theory 13
Arpan Deyasi
Electromagnetic
Theory

14. Instantaneous power delivered
2
l
L
V
P(l)
Z
=
2
36
P(l)
75
=
P(l) 17.28 W
=
24-11-2021 Arpan Deyasi, EM Theory 14
Arpan Deyasi
Electromagnetic
Theory

15. Standing wave
General solution of transmission line equation
z z
0 0
V(z) V e V e
+ −
− 
= +
z z
0 0
I(z) I e I e
+ −
− 
= −
j
 =  + 
Propagation constant
z z
0 0
V(z) V e V e
+ −
− 
= +
z j z z j z
0 0
I(z) I e e I e e
+ −
− −   
= −
z j z z j z
0 0
V(z) V e e V e e
+ −
− −   
 = +
24-11-2021 Arpan Deyasi, EM Theory 15
Arpan Deyasi
Electromagnetic
Theory

16. z j z z j z
0 0
V(z) V e e V e e
+ −
− −   
= +
Standing wave
Now
( ) ( ) ( ) ( )
z z
0 0
V e cos z jsin z V e cos z jsin z
+ −
− 
=  −  +  + 
   
   
( ) ( )
z z z z
0 0 0 0
V e V e cos z V e V e sin z
+ − + −
−  − 
   
= +  + − 
   
j
0
V e− 
=
24-11-2021 Arpan Deyasi, EM Theory 16
Arpan Deyasi
Electromagnetic
Theory

17. Standing wave
where
( ) ( )
1/ 2
2 2
z z 2 z z 2
0 0 0 0 0
V V e V e cos z V e V e sin z
+ − + −
−  − 
 
   
= +  + − 
   
 
 
( )
( )
( )
z z
0 0
1
z z
0 0
V e V e
tan tan z
V e V e
+ −
− 
−
+ −
− 
 
−
 
 = 
 
+
 
Voltage for
standing-wave pattern
Phase for standing-wave pattern
24-11-2021 Arpan Deyasi, EM Theory 17
Arpan Deyasi
Electromagnetic
Theory

18. Standing wave: properties
Maximum voltage amplitude
z z
max 0 0
V V e V e
+ −
− 
= +
 
z
max 0
V V e 1
+ −
= + 
Minimum voltage amplitude
z z
min 0 0
V V e V e
+ −
− 
= −
 
z
min 0
V V e 1
+ −
= − 
occurs at z n
 = 
occurs at z (2n 1)
2

 = −
24-11-2021 Arpan Deyasi, EM Theory 18
Arpan Deyasi
Electromagnetic
Theory

19. Standing wave: properties
The distance between two successive minima or maxima is one-half wavelength
z n
 = 
n n
z
2
 
= =



n
z
2

=
24-11-2021 Arpan Deyasi, EM Theory 19
Arpan Deyasi
Electromagnetic
Theory

20. Standing wave
z j z z j z
0 0
I(z) I e e I e e
+ −
− −   
= −
Again
( ) ( ) ( ) ( )
z z
0 0
I e cos z jsin z I e cos z jsin z
+ −
− 
=  −  −  + 
   
   
( ) ( )
z z z z
0 0 0 0
I e I e cos z I e I e sin z
+ − + −
−  − 
   
= +  − − 
   
j
0
I e− 
=
24-11-2021 Arpan Deyasi, EM Theory 20
Arpan Deyasi
Electromagnetic
Theory

21. Standing wave
where
( ) ( )
1/ 2
2 2
z z 2 z z 2
0 0 0 0 0
I I e I e cos z I e I e sin z
+ − + −
−  − 
 
   
= −  + + 
   
 
 
( )
( )
( )
z z
0 0
1
z z
0 0
I e I e
tan tan z
I e I e
+ −
− 
−
+ −
− 
 
+
 
 = 
 
−
 
Current for
standing-wave pattern
Phase for standing-wave pattern
24-11-2021 Arpan Deyasi, EM Theory 21
Arpan Deyasi
Electromagnetic
Theory

22. Standing wave: properties
Maximum voltage amplitude
Minimum voltage amplitude
occurs at
occurs at
z z
max 0 0
I I e I e
+ −
− 
= −
 
z
max 0
I I e 1
+ −
= +  z n
 = 
z z
min 0 0
I I e I e
+ −
− 
= +
 
z
min 0
I I e 1
+ −
= −  z (2n 1)
2

 = −
24-11-2021 Arpan Deyasi, EM Theory 22
Arpan Deyasi
Electromagnetic
Theory

23. Standing wave: properties
When
z z
0 0
V e V e
+ −
− 
=
then standing wave pattern with zero phase is given by
( )
z
S 0
V 2V e cos z
+ −
= 
This is pure standing wave
Vmax
Vmin
λ/2
λ/2
24-11-2021 Arpan Deyasi, EM Theory 23
Arpan Deyasi
Electromagnetic
Theory

24. When
z z
0 0
I e I e
+ −
− 
=
then standing wave pattern with zero phase is given by
( )
z
0
S
0
V
I 2j e sin z
Z
+
−
= − 
This is pure standing wave
Standing wave: properties
Vmax
Vmin
λ/2
λ/2
24-11-2021 Arpan Deyasi, EM Theory 24
Arpan Deyasi
Electromagnetic
Theory

25. Voltage and current standing waves are 90° out of phase along any time
Standing wave: properties
Voltage nodes and current nodes are interlaced a quarter-wavelength apart
V I
λ/4
24-11-2021 Arpan Deyasi, EM Theory 25
Arpan Deyasi
Electromagnetic
Theory

26. Standing Wave Ratio
It is the ratio of maximum standing wave pattern (voltage/ current) to the minimum of
that value (voltage/ current)
max max
min min
V I
SWR
V I
= =
1
SWR
1
+ 
=
− 
24-11-2021 Arpan Deyasi, EM Theory 26
Arpan Deyasi
Electromagnetic
Theory

27. 24-11-2021 Arpan Deyasi, EM Theory 27
Problem 3
A transmission line has characteristic impedance (50+j0.01) Ω and is terminated by
load impedance of (73-j42.5) Ω. Calculate SWR.
Soln
L 0
l
L 0
Z Z
Z Z
−
 =
+
l
(73 j42.5) (50 j0.01)
(73 j42.5) (50 j0.01)
− − +
 =
− + +
l 0.377 42.7
 =  
Arpan Deyasi
Electromagnetic
Theory

28. 24-11-2021 Arpan Deyasi, EM Theory 28
1
SWR
1
+ 
=
− 
1 0.377
SWR
1 0.377
+
=
−
SWR 2.21
=
Arpan Deyasi
Electromagnetic
Theory

29. 24-11-2021 Arpan Deyasi, EM Theory 29
Problem 4
Soln
A transmission line of characteristics impedance of Z0 = 50 Ω is terminated by a load
RL = ZL = 100 Ω. Find V.S.W.R, ZMIN and ZMAX
L 0
L
L 0
Z Z
Z Z
−
 =
+
L
100 50 50
100 50 150
−
 = =
+
L 0.33
 =
Arpan Deyasi
Electromagnetic
Theory

30. 24-11-2021 Arpan Deyasi, EM Theory 30
L
L
1
V.S.W.R
1
+ 
=
− 
1
1
3
V.S.W.R
1
1
3
+
=
−
V.S.W.R 2
=
Arpan Deyasi
Electromagnetic
Theory

31. 24-11-2021 Arpan Deyasi, EM Theory 31
L
MAX 0
L
1
Z Z
1
 
+ 
=  
− 
 
L
MIN 0
L
1
Z Z
1
 
− 
=  
+ 
 
MAX
Z 100
= 
MIN
Z 25
= 
Arpan Deyasi
Electromagnetic
Theory

32. 24-11-2021 Arpan Deyasi, EM Theory 32
Problem 5
Soln
A lossless transmission line with a characteristics impedance of 75 Ω is terminated
by a load of impedance 120 Ω. If the magnitude of incident voltage is 10 V. Calculate
the minimum and maximum values of voltages on the line.
L 0
L
L 0
Z Z
Z Z
−
 =
+
L
45
195
 =
L
120 75
120 75
−
 =
+
L 0.243
 =
Arpan Deyasi
Electromagnetic
Theory

33. 24-11-2021 Arpan Deyasi, EM Theory 33
( )
Max 0 L
V V 1
= + 
( )
Min 0 L
V V 1
= − 
( )
Max
V 10 1 0.243
= +
Max
V 12.43V
=
( )
Min
V 10 1 0.243
= −
Min
V 7.57V
=
Arpan Deyasi
Electromagnetic
Theory