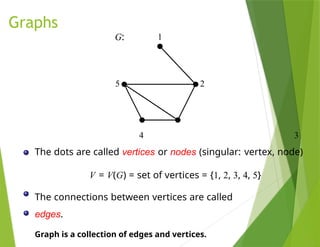
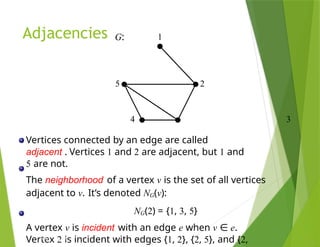
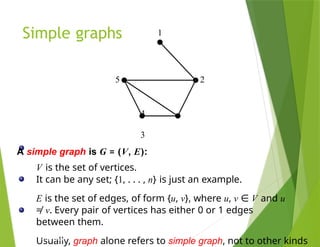
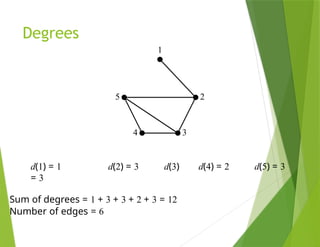
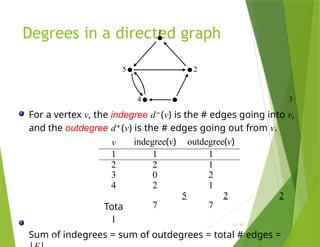
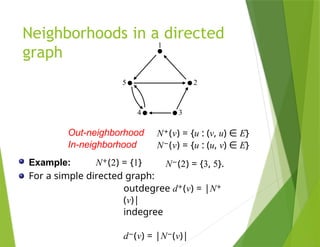
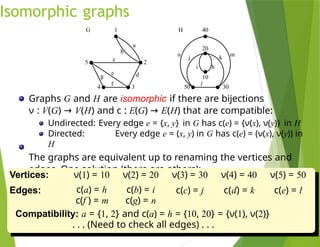
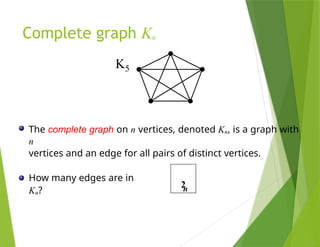
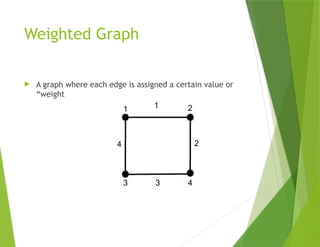
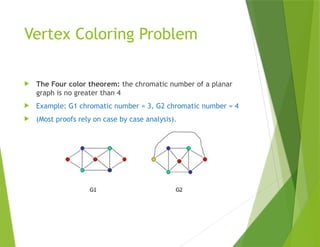
The document provides an overview of graph theory, detailing concepts such as vertices, edges, simple graphs, directed graphs, and various types of special graphs like bipartite, multigraphs, and pseudographs. It also discusses important applications of graph theory in fields such as social networks, computer networks, and transportation systems, along with techniques for analyzing network relationships and dynamics. Key concepts include graph coloring, shortest paths, and centrality measures, which have practical implications in routing, community detection, and information spread.

1. Graph theory
M. GAYATHRI
ASSISTANT PROFESSOR
DEPARTMENT OF MATHEMATICS
SRI SARADA NIKETAN COLLEGE OF SCIENCE FOR WOMEN,KARUR-5

2. Graphs
G:
4 3
The dots are called vertices or nodes (singular: vertex, node)
V = V(G) = set of vertices = {1, 2, 3, 4, 5}
The connections between vertices are called
edges.
Graph is a collection of edges and vertices.
5 2
1
Prof. Tesler

3. Definitions – Edge Type
 Loop: A loop is an edge whose endpoints are equal i.e.,
an edge joining a vertex to it self is called a loop.
Represented as {u, u} = {u}
 Multiple Edges: Two or more edges joining the same
pair of vertices.

4. Adjacencies G:
4 3
Vertices connected by an edge are called
adjacent . Vertices 1 and 2 are adjacent, but 1 and
5 are not.
The neighborhood of a vertex v is the set of all vertices
adjacent to v. It’s denoted NG(v):
NG(2) = {1, 3, 5}
A vertex v is incident with an edge e when v ∈ e.
Vertex 2 is incident with edges {1, 2}, {2, 5}, and {2,
5 2
1
Prof. Tesler

5. Simple graphs
5 2
1
4
3
A simple graph is G = (V, E):
V is the set of vertices.
It can be any set; {1, . . . , n} is just an example.
E is the set of edges, of form {u, v}, where u, v ∈ V and u
≠ v. Every pair of vertices has either 0 or 1 edges
between them.
Usually, graph alone refers to simple graph, not to other kinds
Prof. Tesler

6. Degrees
4
3
The degree of a vertex is the number of edges on
it:
d(1) = 1 d(2) = 3 d(3) = 3 d(4) =
2
5 2
1
d(5) = 3
The degree sequence is to list the degrees in descending
order:
3, 3, 3, 2, 1
The minimum degree is denoted δ(G).
The maximum degree is denoted ∆(G).
δ(G) = 1
∆(G) = 3
Prof. Tesler

7. Degrees
3
5 2
1
4
d(1) = 1 d(2) = 3 d(3)
= 3
Sum of degrees = 1 + 3 + 3 + 2 + 3 = 12
Number of edges = 6
d(4) = 2 d(5) = 3
Prof. Tesler

8. Multigraphs and pseudographs
h
1
2
3
4
a
b
f
c
d
e
g
Some networks have multiple edges between two vertices.
Notation {3, 4} is ambiguous, so write labels on the edges: c,
d, e.
There can be an edge from a vertex to itself, called a loop
(such as h above). A loop has one vertex, so {2, 2} = {2}.
A simple graph does not have multiple edges or loops.
Prof. Tesler

9. Multigraphs and pseudographs
Computer network with multiple connections between
machines.
Transportation network with multiple routes between stations.
But: A graph of Facebook friends is a simple graph. It does not
have multiple edges, since you’re either friends or you’re not.
Also, you cannot be your own Facebook friend, so no loops.
Prof. Tesler

10. Directed graph (a.k.a.
digraph)
5
1
2
3
4
A directed edge (also called an arc) is a connection with
a direction.
One-way transportation routes.
Broadcast and satellite TV / radio are one-way connections
from the broadcaster to your antenna.
Familiy tree: parent → child
Prof. Tesler

11. Directed graph (a.k.a.
digraph)
5
1
2
V = {1, 2, 3, 4, 5}
E = {(1, 5), (2, 1), (3, 2), (3, 4), (4, 5), (5, 2), (5, 4)}
4 3
Represent a directed edge u → v by an ordered pair (u, v).
E.g., 3 → 2 is (3, 2), but we do not have 2 → 3, which is (2,
3).
A directed graph is simple if each (u, v) occurs at most once,
and there are no loops.
Represent it as G = (V, E) or G→ = (V, →E).
V is a set of vertices. It can be any set.
E is the set of edges. Each edge has form (u, v) with u, v ∈ V, u ≠
v. It is permissible to have both (4, 5) and (5, 4), since they are
distinct.
Prof. Tesler

12. Degrees in a directed graph
12 / 42
5
1
2
4 3
For a vertex v, the indegree d−(v) is the # edges going into v,
and the outdegree d+(v) is the # edges going out from v.
v indegree(v) outdegree(v)
1 1 1
2 2 1
3 0 2
4 2 1
Tota
l
7 7
5 2 2
Sum of indegrees = sum of outdegrees = total # edges =
Prof. Tesler

13. Neighborhoods in a directed
graph
5
1
2
3
4
Out-neighborhood
In-neighborhood
Example: N+(2) = {1}
N+(v) = {u : (v, u) ∈ E}
N−(v) = {u : (u, v) ∈ E}
N−(2) = {3, 5}.
For a simple directed graph:
outdegree d+(v) = |N+
(v)|
indegree
d−(v) = |N−(v)|
Prof. Tesler

14. Directed multigraph
1
2
3
4
5
a
d
h
c
e
f
g
i
b 


1
2
3
4
5
1 1 0 0
0 1
2 1 0 0
0 0
A = 3 0 1
0 1 0
4 0 0 0
0 1
5 0 2 0
1 0



V = {1, . . . , 5} φ(a) = (2, 1) φ(d) = (3, 2) φ(g) = (3, 4)
E = {a, . . . , i} φ(b) = (1, 5) φ(e) = (5, 2) φ(h) = (4, 5)
φ(c) = (1, 1) φ(f ) = (5, 2) φ(i) = (5, 4)
A directed multigraph may have loops and multiple edges.
Represent it as G = (V, E, φ).
Name the edges with labels. Let E be the set of the labels.
φ(L) = (u, v) means the edge with label L goes from u to v.
Technicality: A loop counts once in indegree, outdegree, and
avv.Prof. Tesler

15. Isomorphic graphs
Math 154 /
Winter 2020
Ch. 1. Intro to Graph Theory 15 / 42
10
l
5 2
1
20
4 3 50 30
40
a
b
d
c
e
f
g
h
i
k
j
m
n
G H
Graphs G and H are isomorphic if there are bijections
ν : V(G) → V(H) and c : E(G) → E(H) that are compatible:
Undirected: Every edge e = {x, y} in G has c(e) = {ν(x), ν(y)} in H
Directed: Every edge e = (x, y) in G has c(e) = (ν(x), ν(y)) in
H
The graphs are equivalent up to renaming the vertices and
edges. One solution (there are others):
Vertices:
Edges:
ν(3) = 30
c(c) = j
ν(4) = 40
c(d) = k
ν(5) = 50
c(e) = l
ν(1) = 10
c(a) = h
c(f ) = m
ν(2) = 20
c(b) = i
c(g) = n
Compatibility: a = {1, 2} and c(a) = h = {10, 20} = {ν(1), ν(2)}
. . . (Need to check all edges) . . .
Prof. Tesler

16. Unlabeled graphs
In an unlabeled graph, omit the labels on the vertices and
edges.
If labeled graphs are isomorphic, then removing the labels
gives equivalent unlabeled graphs.
This simplifies some problems by reducing the number of
graphs (e.g., 1044 unlabeled simple graphs on 7 vertices vs.
221 labeled).
Prof. Tesler

17. Application: Polyhedra
http://commons.wikimedia.org/wiki/
File:Dodecahedron.svg
A dodecahedron is a 3D shape with 20 vertices, 30 edges, and
12 pentagonal faces.
Unlabeled graphs are used in studying other polyhedra,
polygons and tilings in 2D, and other geometric
configurations. We can treat them as unlabeled, or pick one
labeling if needed.
Prof. Tesler

18. Complete graph Kn
K5
How many edges are in
Kn?
2
The complete graph on n vertices, denoted Kn, is a graph with
n
vertices and an edge for all pairs of distinct vertices.
n
Prof. Tesler

19. Bipartite graph B
A
A bipartite graph is a graph in which:
The set of vertices can be split as V = A ∪ B, where A ∩ B =
∅. Every edge has the form {a, b} where a ∈ A and b ∈ B.
Note that there may be vertices a ∈ A, b ∈ B that do not have
an edge.
Prof. Tesler

20. Subgraphs
 A subgraph of a graph G = (V, E) is a graph H =(V’, E’)
where V’ is a subset of V and E’ is a subset of E
Application example: solving sub-problems within a
graph
Representation example: V = {u, v, w}, E = ({u, v}, {v,
w}, {w, u}}, H1 , H2

21. Subgraphs
 G = G1 U G2 wherein E = E1 U E2 and V = V1 U V2, G,
G1 and G2 are simple graphs of G
Representation example: V1 = {u, w}, E1 = {{u, w}},
V2 = {w, v},
E1 = {{w, v}}, V = {u, v ,w}, E = {{{u, w}, {{w, v}}

22. Weighted Graph
 A graph where each edge is assigned a certain value or
“weight

23. The Seven Bridges of
Königsberg, Germany
 The residents of Königsberg, Germany, wondered if it
was possible to take a walking tour of the town that
crossed each of the seven bridges over the Presel river
exactly once. Is it possible to start at some node and
take a walk that uses each edge exactly once, and ends
at the starting node?

24. The Seven Bridges of
Königsberg, Germany
 You can redraw the original picture as long as for every
edge between nodes i and j in the original you put an
edge between nodes i and j in the redrawn version (and
you put no other edges in the redrawn version).
 Original:
 Redrawn:
4
2 3

25. The Seven Bridges of
Königsberg, Germany
 Euler:
 Has no tour that uses each edge exactly once.
 (Even if we allow the walk to start and finish in
different places.)
 Can you see why?

26. Euler - theorems
1. A connected graph G is Eulerian if and only if G is
connected and has no vertices of odd degree
2. A connected graph G is has an Euler trail from
node a to some other node b if and only if G is connected
and a  b are the only two nodes of odd degree

27. Hamiltonian Graph
 Hamiltonian path (also called traceable path) is a path
that visits each vertex exactly once.
 A Hamiltonian cycle (also called Hamiltonian circuit,
vertex tour or graph cycle) is a cycle that visits each
vertex exactly once (except for the starting vertex, which
is visited once at the start and once again at the end).
 A graph that contains a Hamiltonian path is called a
traceable graph. A graph that contains a Hamiltonian
cycle is called a Hamiltonian graph. Any Hamiltonian
cycle can be converted to a Hamiltonian path by removing
one of its edges, but a Hamiltonian path can be extended
to Hamiltonian cycle only if its endpoints are adjacent.

28. A graph of the vertices of a
dodecahedron.
Is it Hamiltonian?

29. Shortest Path
 Generalize distance to weighted setting
 Digraph G = (V,E) with weight function W: E ® R (assigning
real values to edges)
 Weight of path p = v1 ® v2 ® … ® vk is
 Shortest path = a path of the minimum weight
 Applications
 static/dynamic network routing
 robot motion planning
 map/route generation in traffic
1
1
1
( ) ( , )
k
i i
i
w p w v v





30. Dijkstra's Algorithm
 The Dijkstra Algorithm is used to find the shortest path
from the ‘source node/vertex’ to all the
adjacent/surrounding nodes.
 This method is still currently used by navigational apps,
including Google Maps, Apple Maps, and more.

31. Graph coloring
 Graph coloring is an assignment of "colors", almost always
taken to be consecutive integers starting from 1 without loss
of generality, to certain objects in a graph. Such objects can
be vertices, edges, faces, or a mixture of the above.
 Application examples: scheduling, register allocation in a
microprocessor, frequency assignment in mobile radios, and
pattern matching

32. Vertex Coloring Problem
 Assignment of colors to the vertices of the graph such
that proper coloring takes place (no two adjacent
vertices are assigned the same color)
 Chromatic number: least number of colors needed to
color the graph
 A graph that can be assigned a (proper) k-coloring is k-
colorable, and it is k-chromatic if its chromatic
number is exactly k.

33. Vertex Coloring Problem
 The Four color theorem: the chromatic number of a planar
graph is no greater than 4
 Example: G1 chromatic number = 3, G2 chromatic number = 4
 (Most proofs rely on case by case analysis).

34. Overview of Applications
Graph theory applications include:
 Computer Networks
 Social Networks
 Biology and Chemistry
 Transportation Systems
 Telecommunications

35. Application in Computer
Networks
 Graph theory models communication networks (e.g., the
Internet).
 Nodes represent computers/routers, edges represent
data links.
 Routing algorithms (Dijkstra's, Bellman-Ford) optimize
data transmission

36. Application of graph theory in
social network
 Community Detection: Graph theory helps identify
clusters or communities within a social network where
nodes are more densely connected to each other than
to nodes outside the cluster. Techniques such as
modularity optimization, spectral clustering, and the
Louvain method are used to detect these communities,
which can reveal groups with similar interests or
characteristics.

37. Application of graph theory in
social network
 Centrality Measures: Centrality measures help identify
the most important or influential nodes in a network.
Common centrality measures include:
 Degree Centrality: Measures the number of direct
connections a node has.
 Betweenness Centrality: Measures the extent to which a
node lies on paths between other nodes, indicating its role
in facilitating communication.
 Closeness Centrality: Measures how quickly a node can
reach other nodes in the network, based on shortest paths.
 Eigenvector Centrality: Measures a node’s influence based
on the number and quality of connections it has,
considering the centrality of its neighbors.

38. Application of graph theory in
social network
 Influence and Information Spread: Graph theory
models how information, influence, or behaviors spread
through a network. Models such as the Independent
Cascade Model and the Linear Threshold Model help
understand how innovations, rumors, or diseases
propagate through social networks.
 Network Dynamics and Evolution: Graph theory helps
analyze how social networks change over time. This
includes studying patterns of network growth, changes
in connections, and the formation or dissolution of
communities.

39. Application of graph theory in
social network
 Recommendation Systems: In platforms like social media or e-
commerce, graph-based algorithms are used to recommend
friends, content, or products based on the connections and
behaviors of users. Collaborative filtering and content-based
filtering often utilize graph structures to improve
recommendations.
 Social Network Analysis (SNA): SNA uses graph theory to analyze
social relationships and interactions. It includes studying various
network metrics and visualizations to understand the structure,
dynamics, and behaviors within the network.
 Structural Holes and Brokerage: Graph theory helps identify nodes
that act as bridges or brokers between different parts of a
network. These nodes fill "structural holes" and can be crucial for
information flow and innovation. They often have unique positions
that allow them to control or influence the flow of information
between disparate groups.

40. Application of graph theory in
social network
 Epidemiology and Disease Spread: In the context of public health, graph
theory models help understand and predict the spread of diseases within
social networks. This can inform strategies for controlling outbreaks by
identifying key individuals or groups to target for vaccination or information
dissemination.
 Social Influence and Behavioral Analysis: Graph theory is used to analyze
how social influence affects behavior and decision-making. By modeling
interactions and influence patterns, researchers can study phenomena such
as peer pressure, social contagion, and collective decision-making.
 Fraud Detection and Security: In security and fraud detection, graph theory
helps identify suspicious activities and connections. By analyzing patterns of
transactions or communications, one can detect unusual behavior that may
indicate fraudulent activity or security breaches.
 Overall, graph theory provides a rich set of tools for analyzing and
interpreting the complex and interconnected nature of social networks,
leading to insights that can drive better decision-making, enhance user
experience, and address various challenges in social and organizational
contexts.

41. Application in Biology (Gene
Networks)
 Gene regulatory networks use graph theory to represent
gene interactions.
 Nodes represent genes, and edges show activation or
inhibition relationships.

42. Application in Chemistry
(Molecules)
 Atoms are nodes and bonds are edges in molecular
structures.
 Graph isomorphism identifies molecules with the same
structure.
 Graph theory has several fascinating applications in
chemistry, helping chemists to model and analyze
molecular structures, predict properties, and
understand complex interactions. Here are some
notable applications:

43. Application in Chemistry
 Graph Invariants: These are properties of a graph that remain
unchanged under graph isomorphisms. In chemistry, they help
in identifying isomers and studying molecular symmetry.
 Spectral Graph Theory: This involves studying the properties of
graphs through their eigenvalues. In chemistry, spectral graph
theory is used to analyze molecular orbitals and electronic
properties. The adjacency matrix and Laplacian matrix of the
molecular graph can provide insights into the stability and
reactivity of molecules.
 Chemical Reaction Networks: Graph theory helps in modeling
and analyzing complex chemical reaction networks. Here,
reactions can be represented as edges and species as nodes.
This representation helps in understanding reaction pathways,
network topology, and identifying key intermediates or
catalysts.

44. Application in Chemistry
 Isomerism and Stereochemistry: Graph theory is used to
study isomerism and stereochemistry by analyzing how
different configurations or arrangements of atoms affect
the molecular graph. This helps in understanding
enantiomers, diastereomers, and other stereoisomers.
 Protein and DNA Structure: In biochemistry, graph theory
is applied to model and analyze the structure of proteins
and DNA. For instance, proteins can be represented as
graphs where nodes represent amino acids and edges
represent interactions between them. This helps in
understanding protein folding and function. Similarly,
DNA sequences and their interactions can be studied
using graph theory to analyze patterns and predict
structural features.

45. Application in Chemistry
 Quantitative Structure-Activity Relationship (QSAR): Graph
theory contributes to QSAR modeling by providing methods to
relate molecular structure (represented as graphs) to biological
activity. This helps in drug design and predicting the activity of
new compounds based on their graph-based descriptors.
 Graph-Based Chemical Informatics: Modern cheminformatics
relies heavily on graph-based methods for database searching,
molecular similarity, and virtual screening. Graph-based
algorithms are used to compare and classify compounds,
predict molecular interactions, and discover new drugs.
 Overall, graph theory provides powerful tools for analyzing and
interpreting chemical data, leading to advancements in
molecular design, drug discovery, and the understanding of
complex chemical systems.

46. Conclusion
 Graph theory plays a crucial role in modeling
relationships and solving optimization problems across
various fields.