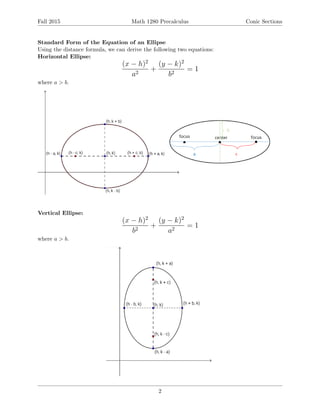
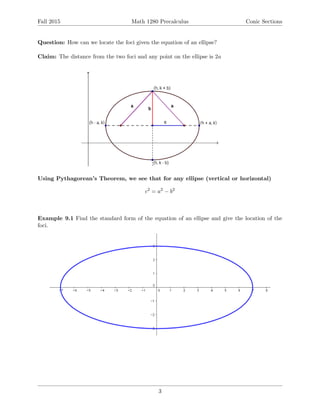
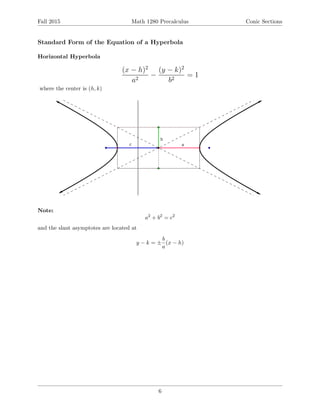
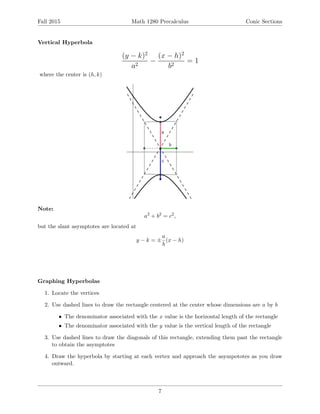
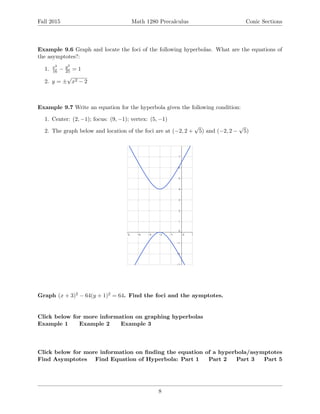
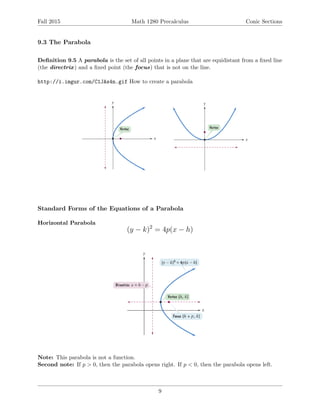
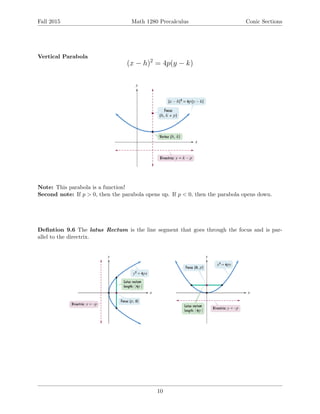
This document provides an overview of conic sections including ellipses, hyperbolas, and parabolas. It defines each conic section geometrically and gives the standard forms of their equations. For each type of conic section, it discusses how to graph them from their equations and how to find their key features like foci, vertices, asymptotes, and directrix. Examples are provided to demonstrate finding equations from given information and graphing various conic sections. The document is intended to teach students about conic sections and analytic geometry.

1. Fall 2015 Math 1280 Precalculus Conic Sections
9 Conic Sections and Analytic Geometry
9.1 The Ellipse
http://i.imgur.com/fOX3z8c.gif How to create an ellipse
Definition 9.1 An ellipse is the set of all points P in a plane such that the sum of the dis-
tances to the two focal points is constant. These two focal points are called foci. The midpoint
between the two foci is called the center.
Definition 9.2 The line through the foci intersects the ellipse at the vertices. The major axis
is the line segment that joins vertices while the minor axis is the line segment perpendicular to
the major axis that intersects the center.
https://en.wikipedia.org/wiki/File:Ellipse_Animation.gif How to create an ellipse
1

2. Fall 2015 Math 1280 Precalculus Conic Sections
Standard Form of the Equation of an Ellipse
Using the distance formula, we can derive the following two equations:
Horizontal Ellipse:
(x − h)2
a2
+
(y − k)2
b2
= 1
where a > b.
Vertical Ellipse:
(x − h)2
b2
+
(y − k)2
a2
= 1
where a > b.
2

3. Fall 2015 Math 1280 Precalculus Conic Sections
Question: How can we locate the foci given the equation of an ellipse?
Claim: The distance from the two foci and any point on the ellipse is 2a
Using Pythagorean’s Theorem, we see that for any ellipse (vertical or horizontal)
c2
= a2
− b2
Example 9.1 Find the standard form of the equation of an ellipse and give the location of the
foci.
3

4. Fall 2015 Math 1280 Precalculus Conic Sections
Example 9.2 Find the standard form of the equation of an ellipse and give the location of the foci.
Example 9.3 Find the standard form of the equation of an ellipse satisfying the following: foci at
(−6, 0) and (6, 0); vertices at (−10, 0) and (10, 0)
Example 9.4 Graph 25(x + 4)2 + 4(y + 2)2 = 100 and find the foci.
Example 9.5 A semi elliptical archway over a one-way road has a height of 10 feet and a width of
40 feet. Your truck has a width of 10 feet and a height of 9 feet. Will your truck clear the opening
of the archway?
Click below for more information on graphing ellipses
Example 1 Example 2 Example 3 Example 4 Example 5
Click below for more information on determining the equation on an ellipse from
given information
Example 1 Example 2 Example 3
4

5. Fall 2015 Math 1280 Precalculus Conic Sections
9.2 The Hyperbola
Definition 9.3 A hyperbola is the set of point in a plane, the difference of the distances to the
foci is constant.
Defintion 9.4 The line segments that joins the vertices is the transverse axis
5

6. Fall 2015 Math 1280 Precalculus Conic Sections
Standard Form of the Equation of a Hyperbola
Horizontal Hyperbola
(x − h)2
a2
−
(y − k)2
b2
= 1
where the center is (h, k)
Note:
a2
+ b2
= c2
and the slant asymptotes are located at
y − k = ±
b
a
(x − h)
6

7. Fall 2015 Math 1280 Precalculus Conic Sections
Vertical Hyperbola
(y − k)2
a2
−
(x − h)2
b2
= 1
where the center is (h, k)
Note:
a2
+ b2
= c2
,
but the slant asymptotes are located at
y − k = ±
a
b
(x − h)
Graphing Hyperbolas
1. Locate the vertices
2. Use dashed lines to draw the rectangle centered at the center whose dimensions are a by b
• The denominator associated with the x value is the horizontal length of the rectangle
• The denominator associated with the y value is the vertical length of the rectangle
3. Use dashed lines to draw the diagonals of this rectangle, extending them past the rectangle
to obtain the asymptotes
4. Draw the hyperbola by starting at each vertex and approach the asympototes as you draw
outward.
7

8. Fall 2015 Math 1280 Precalculus Conic Sections
Example 9.6 Graph and locate the foci of the following hyperbolas. What are the equations of
the asymptotes?:
1. x2
16 − y2
25 = 1
2. y = ±
√
x2 − 2
Example 9.7 Write an equation for the hyperbola given the following condition:
1. Center: (2, −1); focus: (9, −1); vertex: (5, −1)
2. The graph below and location of the foci are at (−2, 2 +
√
5) and (−2, 2 −
√
5)
Graph (x + 3)2 − 64(y + 1)2 = 64. Find the foci and the aymptotes.
Click below for more information on graphing hyperbolas
Example 1 Example 2 Example 3
Click below for more information on finding the equation of a hyperbola/asymptotes
Find Asymptotes Find Equation of Hyperbola: Part 1 Part 2 Part 3 Part 5
8

9. Fall 2015 Math 1280 Precalculus Conic Sections
9.3 The Parabola
Definition 9.5 A parabola is the set of all points in a plane that are equidistant from a fixed line
(the directrix) and a fixed point (the focus) that is not on the line.
http://i.imgur.com/C1JAs4n.gif How to create a parabola
Standard Forms of the Equations of a Parabola
Horizontal Parabola
(y − k)2
= 4p(x − h)
Note: This parabola is not a function.
Second note: If p > 0, then the parabola opens right. If p < 0, then the parabola opens left.
9

10. Fall 2015 Math 1280 Precalculus Conic Sections
Vertical Parabola
(x − h)2
= 4p(y − k)
Note: This parabola is a function!
Second note: If p > 0, then the parabola opens up. If p < 0, then the parabola opens down.
Defintion 9.6 The latus Rectum is the line segment that goes through the focus and is par-
allel to the directrix.
10

11. Fall 2015 Math 1280 Precalculus Conic Sections
Graphing Parabolas
1. Write the equation in standard form.
2. From the equation, determine whether the parabola is horizontal or vertical, and the location
of the vertex.
3. Plot the vertex.
4. Determine p, noting whether p is positive or negative, in order to find the directrix and focus.
5. Plot the focus and use a dotted line to indicate the directrix.
6. Plot two additional points. For a horizontal parabola, plug in the point x = h + p. For a
vertical parabola, plug in the point y = k + p.
These points will be at the intersection of the latus rectum and the parabola.
7. Draw the parabola by connecting the vertex to the two additional points and drawing outward.
Example 9.8 Graph the following parabola and find the focus and directrix:
1. 8y2 + 3x = 0
2. (x − 2)2 = −8(y + 4)
Find the equation of the parabola given the following:
1. Focus: (15, 0); directrix: x = −15
2. Vertex: (5, −2); focus: (5, −3)
Click here for more information on graphing parabolas
Click here for information on finding the directrix and focus of a parabola given the
equation
Click below for more information on finding the equation of a parabola
Example 1 Example 2 Example 3
11