1) Surveyors use vectors to create scaled maps, representing magnitudes and directions. Vectors are described using polar coordinates (R,θ) where R is magnitude and θ is the angle measured from the x-axis. 2) Polar coordinates can be converted to rectangular coordinates (x,y) using trigonometry. The x-component is Rcosθ and y-component is Rsinθ. 3) The resultant of adding vectors can be found graphically by drawing the vectors to scale and measuring the angle and length of the summed vector, or analytically by using trigonometry functions.

1. Vectors

2. Surveyors use accurate measures of magnitudes and directions to create scaled maps of large regions. Vectors

3. Identifying Direction N 50o 60o E W 60o 60o S A common way of identifying direction is by reference to East, North, West, and South. (Locate points below.) Length = 40 m 40 m, 50o N of E 40 m, 60o N of W 40 m, 60o W of S 40 m, 60o S of E

4. Identifying Direction N 45o N E W E W 50o S S Write the angles shown below by using references to east, south, west, north. 500 S of E 450 W of N

5. 90o 90o R q 50o 180o 180o 0o 0o 270o 270o Vectors and Polar Coordinates Polar coordinates (R,q) are an excellent way to express vectors. Consider the vector 40 m, 500 N of E, for example. 40 m R is the magnitude and q is the direction.

6. 90o 0o 180o 50o 60o 60o 60o 3000 210o 270o 120o Vectors and Polar Coordinates Polar coordinates (R,q) are given for each of four possible quadrants: = 40 m, 50o = 40 m, 120o = 40 m, 210o = 40 m, 300o

7. y (-2, +3) (+3, +2) + + x - Right, up = (+,+) Left, down = (-,-) (x,y) = (?, ?) - (+4, -3) (-1, -3) Rectangular Coordinates Reference is made to x and y axes, with + and -numbers to indicate position in space.

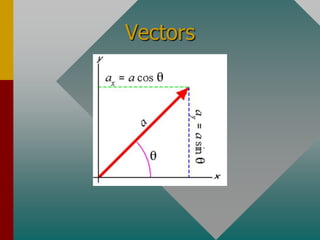
8. R y q x Trigonometry Review Application of Trigonometry to Vectors Trigonometry y = R sin q x = R cos q R2 = x2 + y2

9. q Finding Components of Vectors A component is the effect of a vector along other directions. The x and y components of the vector are illustrated below. = A cosq = A sin q Finding components: Polar to Rectangular Conversions

10. Example 2:A person walks 400.0 m in a direction of 30.0oSof W (210o). How far is the displacement westand how far south? 30o 400 m The x-component (W) is adjacent: = -A cosq The y-component (S) is opposite: = -A sinq

11. Vector Addition Resultant ( ) - sum of two or more vectors. Vector Resolutions: 01. GRAPHICAL SOLUTION – use ruler and protractor to draw and measure the scaled magnitude and angle (direction), respectively. 02. ANALYTICAL SOLUTION - use trigonometry

12. q Example 11:A bike travels 20 m, E then 40 m at 60o N of W, and finally 30 m at 210o. What is the resultant displacement graphically? Graphically, we use ruler and protractor to draw components, then measure the Resultant R,q C = 30 m B = 40 m 30o R 60o f A = 20 m, E R = (32.6 m, 143.0o) Let 1 cm = 10 m

13. Cy 30o R Ry 60o f 0 q Ax Rx Bx Cx A Graphical Understanding of the Components and of the Resultant is given below: Note: Rx = Ax + Bx + Cx By B Ry = Ay + By + Cy C A

14. Resultant of Perpendicular Vectors Finding resultant of two perpendicular vectors is like changing from rectangular to polar coord. R y q x R is always positive; q is from + x axis

15. First Consider A + B Graphically: B B R B A A Vector Difference For vectors, signs are indicators of direction. Thus, when a vector is subtracted, the sign (direction) must be changed before adding. R = A + B

16. Now A – B: First change sign (direction) of B, then add the negative vector. B B -B A R’ -B A A Vector Difference For vectors, signs are indicators of direction. Thus, when a vector is subtracted, the sign (direction) must be changed before adding.

17. Subtraction results in a significant difference both in the magnitude and the direction of the resultant vector. |(A – B)| = |A| - |B| Comparison of addition and subtraction of B B B A R R’ -B B A A Addition and Subtraction R = A + B R’ = A - B

18. A – B; B - A +A -A +B -B A 2.43 N B 7.74 N Example 13.Given A = 2.4 km, N and B = 7.8 km, N: find A – B and B – A. A - B B - A R R (2.43 N – 7.74 S) (7.74 N – 2.43 S) 5.31 km, S 5.31 km, N