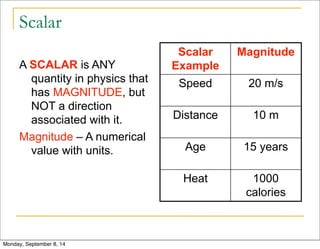
This document discusses vectors and scalars in physics. It defines a scalar as a quantity that has magnitude but no direction, while a vector has both magnitude and direction. Vectors are represented by arrows to show both magnitude and direction. The document provides examples of applying vectors to problems involving addition, subtraction, and resolving perpendicular components using trigonometry. It demonstrates solving vector problems for displacement, velocity, and other physical quantities.