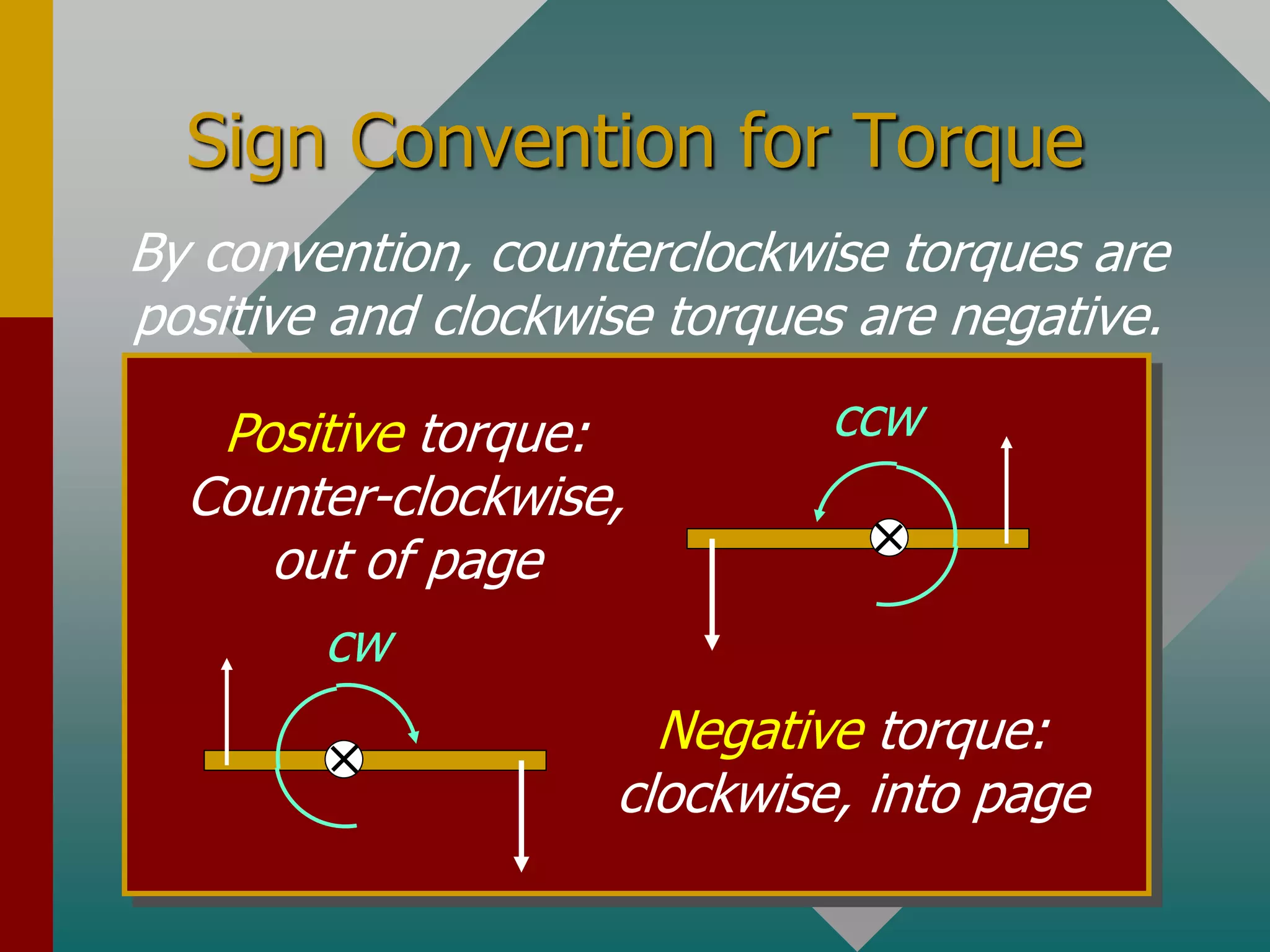
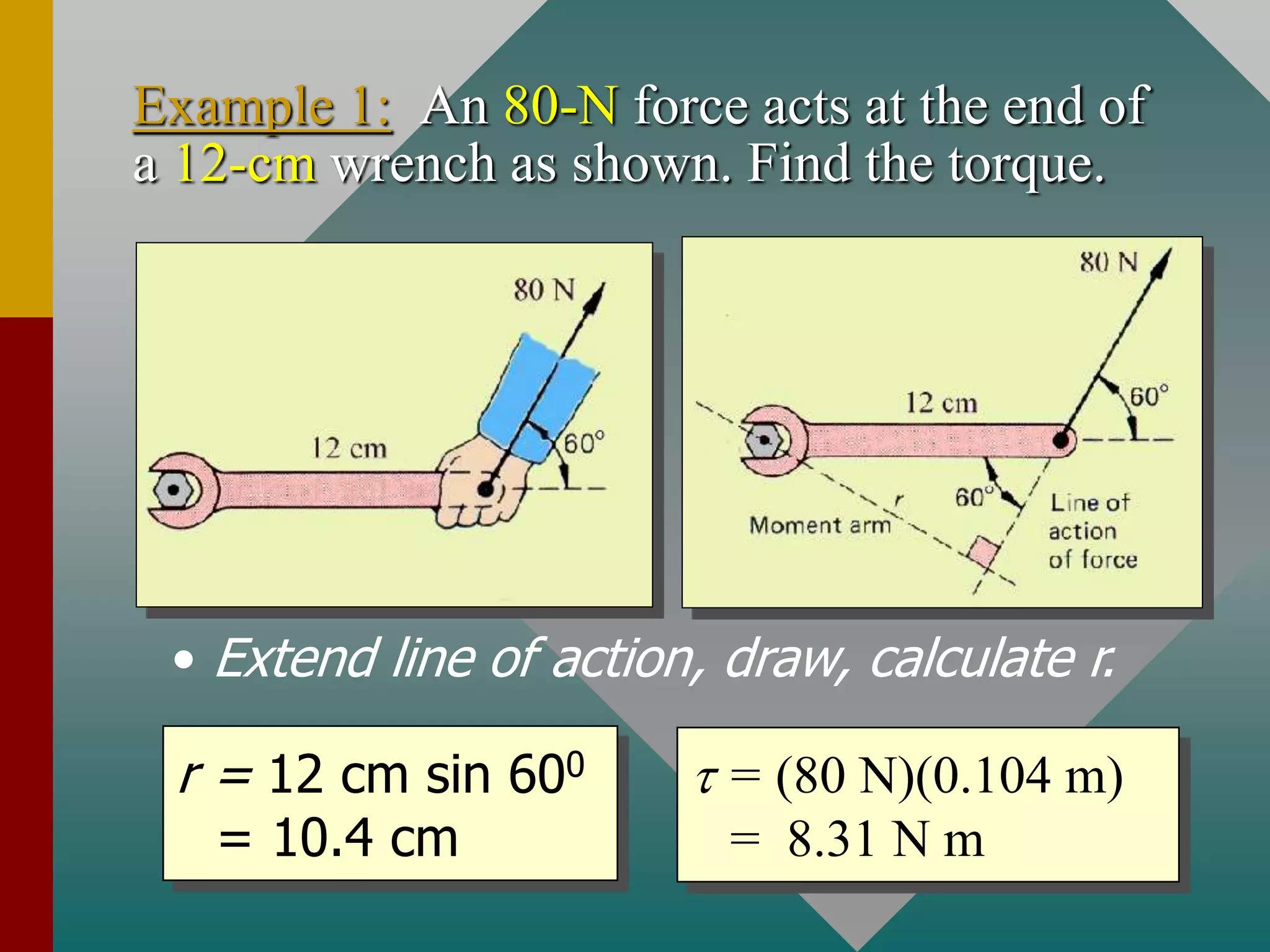
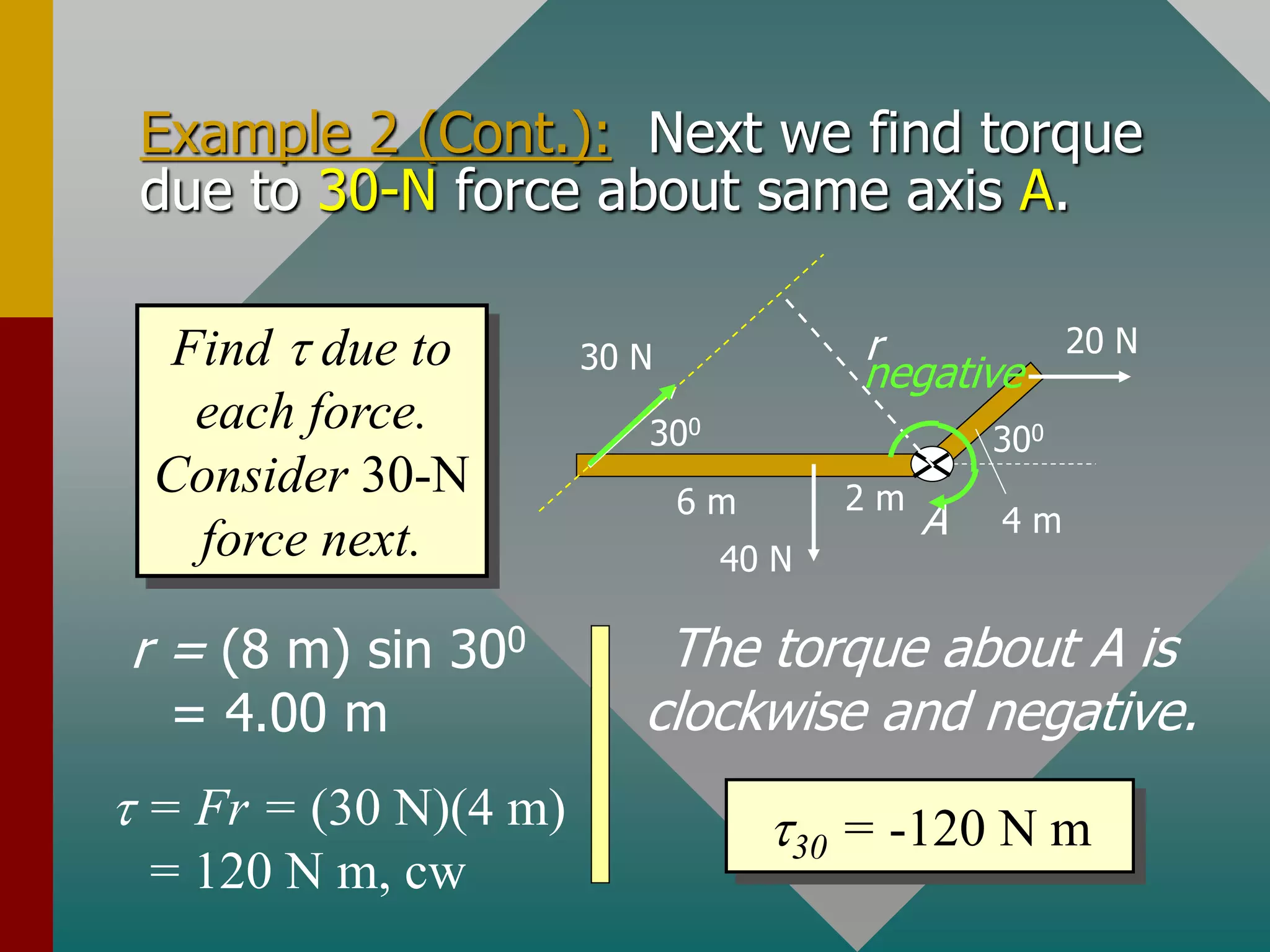
Torque is a measure of the tendency to cause rotation and is determined by three factors: the magnitude of an applied force, the direction of the force, and the location where the force is applied. Torque is calculated as the product of the force and the perpendicular distance from the axis of rotation, known as the moment arm. Newton's second law of motion can be applied to rotational systems by considering torque as the rotational analogue of force and angular acceleration as the rotational analogue of linear acceleration. The rotational inertia, which depends on the mass and how it is distributed relative to the axis of rotation, determines how difficult it is to change an object's rotational motion and is analogous to linear mass.

1. Torque and Equilibrium

2. Torque is a twist
or turn that tends
to produce
rotation. * * *
Applications are
found in many
common tools
around the home
or industry where
it is necessary to
turn, tighten or
loosen devices.

3. Definition of Torque
Torque is defined as the tendency to
produce a change in rotational motion.
Examples:

4. Torque is Determined by Three Factors:
• The magnitude of the applied force.
• The direction of the applied force.
• The location of the applied force.
20 N
Magnitude of force
40 N
The 40-N force
produces twice the
torque as does the
20-N force.
Each of the 20-N
forces has a different
torque due to the
direction of force. 20 N
Direction of Force
20 N
q
q
20 N
20 N
Location of force
The forces nearer the
end of the wrench
have greater torques.
20 N
20 N

5. Units for Torque
Torque is proportional to the magnitude of
F and to the distance r from the axis. Thus,
a tentative formula might be:
t = Fr Sin θ Units: Nm
6 cm
40 N
t = (40 N)(0.60 m)
= 24.0 Nm, cw
t = 24.0 Nm, cw

6. Direction of Torque
Torque is a vector quantity that has
direction as well as magnitude.
Turning the handle of a
screwdriver clockwise and
then counterclockwise will
advance the screw first
inward and then outward.

7. Sign Convention for Torque
By convention, counterclockwise torques are
positive and clockwise torques are negative.
Positive torque:
Counter-clockwise,
out of page
cw
ccw
Negative torque:
clockwise, into page

8. Example 1: An 80-N force acts at the end of
a 12-cm wrench as shown. Find the torque.
• Extend line of action, draw, calculate r.
t = (80 N)(0.104 m)
= 8.31 N m
r = 12 cm sin 600
= 10.4 cm

9. Calculating Resultant Torque
• Read, draw, and label a rough figure.
• Draw free-body diagram showing all forces,
distances, and axis of rotation.
• Extend lines of action for each force.
• Calculate moment arms if necessary.
• Calculate torques due to EACH individual force
affixing proper sign. CCW (+) and CW (-).
• Resultant torque is sum of individual torques.

10. Example 2: Find resultant torque about
axis A for the arrangement shown below:
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Find t due to
each force.
Consider 20-N
force first:
r = (4 m) sin 300
= 2.00 m
t = Fr = (20 N)(2 m)
= 40 N m, cw
The torque about A is
clockwise and negative.
t20 = -40 N m
r
negative

11. Example 2 (Cont.): Next we find torque
due to 30-N force about same axis A.
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Find t due to
each force.
Consider 30-N
force next.
r = (8 m) sin 300
= 4.00 m
t = Fr = (30 N)(4 m)
= 120 N m, cw
The torque about A is
clockwise and negative.
t30 = -120 N m
r
negative

12. Example 2 (Cont.): Finally, we consider
the torque due to the 40-N force.
Find t due to
each force.
Consider 40-N
force next:
r = (2 m) sin 900
= 2.00 m
t = Fr = (40 N)(2 m)
= 80 N m, ccw
The torque about A is
CCW and positive.
t40 = +80 N m
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
r
positive

13. Example 2 (Conclusion): Find resultant
torque about axis A for the arrangement
shown below:
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Resultant torque
is the sum of
individual torques.
tR = - 80 N m Clockwise
tR = t20 + t20 + t20 = -40 N m -120 N m + 80 N m

14. Summary: Resultant Torque
• Read, draw, and label a rough figure.
• Draw free-body diagram showing all forces,
distances, and axis of rotation.
• Extend lines of action for each force.
• Calculate moment arms if necessary.
• Calculate torques due to EACH individual force
affixing proper sign. CCW (+) and CW (-).
• Resultant torque is sum of individual torques.

15. Newtons 2nd law and rotation
• Define and calculate the moment of inertia for
simple systems.
• Define and apply the concepts of Newton’s
second law.

16. Inertia of Rotation
Consider Newton’s second law for the inertia of
rotation to be patterned after the law for translation.
F = 20 N
a = 4 m/s2
Linear Inertia, m
m = = 5 kg
20 N
4 m/s2
F = 20 N
R = 0.5 m
a = 2
rad/s2
Rotational Inertia, I
I = = = 2.5 kg m2
(20 N)(0.5 m)
4 m/s2
t
a
Force does for translation what torque does for rotation:

17. Rotational Inertia
m2
m3
m
4
m
m1
axis
w
v = wR
Object rotating at constant w.
Rotational Inertia is
how difficult it is to
spin an object. It
depends on the mass
of the object and how
far away the object if
from the axis of
rotation (pivot point). Rotational Inertia Defined:
I = SmR2

18. Common Rotational Inertias
2
1
3
I mL
 2
1
12
I mL

L L
R R R
I = mR2 I = ½mR2 2
2
5
I mR

Hoop Disk or cylinder Solid sphere

19. Example 1: A circular hoop and a disk
each have a mass of 3 kg and a radius
of 20 cm. Compare their rotational
inertias.
R
I = mR2
Hoop
R
I = ½mR2
Disk
2 2
(3 kg)(0.2 m)
I mR
 
2 2
1 1
2 2 (3 kg)(0.2 m)
I mR
 
I = 0.120 kg m2
I = 0.0600 kg m2

20. Newton 2nd Law
For many problems involving rotation, there is an
analogy to be drawn from linear motion.
x
f
R
4 kg
w
t
wo  50 rad/s
t = 40 N m
A resultant force F
produces negative
acceleration a for a
mass m.
F ma

I
m
A resultant torque t
produces angular
acceleration a of disk
with rotational inertia I.
I
t a


21. Newton’s 2nd Law for Rotation
R
4 kg
w
F wo  50 rad/s
R = 0.20 m
F = 40 N
t = Ia
How many revolutions
required to stop?
FR = (½mR2)a
2 2(40N)
(4 kg)(0.2 m)
F
mR
a  
a = 100 rad/s2
2aq  wf
2 - wo
2
0
2 2
0
2
(50 rad/s)
2 2(100 rad/s )
w
q
a
 
 
q = 12.5 rad = 1.99 rev

22. Summary – Rotational Analogies
Quantity Linear Rotational
Displacement Displacement x Radians q
Inertia Mass (kg) I (kgm2)
Force Newtons N Torque N·m
Velocity v “ m/s ” w Rad/s
Acceleration a “ m/s2 ” a Rad/s2

23. CONCLUSION: Chapter 5A
Torque