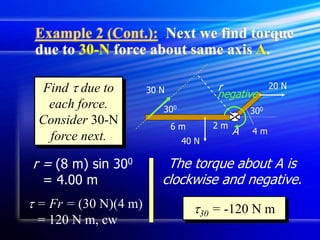
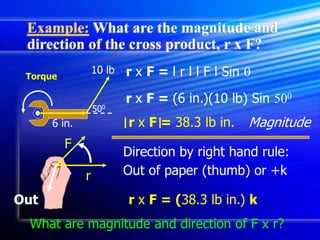
Torque is a twist or rotation produced by a force. It is calculated by multiplying the force by the perpendicular distance (moment arm) from the line of action of the force to the axis of rotation. Torque can be found using the cross product of the force and position vectors. The direction of the torque is given by the right-hand rule. The resultant torque is calculated by finding the individual torques of each force and taking their sum, with clockwise torques having a negative sign and counterclockwise torques having a positive sign.

1. Torque is a twist or
turn that tends to
produce rotation. * *
* Applications are
found in many
common tools around
the home or industry
where it is necessary
to turn, tighten or
loosen devices.
Understanding Torque

2. Definition of Torque
Torque is defined as the tendency to
produce a change in rotational motion.
Examples:

3. Torque is Determined by Three
Factors:
l The magnitude of the applied force.
l The direction of the applied force.
l The location of the applied force.
20 N
Magnitude of force
40 N
The 40-N force
produces twice the
torque as does the
20-N force.
Each of the 20-N
forces has a different
torque due to the
direction of force. 20 N
Direction of Force
20 N
q
q
20 N
20 N
Location of force
The forces nearer the
end of the wrench
have greater torques.
20 N
20 N

4. Units for Torque
Torque is proportional to the magnitude of
F and to the distance r from the axis. Thus,
a tentative formula might be:
t = Fr Units: Nm or lbft
6 cm
40 N
t = (40 N)(0.60 m)
= 24.0 Nm, cw
t = 24.0 Nm, cw

5. Direction of Torque
Torque is a vector quantity that has
direction as well as magnitude.
Turning the handle of a
screwdriver clockwise and
then counterclockwise will
advance the screw first
inward and then outward.

6. Sign Convention for Torque
By convention, counterclockwise torques are
positive and clockwise torques are negative.
Positive torque:
Counter-clockwise,
out of page
cw
ccw
Negative torque:
clockwise, into page

7. Line of Action of a Force
The line of action of a force is an imaginary
line of indefinite length drawn along the
direction of the force.
F1
F2
F3
Line of
action

8. The Moment Arm
The moment arm of a force is the perpendicular
distance from the line of action of a force to the
axis of rotation.
F2
F1
F3
r
r
r

9. Calculating Torque
l Read problem and draw a rough
figure.
l Extend line of action of the force.
l Draw and label moment arm.
l Calculate the moment arm if
necessary.
l Apply definition of torque:
t = Fr Torque = force x moment arm

10. Example 1: An 80-N force acts at the
end of a 12-cm wrench as shown. Find
the torque.
• Extend line of action, draw, calculate r.
t = (80 N)(0.104 m)
= 8.31 N m
r = 12 cm sin 600
= 10.4 cm

11. Alternate: An 80-N force acts at the
end of a 12-cm wrench as shown. Find
the torque.
Resolve 80-N force into components as shown.
Note from figure: rx = 0 and ry = 12 cm
t = (69.3 N)(0.12 m) t = 8.31 N m as before
positive
12 cm

12. Calculating Resultant Torque
• Read, draw, and label a rough figure.
• Draw free-body diagram showing all forces,
distances, and axis of rotation.
• Extend lines of action for each force.
• Calculate moment arms if necessary.
• Calculate torques due to EACH individual force
affixing proper sign. CCW (+) and CW (-).
• Resultant torque is sum of individual torques.

13. Example 2: Find resultant torque about
axis A for the arrangement shown
below:
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Find t due to
each force.
Consider 20-N
force first:
r = (4 m) sin 300
= 2.00 m
t = Fr = (20 N)(2 m)
= 40 N m, cw
The torque about A is
clockwise and negative.
t20 = -40 N m
r
negative

14. Example 2 (Cont.): Next we find torque
due to 30-N force about same axis A.
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Find t due to
each force.
Consider 30-N
force next.
r = (8 m) sin 300
= 4.00 m
t = Fr = (30 N)(4 m)
= 120 N m, cw
The torque about A is
clockwise and negative.
t30 = -120 N m
r
negative

15. Example 2 (Cont.): Finally, we consider
the torque due to the 40-N force.
Find t due to
each force.
Consider 40-N
force next:
r = (2 m) sin 900
= 2.00 m
t = Fr = (40 N)(2 m)
= 80 N m, ccw
The torque about A is
CCW and positive.
t40 = +80 N m
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
r
positive

16. Example 2 (Conclusion): Find resultant
torque about axis A for the arrangement
shown below:
300
300
6 m 2 m
4 m
20 N
30 N
40 N
A
Resultant torque
is the sum of
individual torques.
tR = - 80 N m Clockwise
tR = t20 + t20 + t20 = -40 N m -120 N m + 80 N m

17. Part II: Torque and the Cross
Product or Vector Product.
Optional Discussion
This concludes the general treatment
of torque. Part II details the use of
the vector product in calculating
resultant torque. Check with your
instructor before studying this section.

18. The Vector Product
Torque can also be found by using the vector
product of force F and position vector r. For
example, consider the figure below.
F
q
r
F Sin q
The effect of the force
F at angle q (torque)
is to advance the bolt
out of the page.
Torque
Magnitude:
(F Sin q)r
Direction = Out of page (+).

19. Definition of a Vector
Product
The magnitude of the vector (cross) product
of two vectors A and B is defined as follows:
A x B = l A l l B l Sin q
F x r = l F l l r l Sin q Magnitude only
F
(F Sin q) r or F (r Sin q)
In our example, the cross product of F and r is:
In effect, this becomes simply:
q
r
F Sin q

20. Example: Find the magnitude of the
cross product of the vectors r and F
drawn below:
r x F = l r l l F l Sin q
r x F = (6 in.)(12 lb) Sin 600
r x F = l r l l F l Sin q
r x F = (6 in.)(12 lb) Sin 1200
Explain difference. Also, what about F x r?
12 lb
r x F = 62.4 lb in.
Torque
600
6 in.
Torque
600
6 in.
12 lb r x F = 62.4 lb in.

21. Direction of the Vector
Product.
The direction of a
vector product is
determined by the
right hand rule.
A
C
B
B
-C
A
A x B = C (up)
B x A = -C (Down)
Curl fingers of right hand
in direction of cross pro-
duct (A to B) or (B to A).
Thumb will point in the
direction of product C.
What is direction
of A x C?

22. Example: What are the magnitude and
direction of the cross product, r x F?
r x F = l r l l F l Sin q
r x F = (6 in.)(10 lb) Sin 500
r x F = 38.3 lb in.
10 lb
Torque
500
6 in. Magnitude
Out
r
F
Direction by right hand rule:
Out of paper (thumb) or +k
r x F = (38.3 lb in.) k
What are magnitude and direction of F x r?

23. Summary
Torque is the product of a force and its
moment arm as defined below:
The moment arm of a force is the perpendicular distance
from the line of action of a force to the axis of rotation.
The line of action of a force is an imaginary line of
indefinite length drawn along the direction of the force.
t = Fr Torque = force x moment arm

24. Summary: Resultant Torque
• Read, draw, and label a rough figure.
• Draw free-body diagram showing all forces,
distances, and axis of rotation.
• Extend lines of action for each force.
• Calculate moment arms if necessary.
• Calculate torques due to EACH individual force
affixing proper sign. CCW (+) and CW (-).
• Resultant torque is sum of individual torques.