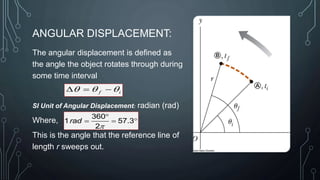
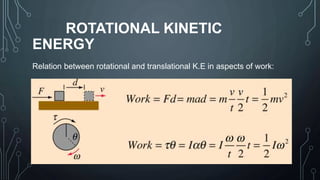
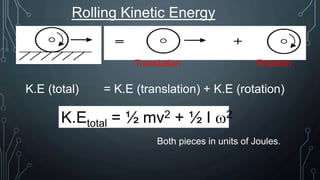
This document discusses key concepts related to rotation, including: - Group members studying rotation include Maimoona, Beenish, Fatima, Sana, Maria, and Irum. - Topics covered are angular position, displacement, velocity, acceleration, centripetal/centrifugal force, torque, rotational kinetic energy, and Newton's second law of rotation. - Newton's second law of rotation states that angular acceleration is proportional to net torque and inversely proportional to moment of inertia.

2. ROTATION

3. Group members:
Maimoona siddiqua
Beenish rubab
Fatima zain
Sana bibi
Maria khalid
Irum sultana

4. Contents:
• Rotation
• Angular position and radian
• Angular displacement
• Angular velocity
• Angular acceleration
• Centripetal and centrifugal force
• Torque
• Rotational kinetic energy
• Newton second law of rotation

5. DEFINITION OF ROTATION
• Rotation is when an object turn about
an axis. OR
• A rotation is a circular movement of an
object around a center (or point) of
rotation. A three-dimensional object
can always be rotated around an
infinite number of imaginary lines
called rotation axes. If the axis passes
through the body's center of mass, the
body is said to rotate upon itself, or
spin.

6. ANGULAR POSITION
The orientation of a body or figure with
respect to a specified reference position as
expressed by the amount of rotation necessary to
change from one orientation to the other about a
specified axis.
The angular position, conventionally
denoted by q. This is the angle at a particular
instant in time that the object makes with respect to
some fixed reference axis.
The arc length and r are related:
s= q r

7. ANGULAR DISPLACEMENT:
The angular displacement is defined as
the angle the object rotates through during
some time interval
SI Unit of Angular Displacement: radian (rad)
Where,
This is the angle that the reference line of
length r sweeps out.
f i
q q q
  
360
1 57.3
2
rad


  

8. DEFINITION OF AVERAGE ANGULAR
VELOCITY:

9. AVERAGE ANGULAR ACCELERATION
The average angular acceleration a, of an object is defined as
the ratio of the change in the angular velocity to the time it takes
for the object to undergo the change.
SI Unit of Angular acceleration: radian per second per second
(rad/s2)
f i
avg
f i
t t t
  
a
 
 
 

10. EXAMPLE:
A JET REVVING ITS ENGINES
• As seen from the front of the engine, the
fan blades are rotating with an angular
speed of
-110 rad/s. As the plane takes off, the
angular velocity of the blades reaches -330
rad/s in a time of 14s.
• Find the angular acceleration, assuming it
to be constant.
solution: f i
avg
f i
t t t
  
a
 
 
 

11. Centripetal force :
• CENTRIPETAL FORCE is a force which acts on a body moving in a
circular path and is directed towards the center around which the body
is moving.
OR
Centripetal force is defined as the
radial force directed towards the
center acting on a body in circular
motion.

12. Nature of centripetal force:
• Magnitude of centripetal force
remains constant.
• Always it acts along the radius.
• It is always directed towards the center.
• Hence, centripetal force is a radial force of
constant magnitude.
• The centripetal force –f acting on a body of mass
-m moving in a circular path is given by
f = mv2/r

13. Centripetal Force and Mass:
• Centripetal force is directly
proportional to the mass of the body.
f α m

14. Centripetal Force and Radius:
• Centripetal force is inversely proportional
to the radius of the body.
f α 1/r

15. Centripetal Force and speed:
•Centripetal force is directly proportional
to square of the velocity of the body.
f α v2

17. EXAMPLES OF CENTRIPETAL FORCE:
For a car travelling around a
circular road with uniform speed,
the centripetal force is provided
by the force of static friction
between tyres of the car
and the road.

18. CENTRIFUGAL FORCE
1. Centrifugal force is an imaginary force experienced only in non-inertial
frames of reference.
2. This force is necessary in order to explain Newton’s laws of motion in an
accelerated frame of reference.
3. Centrifugal force is acts along the radius but is directed away from the
center of the circle.
4. Direction of centrifugal force is always opposite to that of the centripetal
force.
5. Centrifugal force f = mv2/r
6. Centrifugal force is always present in rotating bodies.

19. EXAMPLES OF CENTRIFUGAL FORCE:
1. When a car in motion takes a sudden turn towards left, passengers in
the car experience an outward push to the right. This is due to the
centrifugal force acting on the passengers.
2. The children sitting in a merry-go-round experience an outward force
as the merry-go-round rotates about the vertical axis.

20. August 14, 2023
TORQUE:
• Torque, t, is the tendency of a force to
• rotate an object about some axis
• Let F be a force acting on an object, and let r be a position
vector from a rotational center to the point of application of the
force, with F perpendicular to r. The magnitude of the torque is
given by
rF

t

21. August 14, 2023
TORQUE UNITS AND DIRECTION
• The SI units of torque are N.m
• Torque is a vector quantity
• Torque magnitude is given by
• Torque will have direction
• If the turning tendency of the force is counterclockwise, the torque will be
positive
• If the turning tendency is clockwise, the torque will be negative
Fd
rF 
 q
t sin

22. August 14, 2023
NET TORQUE
• The force will tend to cause a
counterclockwise rotation about O
• The force will tend to cause
clockwise rotation about O
• St  t1 + t2  F1d1 – F2d2
• If St  0, starts rotating
• If St  0, rotation rate does not
change
1
F
2
F
 Rate of rotation of an object does not change,
unless the object is acted on by a net torque

23. NET FORCE = 0 , NET TORQUE ≠ 0
10 N
10 N
• > The net force = 0, since the forces are applied in
opposite directions so it will not accelerate.
• > However, together these forces will make the rod
rotate in the clockwise direction.

24. NET TORQUE = 0, NET FORCE ≠ 0
The rod will accelerate upward under these
two forces, but will not rotate.

25. ANGULAR MOMENTUM
• The quantity of rotation of a body, which is the product of its
moment of inertia and its angular velocity.
• In physics, angular momentum is the rotational equivalent of
linear momentum.

26. RELATION BETWEEN LINEAR
AND ANGULAR MOMENTUM
• The magnitude of angular momentum l is equal to the
product of the magnitude of vector r and magnitude of vector
p and sine of the angle between r and p.
l = r × p.

27. ROTATIONAL KINETIC
ENERGY
DEFINITION:
The energy due to spinning of a body about an axis
is called rotational kinetic energy.

28. ROTATIONAL KINETIC
ENERGY
Relation between rotational and translational K.E in aspects of work:

29. Rolling Kinetic Energy
Translation Rotation
K.E (total) = K.E (translation) + K.E (rotation)
K.Etotal = ½ mv2 + ½ I 2
Both pieces in units of Joules.

30. NEWTON SECOND LAW OF
ROTATION:
•The rotational form of Newton's second
law states the relation between net
external torque and the angular acceleration of a
body about a fixed axis. The result looks similar to
Newton's second law in linear motion with a few
modifications.

31. MODIFICATIONS:
Translational
quantity
Rotational
Analogue
Symbol
Force
Torque t
Mass
Moment of inertia I
Translational
acceleration Angular
acceleration
a

32. NEWTON'S SECOND LAW STATES “That the
angular acceleration is proportional to the net torque
and inversely proportional to the moment of inertia”.
NEWTON'S SECOND LAW:

33. ROTATIONAL FORM OF NEWTON‘S
SECOND LAW FOR POINT MASS

34. • First consider a case where all the mass
is in one place.
Suppose a point object of
mass ‘m’ attached to a light rigid rod of
length ‘l ’ is rotating about an axis
perpendicular to the rod and passing
through its end. A force acts on the
particle to increase the angular velocity of
rotation. Break the force into its
components. One component is towards
the axis and called the radial component
of force and the other component is in
the tangential direction .
• The torque of the radial component about
the axis is zero as the line of action of the
force is passing through the axis itself.
The torque of the tangential component
will try to increase the object's angular
velocity and produce angular

35. THE NET TORQUE OF THE FORCE ALONG
THE AXIS IS
The acceleration of the particle along the tangential direction will be .
For
motion along a circular path, the object's angular acceleration will be ,
Where R is the radius of the circular path of the particle, which in this case
will be the length of the rod. Thus,

36. Comparing equations (1) and (2),
Now, since the moment of inertia of a particle about the axis of rotation is we
have
t = I α

37. ROTATIONAL FORM OF NEWTON'S SECOND
LAW FOR RIGID BODY
DEFINATION :
If the relative distance between any two particles on
a body remains the same throughout the motion,
then the body is said to be rigid. Such a body
maintains its shape and size irrespective of the
forces acting on it.

38. • If a rigid body is rotating about a fixed
axis and multiple forces are acting on it
to change its angular velocity, then the
body can be to be made up of many
small point masses attached at the end
of mass less rods and rotating about
the same axis. As the body is rigid, all
the particles complete their circular
motion together and the angular
acceleration for all the particles is the
same. Applying the rotational form of
Newton's second law for individual
particles,

39. Applying the rotational form of newton's
second law for individual particles,

40. ROTATION IN DAILY LIFE