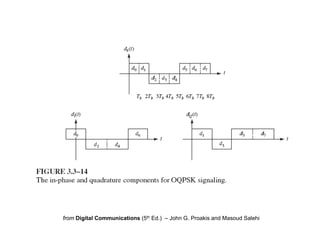
This document summarizes digital modulation techniques including CPFSK, CPM, MSK, and OQPSK. It describes the key characteristics of each technique in 1-3 sentences. CPFSK continuously shifts the carrier frequency to address spectral side lobes compared to conventional FSK. CPM generalizes CPFSK by allowing different modulation indices and waveform shapes. MSK is a special case of CPFSK where the modulation index is 1 and the waveform is rectangular, resulting in minimum frequency separation. OQPSK prevents abrupt 180 degree phase changes in QPSK by misaligning the I and Q components.

1. TELE4653 Digital Modulation &
Coding
Digital Modulation
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales

2. Outline
CPFSK
CPM
MSK
Offset QPSK
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.1/2

3. Modulation with Memory
Modulation is the mapping between the digital sequence
and the signal sequence to be transmitted over the channel.
Modulation with memory: the mapping depends on the
current and the past bits.
Example: differential encoding.
bk = ak ⊕ bk−1
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.2/2

4. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

5. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

6. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

7. CPFSK
Why do we need Continuous-Phase FSK (CPFSK)?
A conventional FSK signal is generated by shifting the
carrier by m∆f , 1 ≤ m ≤ M . It can be accomplished by
having M separate oscillators tuned to the desired
frequencies.
The abrupt switching from one oscillator output to another
results in large spectral side lobes of the signal.
To address spectral side lobes, the frequency is changed
continuously. CPFSK.
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.6/2

8. CPFSK
The signal waveform of CPFSK is given by
2E
s(t) = cos [2πfc t + φ(t; I) + φ0 ] (1)
T
where φ(t; I) represents the time-varying phase of the carrier, as
t
φ(t; I) = 4πT fd d(τ )dτ (2)
−∞
with a PAM signal
d(t) = In g(t − nT ). (3)
n
In denotes the sequence of amplitudes and g(t) is the
1
rectangular pulse of amplitude of 2T and duration of T .
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.7/2

9. CPFSK
Although d(t) contains discontinuities, φ(t; I) is continuous.
The phase φ(t; I) in the interval nT ≤ t ≤ (n + 1)T is
n−1
φ(t; I) = 2πfd T Ik + 4πfd T q(t − nT )In (4)
k=−∞
= θn + 2πhIn q(t − nT ) (5)
n−1
where h = 2fd T is the modulation index, θn = πh k=−∞ Ik
represents the accumulation of all symbols, and

 0
 t<0


q(t) = t
0≤t≤T (6)
 2T

 1

2 t>T
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.8/2

10. CPM
For continuous-phase modulation (CPM) signals,
n
φ(t; I) = 2π Ik hk q(t − kT ), nT ≤ t ≤ (n + 1)T (7)
k=−∞
where {Ik } is the sequence of M -ary symbols selected from
{±1, ±3, · · · , ±(M − 1)}, {hk } is a sequence of modulation
indices, and q(t) is some normalized waveform shape as
t
q(t) = g(τ )dτ (8)
0
Full-response CPM if g(t) = 0 for t > T , and Partial-response
CPM if g(t) = 0 for t > T .
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.9/2

11. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

12. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

13. MSK
Minimum-shift keying (MSK) is a special case of binary CPFSK
(and CPM) in which h = 1 and g(t) is a rectangular pulse of
2
duration T . The phase of the carrier in the interval
nT ≤ t ≤ (n + 1)T is [obtained from Eq. (5)]
t − nT
φ(t; I) = θn + πIn , nT ≤ t ≤ (n + 1)T (9)
2T
and the MSK signal is
s(t) = A cos [2πfc t + φ(t; I)] (10)
1 1
= A cos 2π fc + In t − nπIn + θn , (11)
4T 2
for nT ≤ t ≤ (n + 1)T .
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.12/2

14. MSK
For binary CPFSK, i.e., In = {±1}, the signal may be written as
1
si (t) = A cos 2πfi t + θn + nπ(−1)i−1 , i = 1, 2 (12)
2
where 1
f1 = fc − (13)
4T
1
f2 = fc + (14)
4T
Note ∆f = f2 − f1 = 1/2T , i.e., the minimum frequency
separation that is necessary to ensure the orthogonality of
signals s1 (t) and s2 (t). This explains why binary CPFSK with
h = 1 is called the MSK.
2
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.13/2

15. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

16. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

17. Offset QPSK
For conventional QPSK signals, the possible 180◦ phase
change can occur when both I and Q components change
simultaneously.
To prevent 180◦ phase changes that cause abrupt changes
in the signal, resulting in large spectral side lobes, offset
QPSK (OQPSK) is introduced, by misalignment of the I and
Q components. The OQPSK signal can be written as
∞
s(t) = A I2n g(t − 2nT ) cos 2πfc t
n=−∞
∞
+ I2n+1 g(t − 2nT − T ) sin 2πfc t (15)
n=−∞
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.16/2

18. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

19. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi

20. OQPSK vs. MSK
Conventional QPSK contains phase jumps of ±180◦ or
±90◦ .
Offset QPSK contains phase jumps of ±90◦ . It has constant
frequency, but there exist jumps in its waveform.
MSK may be represented as a form of OQPSK.
MSK has continuous phase, so there exist no jumps in the
waveform. But there are jumps in its instantaneous
frequency.
GMSK can smooth the frequency jumps of MSK by shaping
the lowpass signal before being applied to the MSK
modulator.
TELE4653 - Digital Modulation & Coding - Lecture 2. March 15, 2010. – p.19/2

21. from Digital Communications (5th Ed.) – John G. Proakis and Masoud Salehi