This document discusses an integrate-and-dump detector used in digital communications. It describes the operation of the integrate-and-dump detector, showing how it integrates the received signal plus noise over each symbol interval. The output of the integrator is used to detect whether a 1 or 0 was transmitted. An expression is derived for the probability of detection error in terms of the signal amplitude, noise power spectral density, and symbol interval. An example is also provided to calculate the error probability for a given binary signaling scheme and system parameters.

1. TELE3113 Analogue and Digital
Communications –
Detection Theory (2)
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales
7 Oct. 2009 TELE3113 1

2. Integrate-and-Dump detector
Integrate-and-Dump detector
r(t)=si(t)+n(t)  s (t ) = + A 0≤t ≤T for 1
si (t ) =  1
s2 (t ) = − A 0≤t ≤T for 0
t 0 +T
 a1 (t ) + no for 1
Output of the integrator: z (t ) = ∫ [si (t ) + n(t )]dt = 
t 0 +T
t0 a2 (t ) + no for 0
where a1 = ∫ Adt = AT
t0
t 0 +T
a2 = ∫ (− A)dt = − AT
t0
t 0 +T
no = ∫ n(t )dt
t0
7 Oct. 2009 TELE3113 2

3. Integrate-and-Dump detector
no is a zero-mean Gaussian random variable.
t0 +T
  t 0 +T

E{no } = E  ∫ n(t )dt  = ∫ E{n(t )}dt = 0
 t0
  t0

  t 0 +T  
2

{ }
σ no = Var{no } = E no = E  ∫ n(t )dt  
2 2 
  t0

 
 
t o +T t 0 +T
= ∫ ∫ E{n(t )n(ε )}dtdε
t0 t0
t o +T t 0 +T
η
= ∫ ∫ δ (t − ε )dtdε
t0 t0
2
t 0 +T
η ηT
= ∫
t0
2
dε =
2
1 1
pdf of no: f n (α ) =
−α 2 /( 2σ no )
2 2
e = e −α /(ηT )
o
2π σ no πηT
7 Oct. 2009 TELE3113 3

4. Integrate-and-Dump detector
 s1 (t ) = + A 0≤t ≤T for 1
As si (t ) = 
s 0 (t ) = − A 0≤t ≤T for 0 s0 s1
We choose the decision threshold to be 0. 0
− AT + AT
Two cases of detection error:
(a) +A is transmitted but (AT+no)<0 no<-AT
(b) -A is transmitted but (-AT+no)>0 no>+AT
Error probability:
Pe = P (no < − AT | A) P ( A) + P (no > AT | A) P (− A)
− AT 2 ∞ 2
e −α /(ηT )
e −α /(ηT )
= P ( A)
−∞
∫ πηT
dα + P (− A) ∫
AT πηT
dα
∞ 2
e −α /(ηT )
 2 A2T 
dα [P( A) + P (− A)]
∞ 2
e −u / 2
= ∫ πηT
Thus, Pe = Q

 Q Q(x ) = ∫ du
AT
 η   x 2π
∞ 2
e −u / 2 2α  2 Eb 
= ∫
T
du Qu =
2π ηT = Q
 η 
 Q Eb = ∫ A2 dt
2 A2T η
  0
7 Oct. 2009 TELE3113 4

5. Integrate-and-Dump detector
Consider two signal symbols s1 and s2.
Let Ed be the energy of the difference signal (s1- s2),
s2 s1
T
 Ed  signal symbol energy=si2
Ed = ∫ [s1 (t ) − s2 (t )] dt Pe = Q 
2
i.e.  2η 
0  
 s (t ) = + A 0≤t ≤T for 1
For example: If si (t ) =  1
s2 (t ) = − A 0≤t ≤T for 0
T T
Thus Ed = ∫ [s1 (t ) − s2 (t )] dt = ∫ [A − (− A)] dt = 4 A T
2 2
2
0 0
 4 A2T   2 A2T 
⇒ Pe = Q  = Q 
 2η   η 
   
7 Oct. 2009 TELE3113 5

6. Integrate-and-Dump detector
Example: In a binary system with bipolar binary signal which is a +A volt or –A volt pulse
during the interval (0,T), the sending of either +A or –A are equally probable.
The value of A is 10mV. The noise power spectral density is 10-9 W/Hz. The
transmission rate of data (bit rate) is 104 bit/s. An integrate-and-dump detector
is used.
(a) Find the probability of error, Pe.
(b) If the bit rate is increased to 105 bit/s what value of A is needed to
attain the same Pe, as in part (a).
η
Solution: (a) With = 10 −9 , P(+A)=P(-A)=0.5 , bit interval T=10-4 seconds, A=10mV
2
 2 A 2T   −4 
( )
−3 2
Pe = Q  = Q 2(10 × 10 ) (10 )  = Q 10 = 7.8 × 10 − 4
 η   2 × 10 −9 
   
 
( )
2
(b) Bit interval T=10 -5 seconds, for the same P , i.e. P = Q 2 A T  = Q 10
e e
 η 
 
2 A 2T
= 10 → A=
(
10 2 × 10 −9 )
= 31.62mV
η 2 10 −5 ( )
7 Oct. 2009 TELE3113 6

7. Optimal Detection Threshold
Pe = P (detect s 2 | s1 ) P( s1 ) + P (detect s1 | s 2 ) P( s 2 )
λ ∞
= P ( s1 ) ∫ f (r | s1 )dr + P( s 2 ) ∫ f (r | s 2 )dr
−∞ λ
λ
 λ 
= P ( s1 ) ∫ f (r | s1 )dr + P( s 2 ) 1 − ∫ f (r | s 2 )dr 
−∞  −∞ 
λ
= P( s 2 ) + ∫ [P(s ) f (r | s ) − P(s
−∞
1 1 2 ) f (r | s 2 )]dr
7 Oct. 2009 TELE3113 7

8. Optimal Detection Threshold
To find a threshold λo which minimizes Pe, we set dPe = 0
dλ
gives
Taking ln(.) on both sides, then
P( s1 ) f (λo | s1 ) = P ( s 2 ) f (λo | s 2 )
λo (s1 − s2 ) s12 − s2
2
P(s )
f (λo | s1 ) P ( s 2 ) − = ln 2
= σn 2
2σ n2
P(s1 )
f (λo | s 2 ) P( s1 )
o o
s +s σn 2
P(s )
− ( λo − s1 ) 2 /( 2σ no )
2 λo − 1 2 = o ln 2
f (λo | s1 ) e P( s 2 ) 2 s1 − s2 P(s1 )
= −( λ − s ) 2 /( 2σ 2 ) =
s1 + s2 σ no
2
f (λ o | s 2 ) e o 2 no P( s1 ) λo = +
P(s )
ln 2
2 s1 − s2 P(s1 )
2 2 2 2
λo ( s1 − s2 ) / σ no − ( s1 − s 2 ) /( 2σ no ) P( s 2 )
e = If P ( s1 ) = P ( s 2 ) ⇒ λo =
s1 + s 2
P ( s1 ) 2
7 Oct. 2009 TELE3113 8

9. Correlator Receiver
r r 2
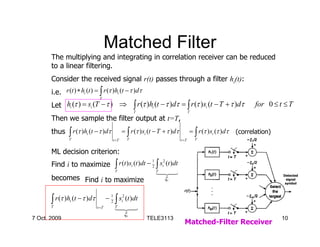
Recall ML decision criterion: minimize r − si
r r
= ∫ [r (t ) − si (t )] dt = ∫ r 2 (t )dt + ∫ − 2 ∫ r (t ) si (t )dt
2
With r − si
2
si2 (t )dt
T T T T
1 24
4 3 1 24
4 3
constant energy of i - th signal
r r
∫ si2 (t )dt − 2 ∫ r (t ) si (t )dt
2
minimize r − si minimize
T T
Let ξ i denotes the energy of si(t).
ML decision criterion becomes
Detected
Find i to maximize signal
∫ r (t ) si (t )dt − 1 ∫ si2 (t )dt symbol
2
T T
1 24
4 3
ξi
Or simply: Find i to maximize ∫ r (t )s (t )dt
T
i
if all signal symbols have the same energy
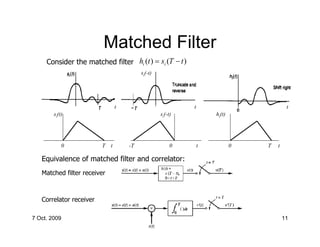
Correlation Receiver
7 Oct. 2009 TELE3113 9

10. Matched Filter
The multiplying and integrating in correlation receiver can be reduced
to a linear filtering.
Consider the received signal r(t) passes through a filter hi(t):
i.e. r (t ) ∗ hi (t ) = ∫ r (τ )hi (t − τ )dτ
T
Let hi (τ ) = si (T − τ ) ⇒ ∫ r (τ )h (t − τ )dτ = ∫ r (τ )s (t − T + τ )dτ
i i for 0 ≤ t ≤ T
T T
Then we sample the filter output at t=T,
thus ∫ r (τ )h (t − τ )dτ
T
i = ∫ r (τ ) si (t − T + τ )dτ
T
= ∫ r (τ ) si (τ )dτ
T
(correlation)
t =T t =T
ML decision criterion:
∫ r (t ) s (t )dt − ∫ s
1 2
Find i to maximize i 2 i(t )dt
T T
1 24
4 3
becomes Find i to maximize ξi
Detected
signal
symbol
∫ r (τ )h (t − τ )dτ
T
i − 1 ∫ si2 (t )dt
2
T
t =T 1 24
4 3
ξi
7 Oct. 2009 TELE3113 10
Matched-Filter Receiver

11. Matched Filter
Consider the matched filter hi (t ) = si (T − t )
si(-t)
t t t
si(t) si(-t) hi(t)
0 T t -T 0 t 0 T t
Equivalence of matched filter and correlator:
Matched filter receiver
≤ ≤
Correlator receiver
7 Oct. 2009 TELE3113 11

12. Detection of PAM
Detection of M-ary PAM (one-dimension)
symbol s1 s2 sM/2-1 sM/2 sM/2+1 sM/2+2 sM-1 sM
… …
amplitude −3 E − E 0 E 3 E ( M − 1) E
2
Let si = E Ai where i = 1,2 ,...,M and Ai = (2i − 1 − M ) , energy of si is si
For equally probable signals, i.e. P( si ) = 1 / M
for i = 1,2,...,M
1 M 2 E M 2 E M E M (M 2 − 1)  M 2 − 1 
average energy ε av = ∑ si = ∑ Ai = ∑ (2i − 1 − M ) = =
 3 E
2
M i =1 M i =1 M i =1 M 3 
 
Received signal r = si + n = E Ai + n where n = 0, σ n = η 2
2
Average Prob(symbol error) Pe =
M −1
M
(
P r − si > E )
∞
M −1 2
πη ∫E
2
= e − x η dx
M
2( M − 1)  2 E 
∞
x 2 M −1 2
∫ Q 
2
let y = = e − y 2 dy =  η 
η M 2π 2 E /η
M  
7 Oct. 2009 TELE3113 12

13. Detection of QAM
…
Detection of M-ary QAM (two-dimension) : M=2k 2E
For one-dimension M -ary PAM:
2E
Average Prob(symbol error) Pe ( M − PAM ,1D )
… …
2( M − 1)  2 E 
= Q
 η 

M  
For two-dimension M-ary QAM:
Average Prob(correct decision) Pc ( M −QAM , 2 D ) = 1 − Pe ( ( ) 2
…
M − PAM ,1D )
Average Prob(symbol error) Pe ( M −QAM , 2 D ) = 1 − Pc ( M −QAM , 2 D )
 2E 
(
= 1 − 1 − Pe ( M − PAM ,1D )
)
2
For M=4, Pe ( 4 − PAM ,1D ) = Q
 η 

 
Average Prob(symbol error) Pe ( 4−QAM , 2 D ) = 1 − 1 − Pe ( ( 4 − PAM ,1D )
)
2
2
  2 E   2E   2 E 
= 1 − 1 − Q
 η 
  = Q
 η 
  2 − Q
 η 


      
7 Oct. 2009 TELE3113 13