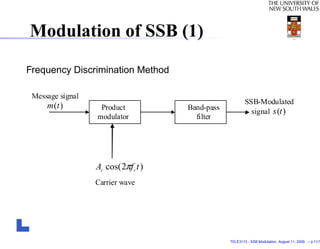
This document discusses single sideband (SSB) modulation. It begins by reviewing double sideband suppressed carrier (DSB-SC) modulation and how SSB modulation is derived from DSB-SC by suppressing one of the sidebands. It then provides the mathematical expressions for upper SSB and lower SSB modulation. The document also covers the Hilbert transform and how it relates to SSB modulation. It describes the spectra of upper and lower SSB signals and two methods for modulating SSB: frequency discrimination and phase discrimination. Finally, it discusses demodulation of SSB signals.

1. TELE3113 Analogue and Digital
Communications
SSB Modulation
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales

2. Last week ...
We have studied:
Amplitude Modulation:
s(t) = [1 + ka m(t)]c(t).
Simple envelope detection, but low power efficiency.
DSB-SC Modulation:
s(t) = m(t)c(t).
High power efficiency, but requiring a perfect phase
recovery for coherent detection.
Both AM and DSB-SC have two symmetric sidebands in the
modulated wave, thereby causing the wastage of bandwidth.
TELE3113 - SSB Modulation. August 11, 2009. – p.1/1

3. From DSB-SC to SSB (1)
First, let us review DSB-SC modulation of a single-tone
message signal m(t) = Am cos(2πfm t). The modulated signal is
sDSB (t) = m(t)c(t) = Am Ac cos(2πfm t) cos(2πfc t)
1 1
= Am Ac cos[2π(fc + fm )t] + Am Ac cos[2π(fc − fm )t].
2 2
The FT of the DSB-SC modulated signal is given by
Am Ac Am Ac
SDSB (f ) = δ(f − fc − fm ) + δ(f + fc + fm )
4 4
Am Ac Am Ac
+ δ(f − fc + fm ) + δ(f + fc − fm ).
4 4
TELE3113 - SSB Modulation. August 11, 2009. – p.2/1

4. From DSB-SC to SSB (2)
Suppose that we want to generate a sinusoidal SSB modulated
wave that retains the upper side-frequency at fc + fm . By
suppressing the second term in the equation of s DSB (t), we get
1
sUSSB (t) = Am Ac cos[2π(fc + fm )t].
2
It can be further expressed as (using the trigonometric identity
cos(x + y) = cos x cos y − sin x sin y)
1
sUSSB (t) = Am Ac cos(2πfc t) cos(2πfm t)
2
1
− Am Ac sin(2πfc t) sin(2πfm t).
2
TELE3113 - SSB Modulation. August 11, 2009. – p.3/1

5. From DSB-SC to SSB (3)
Suppose that we want to generate a sinusoidal SSB modulated
wave that retains the lower side-frequency at fc − fm . By
suppressing the first term in the equation of sDSB (t), we get
1
sLSSB (t) = Am Ac cos[2π(fc − fm )t].
2
We further express it as
1
sLSSB (t) = Am Ac cos(2πfc t) cos(2πfm t)
2
1
+ Am Ac sin(2πfc t) sin(2πfm t).
2
TELE3113 - SSB Modulation. August 11, 2009. – p.4/1

6. From DSB-SC to SSB (4)
Combining the equations of sUSSB (t) and sLSSB (t), we get the
SSB modulated wave of a single-tone message signal
m(t) = Am cos(2πfm t) as follows:
1
sSSB (t) = Am Ac cos(2πfc t) cos(2πfm t)
2
1
Am Ac sin(2πfc t) sin(2πfm t),
2
where the minus and plus signs apply to the upper SSB and
lower SSB, respectively.
TELE3113 - SSB Modulation. August 11, 2009. – p.5/1

7. SSB
For a periodic message signal m(t) = m am cos(2πfm t),
the SSB modulated wave is
1
sSSB (t) = Ac cos(2πfc t) am cos(2πfm t)
2 m
1
Ac sin(2πfc t) am sin(2πfm t).
2 m
Generally, for a Fourier transformable message signal m(t),
the SSB modulated wave is
1 1
sSSB (t) = Ac m(t) cos(2πfc t) Ac m(t) sin(2πfc t),
ˆ
2 2
ˆ
where m(t) is Hilbert transform of m(t). (See next page)
TELE3113 - SSB Modulation. August 11, 2009. – p.6/1

8. Hilbert Transform (1)
ˆ
The signal m(t) is the Hilbert transform of the signal m(t),
defined as
1 ∞ m(τ )
m(t) =
ˆ dτ
π −∞ t − τ
1
= m(t) . (convolution)
πt
If m(t) ⇔ M (f ), then
ˆ
m(t) ⇔ M (f ) = −jsgn(f )M (f ),
ˆ

 1, f > 0



where the sign function is sgn(f ) = 0, f = 0


 −1, f < 0

TELE3113 - SSB Modulation. August 11, 2009. – p.7/1

9. Hilbert Transform (2)
1
m (t ) h (t ) = m(t )
ˆ
πt
Illustration of Hilbert transform in time domain
M(f ) H ( f ) = − j sgn( f ) ˆ
M(f )
Illustration of Hilbert transform in frequency domain
TELE3113 - SSB Modulation. August 11, 2009. – p.8/1

10. Hilbert Transform (3)
Note that the frequency response of Hilbert transformer
1
h(t) = πt is
H(f ) = −jsgn(f ).
The magnitude of H(f ) is given by

 1, f > 0
|H(f )| =
 1, f < 0
and the phase is given by 
 −90◦ , f > 0
∠H(f ) =
 90◦ , f < 0
TELE3113 - SSB Modulation. August 11, 2009. – p.9/1

11. Spectra of SSB
For positive frequencies, the spectra of the two kinds of SSB
modulated waves are as follows:
For the upper SSB,

 Ac M (f − f ), f ≥ fc
2 c
S(f ) =
 0, 0 < f < fc
For the lower SSB,

 0, f ≥ fc
S(f ) =
 Ac M (f − fc ), 0 < f < fc
2
TELE3113 - SSB Modulation. August 11, 2009. – p.10/1

12. Modulation of SSB (1)
Frequency Discrimination Method
Message signal
SSB-Modulated
m (t ) Product Band-pass
signal s (t )
modulator filter
Ac cos( 2πf c t )
Carrier wave
TELE3113 - SSB Modulation. August 11, 2009. – p.11/1

13. Modulation of SSB (2)
Phase Discrimination Method
+
Message signal SSB-Modulated
m(t ) Product signal s (t )
∑
modulator
cos(2πf c t ) m
Oscillator
Wideband − 900
Phase-shifter
Phase-shifter
sin(2πf c t )
ˆ
m (t )
Product
modulator
TELE3113 - SSB Modulation. August 11, 2009. – p.12/1

14. Demodulation of SSB
Modulated Demodulated
wave s (t ) v(t ) signal v o (t )
Product Low-pass
modulator filter
Ac' cos(2πf c t + φ )
Local
oscillator
Suppose in the receiver the local oscillator can provide the
same frequency, but arbitrary phase difference φ,
measured with respect to the carrier wave c(t).
It applies equally well to the demodulation of both DSB-SC
and SSB.
TELE3113 - SSB Modulation. August 11, 2009. – p.13/1