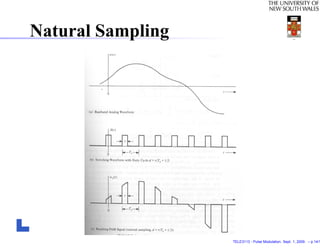
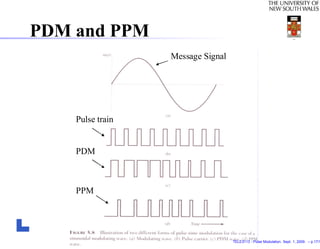
This document discusses pulse modulation techniques in communications. It begins by reviewing continuous-wave modulation techniques studied previously, such as amplitude modulation and angle modulation. It then previews that pulse modulation will be studied next, including analog pulse modulation where a pulse feature varies continuously with the message, and digital pulse modulation using a sequence of coded pulses. The document provides explanations and equations regarding sampling of continuous-time signals, the sampling theorem, and recovery of the original analog signal from its samples. It also introduces pulse amplitude modulation (PAM) using natural and flat-top sampling, as well as pulse duration modulation (PDM) and pulse position modulation (PPM).

1. TELE3113 Analogue and Digital
Communications
Pulse Modulation
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales

2. What did we study
In previous lectures, we studied continuous-wave (CW)
modulation:
Some parameter of a sinusoidal carrier wave is varied
continuously in accordance with the message signal.
Amplitude Modulation (AM, DSB-SC, SSB, VSB)
Angle Modulation (PM, FM)
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.1/1

3. What will we study
Next, we will study Pulse Modulation:
Some parameter of a pulse train is varied in accordance
with the message signal.
Analogue pulse modulation: some feature of the pulse
(e.g. amplitude, duration, or position) is varied continuously
in accordance with the sample value of the message signal.
Digital pulse modulation: the message signal is discrete
in both time and amplitude, thereby transmitting a sequence
of coded pulses.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.2/1

4. Sampling Process 1
Let ga (t) be a continuous-time (CT) signal that is sampled
uniformly at t = nT , generating the sequence g[n],
g[n] = ga (nT ), −∞ < n < ∞ (1)
where T is the sampling period and n is an integer.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.3/1

5. Sampling Process 2
Sampling
ga(t) g[n]
ga(t) gp(t)
p(t)
∞
p(t) is a periodic impulse train: p(t) = n=−∞ δ(t − nT ).
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.4/1

6. Sampling Process 3
p(t) can be expressed as a Fourier series as (see page 18 for
details)
∞
1 2π
p(t) = exp(j( )kt). (2)
T T
k=−∞
The sampling operation is a multiplication of the continuous-time
signal ga (t) by a period impulse train p(t):
∞
1 2π
gp (t) = ga (t) · p(t) = ga (t) · exp(j( )kt) . (3)
T T
k=−∞
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.5/1

7. FT of Sampled Signal
Assume Ga (jω) ⇔ ga (t), i.e., Ga (jω) = F [ga (t)]. From the
frequency-shifting property of the FT, we have
2π 2π
F [ga (t) · exp(j( )kt)] = Ga (j(ω − k )). (4)
T T
Next, taking FT on both sides of (3) and using (4), we get
∞
1
Gp (jω) = F [gp (t)] = Ga (j(ω − kωT )), −∞ < k < ∞ (5)
T
k=−∞
2π
where ωT = T denotes the angular sampling frequency.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.6/1

8. Sampling Theorem
Sampling theorem: Let ga (t) be a bandlimited signal with
Ga (jω) = 0 for |ω| > ωm . Then ga (t) is uniquely determined by
its samples ga (nT ), −∞ < n < ∞, if
ωT ≥ 2ωm , (6)
where
2π
ωT = . (7)
T
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.7/1

9. Signal Recovery 1
Question: Suppose that g[n] is obtained by uniformly sampling
a bandlimited analog signal ga (t) with a highest frequency ωm at
a sampling rate ωT = 2π satisfying (6), can the original analog
T
signal ga (t) be fully recovered from the given sequence g[n]?
Answer: YES, ga (t) can be fully recovered by generating an
impulse train gp (t) and then passing gp (t) through an ideal low
pass filter (LPF) H(jω) with a gain T and a cutoff frequency ω c
satisfying ωm < ωc < ωT − ωm .
∧
g[n] gp(t) LPF g a(t)
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.8/1

10. Representation in Spectrum
G a ( jω )
ω
− ωm ωm
Sampling
Recovery
LPF G p ( jω )
•••
•••
ω
− ωT ωT 2ωT
ωm ωc
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.9/1

11. Signal Recovery 2
Taking the inverse FT of the frequency response of the ideal LPF
H(jω):

 T, |ω| ≤ ω
c
H(jω) = (8)
 0, |ω| > ωc
Then, the impulse response h(t) of the LPF is given by
ωc
1 ∞
jωt T
h(t) = H(jω)e dω = ejωt dω
2π −∞ 2π −ωc
sin(ωc t)
= . (9)
πt/T
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.10/1

12. Signal Recovery 3
Consider the impulse train gp (t) be expressed as
∞
gp (t) = ga (t) · p(t) = ga (t) · δ(t − nT )
n=−∞
∞ ∞
= ga (nT )δ(t − nT ) = g[n]δ(t − nT ). (10)
n=−∞ n=−∞
Therefore, the output of the LPF is given by the convolution of
gp (t) with the impulse response h(t):
∞
ga (t) =
ˆ g[n]h(t − nT ). (11)
n=−∞
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.11/1

13. Signal Recovery 4
Substituting h(t) from (9) in (11) and assuming for simplicity
ωc = ωT /2 = π/T , we arrive at
∞
sin[π(t − nT )/T ]
ga (t) =
ˆ g[n]
n=−∞
π(t − nT )/T
∞
t − nT
= g[n] · sinc( ), (12)
n=−∞
T
where sinc(x) is defined as sinc(x) = sin(πx)/(πx).
The reconstructed analog signal ga (t) is obtained by shifting in
ˆ
time the impulse response of the LPF h(t) by an amount nT and
scaling it an amplitude by the factor g[n] for −∞ < n < ∞ and
then summing up all shifted versions.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.12/1

14. PAM
Pulse-amplitude modulation (PAM): The amplitudes of
regularly spaced pulses are varied in proportion to the
corresponding sample values of a continuous message signal.
Generation of PAM:
Natural Sampling: easy to generate, only an analog switch
required.
Flat-Top Sampling: generated by using a sample-and-hold
(S/H) type of electronic circuit.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.13/1

15. Natural Sampling
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.14/1

16. Flat-top Sampling
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.15/1

17. PDM and PPM
Pulse-duration modulation (PDM): The duration of the
pulses are varied according to the sample values of the
message signal. Also referred to as pulse-width modulation
or pulse-length modulation.
Pulse-position modulation (PPM): The leading or trailing
edge of each pulse is varied in accordance with the
message signal.
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.16/1

18. PDM and PPM
Message Signal
Pulse train
PDM
PPM
TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.17/1

19. Derivation of Eq. (2)
Using Fourier series, p(t) can be expressed as
∞
k
p(t) = ck exp(j2π t),
T
k=−∞
where T /2
1 k
ck = p(t) exp(−j2π t)dt
T −T /2 T
T /2 ∞
1 k
= δ(t − nT ) exp(−j2π t)dt
T −T /2 n=−∞
T
T /2
1 k
= δ(t) exp(−j2π t)dt
T −T /2 T
1
= . (13)
T TELE3113 - Pulse Modulation. Sept. 1, 2009. – p.18/1