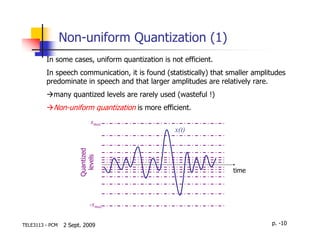
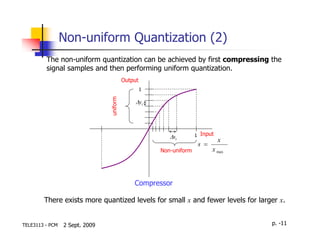
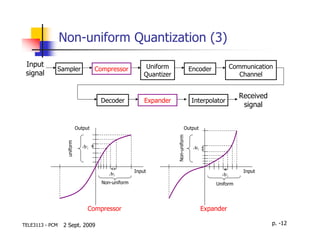
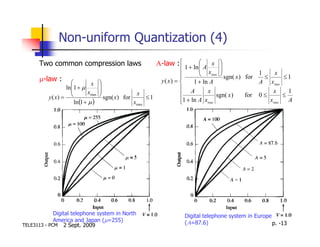
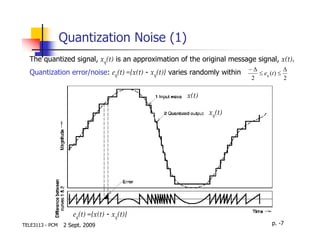
This document discusses quantization in analog-to-digital conversion. It describes how an analog signal is sampled, quantized by representing samples with discrete levels, and encoded into a digital signal. Quantization introduces noise that can be reduced by using more quantization levels or a smaller step size between levels. Non-uniform quantization allocates more levels to signal amplitudes that occur more frequently to more efficiently represent the signal.

1. TELE3113 Analogue and Digital
Communications – Quantization
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales
TELE3113 - PCM 2 Sept. 2009 p. -1

2. Analog-to-Digital Conversion
Goal: To transmit the analog signals by digital means better performance
convert the analog signal into digital format (Pulse-Code Modulation)
Analog sampler Quantizer Encoder Digital
signal signal
1111111
1111110
1111101
1111100 1111101 1111001 1111001 1111011 1111101 1111110 1111101 1111001
1111011
1111010 c8 c7 c6 c5 c4 c3 c2 c1
x(t) 1111001
1111000
time
time time
Sampling: a continuous-time signal is sampled by measuring its
amplitude at discrete time instants.
Quantizing: represents the sampled values of the amplitude by a finite set
of levels
Encoding: designates each quantized level by a digital code
TELE3113 - PCM 2 Sept. 2009 p. -2

3. Reconstruction of Sampled Signal
1111101 11110011111001 1111011 1111101 1111110 11111011111001
Received
digital signal c8 c7 c6 c5 c4 c3 c2 c1
time
decoding
Recovered signal
with discrete levels
interpolation
Recovered
analog signal
TELE3113 - PCM 2 Sept. 2009 p. -3

4. Sampling
Consider an analog signal x(t) which is bandlimited to B (Hz), that is:
X ( f ) = 0 for | f |≥ B
The sampling theorem states that x(t) can be sampled at intervals as
large as 1/(2B) such that the it is possible to reconstruct x(t) from its
samples, or the sampling rate fs=1/Ts can be as low as 2B.
x(t) 1
f s ≥ 2B or Ts ≤
2B
Sampling rate fs=1/Ts
time
Sampling period Ts
Minimum required sampling rate=2B (Nyquist rate) i.e. 2B samples per second
Sampling rate should be equal or greater than twice the highest frequency in
the baseband signal.
TELE3113 - PCM 2 Sept. 2009 p. -4

5. Analogue Pulse Modulation
Pulse Amplitude
Modulation
Pulse Duration
(Width) Modulation
Pulse Position
Modulation
TELE3113 - PCM 2 Sept. 2009 p. -5

6. Quantization
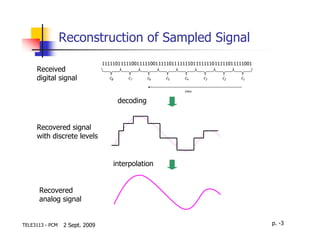
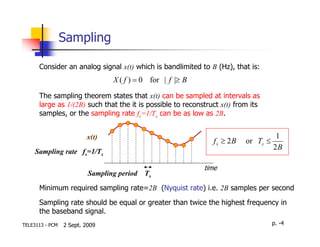
After the sampling process, the sampled points will be transformed into a
set of predefined levels (quantized level) Quantization
Assume the signal amplitude of x(t) lies within [-Vmax ,+Vmax], we divide the
total peak-to-peak range (2Vmax) into L levels in which the quantized
levels mi (i=0,…,(L-1)) are defined as their respective mid-ways.
Vmax xq(t) x(t)
Output
m7 ∆7
m7= 7∆/2
m6 ∆6
uniform
m6= 5∆/2
m5 ∆5 m5= 3∆/2
m4 ∆4 m4= ∆/2
m3 ∆3 time −4∆ −3∆ −2∆ −∆ ∆ 2∆ 3∆ 4∆ Input
m2 ∆2
−3∆/2
uniform
m1 ∆1 −5∆/2
m0 ∆0 −7∆/2
-Vmax
Sampling time
Uniform quantizer
2Vmax (midrise type)
For uniform quantization, ∆ i ( i =0 ,L,( L −1)) = ∆ =
L p. -6
TELE3113 - PCM 2 Sept. 2009

7. Quantization Noise (1)
The quantized signal, xq(t) is an approximation of the original message signal, x(t).
−∆ ∆
Quantization error/noise: eq(t) ={x(t) - xq(t)} varies randomly within ≤ eq (t ) ≤
2 2
x(t)
xq(t)
eq(t) ={x(t) - xq(t)}
TELE3113 - PCM 2 Sept. 2009 p. -7

8. Quantization Noise (2)
Assume the quantization error varies uniformly within [-∆/2, ∆/2]
with a pdf of f(eq)=1/∆, then
∆ 2 ∆ 2
2
q [ ]
e (t ) = ∫ f (eq ) eq (t ) deq =
2 1
∫
∆ −∆ 2
[ 2
eq (t ) deq ] Q f (eq ) =
1
∆
−∆ 2
3 ∆ 2
1 eq ∆2 Vmax
2
2Vmax
= = = with ∆ =
∆ 3 −∆ 2
12 3L2 L
To minimize eq(t), we can use smaller ∆ or more quantized levels L.
2
In general, the average power of a signal is x (t ) or x 2 (t )
x 2 (t ) 3L2 x 2 (t )
average SNRx = 2
= 2
eq (t ) Vmax
 3L2 x 2 (t )   V2 
average SNRx (dB) = 10 log   = 4.77 + 20 log L − 10 log 2max 
 Vmax
2
  x (t ) 
   
TELE3113 - PCM 2 Sept. 2009 p. -8

9. Quantization Noise (3)
2
Vmax
If x(t) is a full-scale sinusoidal signal, i.e. x(t)=Vmaxcosωt , then x (t ) = x (t ) = 2 2
2
Thus,
average SNRx (dB) = 4.77 + 20 log L − 10 log(2 ) = (1.76 + 20 log L ) dB
If x(t) is uniformly distributed in the range [-Vmax,+Vmax], then pdf f(x)=1/(2Vmax),
Vmax Vmax
1 1
x (t ) = ∫ f ( x)[x(t )] dx = ∫ [x(t )]2 dx
2
2
Q f (eq ) =
−Vmax
2Vmax −Vmax
2Vmax
Vmax
1 x3 2
Vmax
= =
2Vmax 3 3
Thus, −Vmax
average SNRx (dB) = 4.77 + 20 log L − 10 log(3) = 20 log L dB
TELE3113 - PCM 2 Sept. 2009 p. -9

10. Non-uniform Quantization (1)
In some cases, uniform quantization is not efficient.
In speech communication, it is found (statistically) that smaller amplitudes
predominate in speech and that larger amplitudes are relatively rare.
many quantized levels are rarely used (wasteful !)
Non-uniform quantization is more efficient.
xmax
x(t)
Quantized
levels
time
-xmax
TELE3113 - PCM 2 Sept. 2009 p. -10

11. Non-uniform Quantization (2)
The non-uniform quantization can be achieved by first compressing the
signal samples and then performing uniform quantization.
Output
1
uniform
∆yi
∆ si 1 Input
x
s =
Non-uniform x max
Compressor
There exists more quantized levels for small x and fewer levels for larger x.
TELE3113 - PCM 2 Sept. 2009 p. -11

12. Non-uniform Quantization (3)
Input Uniform Communication
Sampler Compressor Encoder
signal Quantizer Channel
Received
Decoder Expander Interpolator
signal
Output Output
Non-uniform
uniform
∆ yi ∆si
∆si Input Input
∆ yi
Non-uniform Uniform
Compressor Expander
TELE3113 - PCM 2 Sept. 2009 p. -12

13. Non-uniform Quantization (4)
Two common compression laws Α-law : 1 + ln  A x 
 
  

  xmax  sgn( x ) for 1 ≤ x ≤ 1
µ-law :   y ( x) =  1 + ln A A xmax
x
ln1 + µ


  A
xmax x x x 1
y ( x) =   sgn( x) for ≤1  sgn( x ) for 0 ≤ ≤
ln (1 + µ ) xmax 1 + ln A xmax
 xmax A
Digital telephone system in North Digital telephone system in Europe
America and Japan (µ=255) (Α=87.6)
TELE3113 - PCM 2 Sept. 2009 p. -13