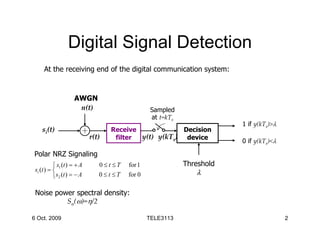
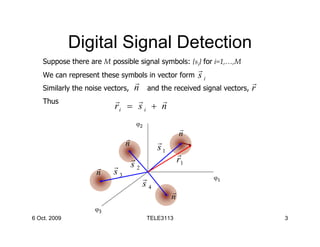
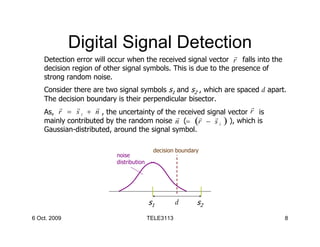
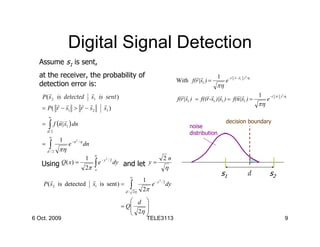
1) The document describes digital signal detection techniques at the receiver of a digital communication system. 2) It discusses the maximum a posteriori probability (MAP) and maximum likelihood (ML) detection criteria. The ML criterion reduces to choosing the signal that minimizes the Euclidean distance between the received signal vector and possible transmitted signals. 3) Detection errors occur when the received signal, distorted by noise, falls inside the decision region of another signal. The probability of error depends on the noise distribution around the actual transmitted signal.

1. TELE3113 Analogue and Digital
Communications –
Detection Theory
Wei Zhang
w.zhang@unsw.edu.au
School of Electrical Engineering and Telecommunications
The University of New South Wales
6 Oct. 2009 TELE3113 1

2. Digital Signal Detection
At the receiving end of the digital communication system:
AWGN
n(t) Sampled
at t=kTs
1 if y(kTs)>λ
si(t) Receive Decision
r(t) filter y(t) y(kTs) device
0 if y(kTs)<λ
Polar NRZ Signaling
 s (t ) = + A 0≤t ≤T for 1 Threshold
si (t ) =  1 λ
s2 (t ) = − A 0≤t ≤T for 0
Noise power spectral density:
Sn(ω)=η/2
6 Oct. 2009 TELE3113 2

3. Digital Signal Detection
Suppose there are M possible signal symbols: {si} for i=1,…,M
r
We can represent these symbols in vector form si
r r
Similarly the noise vectors, n and the received signal vectors, r
Thus r r r
ri = s i + n
ϕ2
r
r n
n r
s1
r r
s2 r1
r r
n s3
r ϕ1
s4
r
n
ϕ3
6 Oct. 2009 TELE3113 3

4. Digital Signal Detection
In each time interval, the signal detector makes a decision based on
r
the observation of the vector r so that the probability of correct
decision is maximized.
Consider a decision rule based on the posterior probabilities
r r
P(signal si was transmitted | received vector r ) for i = 1,2 ,K ,M
r r
= P( si | r )
The decision is based on selecting the signal corresponding to the
maximum set of posterior probabilities.
r r r
r r r f (r | si ) P( si )
Choose s i to maximize: P( si | r ) = r r
f (r ) where f(r ) =
M
r r r
∑ f(r | s m ) P( s m )
m =1
r r
where P ( s i ) is probability of si being transmitted and
r
f(r ) is the pdf function of
the received signal vector r .
This kind of decision is called maximum a posteriori probability (MAP) criterion
6 Oct. 2009 TELE3113 4

5. Digital Signal Detection
MAP criterion
r r r
r r f (r | si ) P( si ) r M
r r r
P( si | r ) = r where f(r ) = ∑ f(r | s m ) P( s m )
f (r ) m =1
r r
where f(r | si ) is called the likelihood function.
r
If the M symbols are equally probable; i.e. P ( si ) = 1 / M for all i, the decision
r r
rule based on finding the signal thatrmaximizes P( si | r ) is equivalent to
r
finding the signal that maximizes f(r | si ).
r r
The decision based on the maximum of f(r | si ) over M signal symbols
is called the maximum-likelihood (ML) criterion
6 Oct. 2009 TELE3113 5

6. Digital Signal Detection
r r r
Recall: r = si + n
For AWGN, the noise {nk} components are uncorrelated Gaussian
variables which are statistically independent
E[nk ] = 0 (zero mean) , E[rk ] = E[sik + nk ] = sik
η η
Variance σ n = E[n 2 ] − (E[n]) = → σ r2 = σ n =
2 2 2
2 2
Thus {rk} are statistically independent Gaussian variables
r r N
f(r | si ) = Π f(rk | sik ) where N is number of base vectors
k =1 1 2 2
/( 2σ n )
and f(rk | sik ) = e −( rk − sik )
2π σ n
1 − ( rk − sik ) 2 / η
= e
πη
Take natural logarithm on both sides, gives
r r −N 1 N
ln(πη ) − ∑ (rk − sik )
2
ln f(r | si ) =
6 Oct. 2009 2
TELE3113 η k =1 6

7. Digital Signal Detection
r r −N 1 N
ln(πη ) − ∑ (rk − sik )
2
ln f(r | si ) =
2 η k =1 r r r
With ln(•) is a monotonic function, the maximum of f(r | si ) over s i is
r
equivalent to finding the signal s i that minimizes the Euclidean distance:
N
r r
D(r , si ) = ∑ (rk − sik ) 2
k =1
r r
So, the ML decision criterion (maximize f(r | si ) over M signal symbols, i.e.
r
i=1,…M) reduces to finding the signal s i that is the closest in distance to
r
the received signal vector r .
Example: 3 signal symbols.
Note the decision regions formed by
the perpendicular bisectors of any
two signal symbols.
6 Oct. 2009 TELE3113 7

8. Digital Signal Detection
r
Detection error will occur when the received signal vector r falls into the
decision region of other signal symbols. This is due to the presence of
strong random noise.
Consider there are two signal symbols s1 and s2 , which are spaced d apart.
The decision boundary is their perpendicular bisector.
r r r r
As, r = s i + n , the uncertainty of the received signal vector r is
r r r
mainly contributed by the random noise n (= (r − s i ) ), which is
Gaussian-distributed, around the signal symbol.
decision boundary
noise
distribution
s1 d s2
6 Oct. 2009 TELE3113 8

9. Digital Signal Detection
Assume s1 is sent,
at the receiver, the probability of rr 1 −( r r
r − s1 )2 /η
With f(r |s1 ) = e
detection error is: πη
r r rr rr r rr 1 −( r
P ( s 2 is detected s1 is sent ) f(r |s1 ) = f((r -s1 )|s1 ) = f(n|s1 ) = e
n )2 /η
r r r r r πη
= P ( r − s1 > r − s 2 s1 )
∞
rr
= ∫ f (n |s1 ) dn noise
decision boundary
d/ 2
distribution
∞
1
∫
2
/η
= e −n dn
d /2 πη
∞
1 2n
∫
2
Using Q ( x) = e−y /2
dy and let y =
2π x η
∞
s1 d s2
r r 1 − y2 / 2
P ( s2 is detected s1 is sent ) = ∫ 2π
e dy
d / 2η
 d 
= Q 
 2η 
 
6 Oct. 2009 TELE3113 9

10. Digital Signal Detection
r
For a signal symbol set: {si } for i = 1,...M
Detection error probability is
M
r r
Pe = ∑ P[erroneous detection|si sent ]P[ si ]
i =1
r r
M M  s k − si  r
≤ ∑∑ Q   P[ si ]
i =1 i ≠ k  2η
 

k =1
r
If all signal symbols are equally probable, i.e. P[ si ] = 1 / M
M
r r
Pe = ∑ P[erroneous detection|si sent ]P[ si ]
i =1
r r
1 M M s k − si 
≤ ∑∑ Q  2η
M i =1 i ≠ k 

 

k =1
6 Oct. 2009 TELE3113 10

11. Digital Signal Detection
Calculation of error probabilities:
(
(a) Antipodal signaling: s1 = + E ,0 ; s2 = − E ,0) ( )
Pe = P ( s 2 is detected | s1 ) P ( s1 ) + P ( s1 is detected | s 2 ) P ( s 2 )
2 E   
≤Q   P ( s1 ) + Q 2 E  P ( s 2 )
 2η   2η 
    s2 s1
 2E 
= Q  [P ( s1 ) + P ( s 2 )]
 η  − E + E
 
 2E 
= Q
 η 
 signal symbol energy=E
 
Example: for NRZ signaling which takes amplitude either +A or 0. For bit
interval Tb, the energy per bit Eb=A2Tb.
 A2T   
Pe = Q  = Q Eb 
 η   η 
6 Oct. 2009  TELE3113 
  11

12. Digital Signal Detection
(
(b) Orthogonal signaling: s1 = + E ,0 ; s2 = 0,+ E ) ( )
Pe = P( s 2 is detected | s1 ) P( s1 ) + P( s1 is detected | s 2 ) P ( s 2 ) + E s2
 2E   
≤ Q  P( s1 ) + Q 2 E  P( s 2 ) s1
 2η   2η 
   
+ E
 E   E
= Q
 
[P(s1 ) + P( s 2 )] = Q 
 η
 η  
(c) Square signaling:
s1 = + ( ) ( ) (
E ,− E ; s2 = + E ,+ E ; s3 = − E ,+ E ; s4 = − E ,− E) ( )
4
Pe = ∑ P ( si is not detected | si ) P ( si ) s3 + E s2
i =1
 2 E
     

4
≤ ∑ P ( si )Q  + Q 2 2 E  + Q 2 E
  2η   2η   2η 
i =1       
 − E + E
 2E   E s4 − E s1

= 2Q  + Q 2 
  η
6 Oct. 2009  η    TELE3113 12

13. Digital Signal Detection
Integrate-and-Dump detector
r(t)=si(t)+n(t)  s (t ) = + A 0≤t ≤T for 1
si (t ) =  1
s2 (t ) = − A 0≤t ≤T for 0
t 0 +T
 a1 (t ) + no for 1
Output of the integrator: z (t ) = ∫ [si (t ) + n(t )]dt = 
t 0 +T
t0 a2 (t ) + no for 0
where a1 = ∫ Adt = AT
t0
t 0 +T
a2 = ∫ (− A)dt = − AT
t0
t 0 +T
no = ∫ n(t )dt
t0
6 Oct. 2009 TELE3113 13

14. Digital Signal Detection
no is a zero-mean Gaussian random variable.
t0 +T
  t 0 +T

E{no } = E  ∫ n(t )dt  = ∫ E{n(t )}dt = 0
 t0
  t0

  t 0 +T  
2

{ }
σ no = Var{no } = E no = E  ∫ n(t )dt  
2 2 
  t0

 
 
t o +T t 0 +T
= ∫ ∫ E{n(t )n(ε )}dtdε
t0 t0
t o +T t 0 +T
η
= ∫ ∫ δ (t − ε )dtdε
t0 t0
2
t 0 +T
η ηT
= ∫
t0
2
dε =
2
1 1
pdf of no: f n (α ) =
−α 2 /( 2σ no )
2 2
e = e −α /(ηT )
o
2π σ no πηT
6 Oct. 2009 TELE3113 14

15. Digital Signal Detection
 s1 (t ) = + A 0≤t ≤T for 1
As si (t ) = 
s 0 (t ) = − A 0≤t ≤T for 0 s0 s1
We choose the decision threshold to be 0. 0
− AT + AT
Two cases of detection error:
(a) +A is transmitted but (AT+no)<0 no<-AT
(b) -A is transmitted but (-AT+no)>0 no>+AT
Error probability:
Pe = P (no < − AT | A) P ( A) + P (no > AT | A) P (− A)
− AT 2 ∞ 2
e −α /(ηT )
e −α /(ηT )
= P ( A)
−∞
∫ πηT
dα + P (− A) ∫
AT πηT
dα
∞ 2
e −α /(ηT )
 2 A2T 
dα [P( A) + P (− A)]
∞ 2
e −u / 2
= ∫ πηT
Thus, Pe = Q

 Q Q(x ) = ∫ du
AT
 η   x 2π
∞ 2
e −u / 2 2α  2 Eb 
= ∫
T
du Qu =
2π ηT = Q
 η 
 Q Eb = ∫ A2 dt
2 A2T η
  0
6 Oct. 2009 TELE3113 15