The document provides information about Expert Systems and Solutions, including their contact details and areas of expertise. They are calling for research projects from final year students in fields like electrical engineering, electronics and communications, power systems, and applied electronics. Students can assemble hardware projects in the company's research labs with guidance from experts.

1. EXPERT SYSTEMS AND SOLUTIONS
Email: expertsyssol@gmail.com
expertsyssol@yahoo.com
Cell: 9952749533
www.researchprojects.info
PAIYANOOR, OMR, CHENNAI
Call For Research Projects Final
year students of B.E in EEE, ECE,
EI, M.E (Power Systems), M.E
(Applied Electronics), M.E (Power
Electronics)
Ph.D Electrical and Electronics.
Students can assemble their hardware in our
Research labs. Experts will be guiding the
projects.

2. Multirate digital signal
processing
• The rapid development of multirate digital
signal processing is complemented by the
emergence of new applications. These
include subband coding of speech, audio,
and video signals, multicarrier data
transmission, fast transforms using digital
filter banks and discrete wavelet analysis of
all types of signals.
2

3. Multirate algorithms
• A key characteristic of multirate algorithms
is their high computational efficiency. In
many cases, these algorithms are the prime
reason that an application can now be
implemented economically using modern
digital signal processors
3

4. 1 Sampling Rate Conversion
• Many different sampling rates in the
system
⇒ Reduction of computational complexity.
• What happens when the sampling rate is
changed?
4

5. 1.1.1 Discrete sampling
Discrete signals are often described using the
complex number
W M
= exp (-j2π/M) = M 1 (1.1)
This is one of the M different M-th roots of 1,
since W M
M
=1
On the unit circle of the complex plane:
5

6. Figure 1.1 Definition of WM
Im
2π/M
Z WM
0 1
Z Re
2π/M
6

7. Figure 1.2 Sampling of a discrete
signal
a) x(n)
0 12 3 4 5 n
15
w4(n)
b)
n
x(n)w4(n)
c) n
1 234 5 15 7

8. Figure 1.3 Sampling with a phase
offset of λ =3
a) x(n)
0 12 3 4 5 n
15
b) w4(n- λ)
n
x(n)w4(n- λ)
c)
n
1 2 34 5 15 8

9. The sampling function
1 M −1 νn 1 for n = mM, m integer
WM (n) = ∑ WM = (1.2)
M ν =0  0 otherwise
Note:
1 M −1
w M (n) = w M (−n) = M ∑ W M− νn
(1.3)
ν =0
With the phase offset λ:
1 M −1 1 for n = λ + mM, m intger
w M (n − λ) = M ∑ W M =  0
ν(n − λ)
(1.4)
ν =0  otherwise

10. 1.1.2 Polyphase Representation
It is possible to sample M different
signals out of x(n) each having every
Mth sample of the original .
(p) (p) (p) (p)
x(n) = x 0
(n) +x x 1 x (n)
(n) +
2
(n) +
3
(1.5)
= x(n) w (n) + x(n) w (n − 1) + x(n) w (n − 2) + x(n) w (n − 3)
4 4 4 4
Or in general,
M −1 M −1
x(n) = ∑ x λ (n) = ∑ x (n) ⋅ w M (n − λ)
(p)
(1.6)
λ =0 λ =0

11. The z-transform
∞
X(z) = ∑ x(n) ⋅ z-n (1.7)
n = −∞
Can likewise be partitioned into M sub-signals. For example, for the
finite signal x(n) in Fig. 1.4, we have
X(z) = x(0)z -0 + x(4)z -4 + x(8)z -8 + x(12)z -12
+ x(1)z -1 + x(5)z -5 + x(9)z -9 + x(13)z -13
+ x(2)z -2 + x(6)z -6 + x(10)z -10 + x(14)z -14
+ x(3)z -3 + x(7)z -7 + x(11)z -11 + x(15)z -15 (1.8)

12. −λ
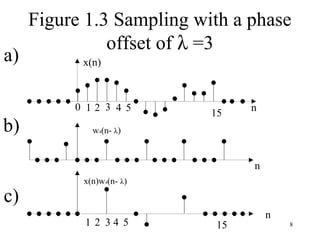
Taking out factor of z , λ = 0.....3, gives
[
-0 -0 -4 -8
x( z ) = z x(0) z + x(4) z + x(8) z + x(12) z ] -12
+ z [ x(1) z + x(5) z + x(9) z + x(13) z ]
-1 -0 -4 -8 -12
+ z [ x(2) z + x(6) z + x(10) z + x(14) z ]
-2 -0 -4 -8 -12
+ z [ x(3) z + x(7) z + x(11) z + x(15) z ]
-3 -0 -4 -8 -12
(1.9)
These are polynomials in z-4
12

13. Figure 1.4
Polyphase representation of a
discrete signal (next slide):
13

14. x(n)
n
0 12 3 4 5 15
x 0(p)(n) x 1(n)
n λ=0
x 1(p)(n)
λ=1
n
x 2(p)(n)
λ=2
n
x 3(p)(n)
λ=3
n
14

15. n = m⋅M + λ
M -1 ∞ M −1
X(z) = ∑ ∑ x(mM + λ). z = ∑z
-(mM + λ) −λ (p) M
⇒ X λ
(z ) (1.10)
λ =0 m = - ∞ λ =0
where
∞
∑ x(mM + λ) ⋅ z -mM
(p) M
X λ
(z ) =
m =−∞
(1.11)
Equation (1.10) is called the
polyphase representation of the z-
transform X(z)
15

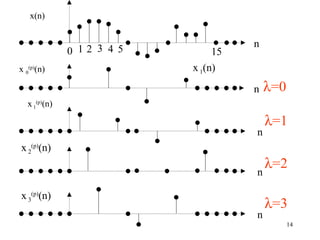
16. First polynomial :
(p) −0 −1 −2 −3
x 0
( z ) = x(0) z + x(4) z + x(8) z + x(12) z (1.12)
One-to-one Mapping
z n
-λ ( p) M ( p)
z xλ ( z ) xλ (n), λ = 0,1,2.... M - 1 (1.13)
Vector Form :

X
(p)
(z) = [X (p)
0
(z), z
−1
X
1
(p)
(z),...., z
− (M −1)
X
(p)
M −1
(z) ]
T
(1.14)
16

17. Replacing λ by M - 1 - λ leads to the type 2 polyphase representation
[ Vai 88b] :
M −1
X(z) = ∑ z
− (m −1− λ) (p2) M
λ =0
X λ
(z ) (1.15)
Where
∞
∑x
(p2) M (p2) − mM
X (z λ
)=
m =-∞
λ
(m). z (1.16)
and
(p2)
x λ
(m) = x(mM + M − 1 − λ) (1.17)
17

18. The type 1 and type 2 representations are related by
(z) = x M −1− λ (z),
(p2) (p)
x λ
λ = 0,1,2........ M - 1 (1.18)
(p) (p2)
The signals x1 (n) from Fig.1.4c and x 2 (n)
are therefore identical. Only the indexing is done
in the reverse order.
Replacing λ by - λ the type 3 polyphase
representation will be obtained
from the standard representation [ Cro 83] :
18

19. = ∑ z X (z )
M -1
X(z) (1.19)
λ (p3) M
λ
λ =0
Where
= ∑ x (m) z
∞
(p3)
X z
λ
M
m = −∞
(p3)
λ
− mM
(1.20)
and
x (m) = x(mM − λ) (1.21)
(p3)
λ
The type 1 and type 3 representations are related by
x (z) = x (z) (1.22)
(p3) (p)
0 0
and
x (z) = z x (z), λ = 1,2,3........M − 1 (1.23)
(p3) −1 (p)
λ M −λ
The signals x (n) in fig 1.4c and x (n) are therefore identical
(p)
1
(p3)
3
19

20. 1.1.3 Modulation Representation
Multiply the argument z by W k
M
(m)
X (e
k
X(z W ), k = 0,1,2....M -1
jΩ
)=
k
M
(1.24)
jΩ
Z → e ( Fourier Transform)
X (e ) = X(e e ) = X(e
(m) jΩ jΩ - j2π k/M j[ Ω - 2π k/M]
) (1.25)
k

2π k
Modulation = shifting the frequency by
M
20

21. In The Time Domain
X(z ⋅ W )
k
M ( W ) ⋅ x(n)
k
M
= x(n) ⋅ exp(j2π kn/M) (1.26)
= x(n) ⋅ cos(2π kn/M) + jx(n) ⋅ sin(2π kn/M)
21

22. Figure 1.5
Modulation representation
of a signal X(e jΩ
)
22

23. (m)
X = X
a) 0
k =0
Ω
0 π /M π 2π
b) (m)
x 1
k =1
Ω
0 2π / M π 2π
c) x
(m)
2 k =2
Ω
0 4π / M 2π
d) (m)
x 3 k =3
Ω
0 6π / M 2π
23

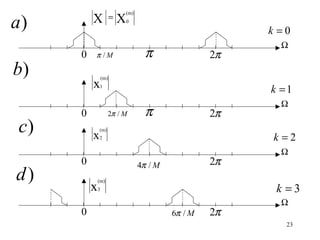
24. To avoid complex Time Domain signals
we have to combine
X(z W k
M
) + X(z W M )
M -k
W
- kn
M
kn
x(n) + W M x(n)
= 2x(n) ⋅ cos(2π kn/M) (1.27)
The complete set of modulated z - Transforms
in the Matrix form :
x
(m)
(z) = [x (m)
0
(z) x 1
(m)
(z) ...... x
(m)
M −1
(z) ] T
(1.28)
∞
∑X
-λ (p) M (p) −n
z X λ
(z ) =
m = −∞
λ
.z (1.29)
24

25. 1.1.4 Transformation of the
signal Components
From (1.13):
(p)
x λ
(n) = x(n) ⋅ w M (n − λ)
1 M −1
= x(n) ⋅ ∑ W M
ν(λ − n)
(1.30)
M ν =0
25

26. substituting the expression in
(1.30) into equation (1.29) gives,
replacing ν by k,
∞
1 M −1
z-λ X (p) (
λ z
M
)= ∑∞ x(n) ⋅ ∑ W k(λ −n). z−n
M
n =- M k =0
1 M −1 ∞ k(λ − n)
= ∑ n∑ x(n) ⋅z ⋅W M
M k =0 = −∞
−n
1 M −1  ∞ 
-n
∑ n∑ x(n)⋅(zWM 
k kλ
=   ⋅ WM (1.31)
M k =0  = −∞
  


(z) W M ) = Xk x(z
(m) k
26

27. The relationship between the polyphase components
and the modulation components is thus
the following
k =0
M W k ∑X λ M
z X z
(z) ⋅ ( )=
λk (m)
M −1
(p) M 1 −λ (1.32)
Using DFT Matrix
(p) 1 (m)
x (z) =
M
⋅ W ⋅x M
(z). (1.33)
27

28. Reducing the Sampling Rate
Decimation
≈ ↓M
ANTI-ALIASING
28

29. 1.2.1 Downsampling
The sampling rate of a discrete signal x(n) is
reduced by a factor M by taking only every
M-th value of the signal. The relationship between
the resulting signal y(m) and
the original signal x(n) is as follows:
y(m) = x(mM) (1.34)
Fig1.6 shows a signal flow representation of this
process:
29

30. Figure 1.6 Downsampler
x(n) y(m)
↓M
30

31. Can also be described using the polyphase
representation using discrete sampling
function w M (n) and leaving out the zeroes.
In the z-domain, we can use the z-transform of
the original signal,
∞
X(z) = ∑x(n) ⋅ z -n
(1.35)
n =−∞
and (1.11) with λ = 0, to obtain the z - transform
∞
x0 (z M ) = ∑x(m ⋅ M) ⋅ z−mM
(p)
m =−∞
∞ −m
= ∑ ( )
y(m) ⋅ z M
m =−∞
=Y z ( )M
= Y ( z′) (1.36) 31

32. Figure 1.7
steps in signal
processing used to perform
downsampling
32

33. a) x(n)
0 12 3 4 5 n
15
→T ←
b) (p)
x 0
( n)
x ( 0) → ← x(4) ← x(12)
n
1 234 5 15
c)
y(m)
x ( 0) → ← x(4) ← x(12)
1 3 4
←4T →
m 33

34. Leaving out the zero values can be explained
Y(z ) = Y(z′)
M
y(m). (1.37)
using Laplace plane
z=e sT
(1.38)
The space between samples is now
T′ = MT (1.39)
and so we can define a new variable
z′ = e sT ′
(1.40)
from (1.39), the relationship between the two variables
is then
z′ = z M
(1.41)
34

35. Example 1.1 :
The z - transform of the signal x(n) in fig 1.7a is given by
X(z) = x(0) + x(1) z + x(2) z + .... + x(14) z + x(15) z
−1 −2
(1.42)−14 −15
The polyphase component with λ = 0 in fig.1.7b is
X ( z ) = x(0) + x(4) z + x(8) z + x(12) z (1.43)
(p) 4 −4 −8 −12
0
From this , we get the polynomial
Y( z ) = x(0) + x(4)( z ) + x(8)( z ) + x(12)( z )
−1 −2 −3
4 4 4 4
(1.44)
and thus the z - transform of the downsampled signal in fig. 1.7c,
Y(z′) = x(0) + x(4)( z′) + x(8)( z′) + x(12)( z′)
−1 −2 −3
(1.45)
35

36. 1.2.2 Spectrum of the
Downsampled Signal
The z - transform of the discretely sampled signal Y(z ) M
in (1.36) can be expressed using modulation components.
From (1.32) with λ = 0 ,
we obtain
1
Y( z ) = ∑ X(z W )
M -1
M k
M (1.46)
M k =0
For stable signals, the substitution z → e jΩ
helps us derive the discrete - time Fourier transform
1
Y(e ) = ∑ X( e
M -1
jMΩ
) (1.47)
jΩ − j2π k/M
M k =0
36

37. In the following, the magnitude of this
transform is referred to
as the magnitude spectrum,
often shortened to just spectrum.
37

38. Fig1.8 spectra obtained using
downsampling
(m)
X = X 0 ←→ must be bandlimited
0 π /M π 2π Ω
Y
↓ k = 0 ↓ k =1 ↓ k = 2 ↓ k = 3 ↓ k = 0 Ω
0 2π / M 4π / M 6π / M 2π
0 π 2π 2πM Ω′
38

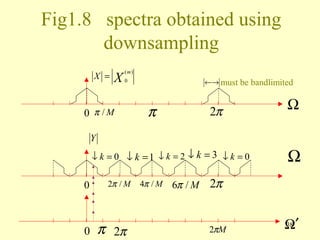
39. Normalised Sampling Rate is 2π
Magnitude is decreased by factor M
2π
New sampling rate
M
⇒ s = jω
e =e =e =e (1.48)
jMΩ jMω T jωT ′ jΩ ′
The normalized frequency Ω′ = MΩ (1.49)
corresponds time spacing T′
Spectrum in terms of Ω′
1
⇒ Y(e ) = ∑ X(e
M −1
j Ω′ j[ Ω′− 2π k]/M
) (1.50)
M k =0
39

40. Example 1.2 :
Consider a signal which has been sampled at a frequency
f = 1/T and then downsampled by a factor of M . We wish
o
to find the value of the spectrum at the frequency
f = f /(6M). The corresponding normalised
1 o
frequency is :
Ω
1 = ω T = 2π f T = π/(3M)
1 1 (1.51)
40

41. We can similarly calculate the normalized frequency
with respect to the new normalized frequency :
Ω = w T′ = 2π f T = π/3 (1.52)
/
1 1 1
Substituting the Ω from (1.51) into (1.47) gives the same
1
result as substituting Ω from (1.52) into (1.50), namely
/
1
1
Y(e ) = ∑ X(e
M -1
jπ /3
) (1.53)
jπ /3M - j2π k/M
M k =0
This is also shown in fig. 1.8b.
41

42. 1.2.3 Aliasing Effects
(Vierastumisilmiöt)
x(n)
u(n)
h(n) ↓M y(m)
Fig 1.9 Decimator consisting of an anti-
aliasing filter h(n) and
a down-sampler M
42

43. a) U not band - limited
Signal
to (π / M) ↓
0 π /M π 2π Ω
Anti-aliasing
b) H filter
0 π /M π 2π
Ω
c)
X Band-limited
Signal
0 π /M π 2π Ω
Fig 1.10 The effect of anti-aliasing
43
low-pass filter

44. After Filtering:
x(n) = u (n) * h(n) = ∑ u (k ) ⋅ h(n − k ),
∞
k = −∞
(1.54)
will be down sampled
y(m) = ∑ u (k ) ⋅ h(mM − k ).
∞
k = −∞
(1.55)
44

45. In the z-transform Domain:
X(z) = H(z) ⋅ U(z) (1.56)
From (1.46), the z - transform of the decimated signal
is then :
1
Y(z ) = ∑ H(z W ) ⋅ U(z W )
M −1
M K
M
K
M (1.57)
Mk =0
45

46. 1.2.4 Scaling of the Anti-
Aliasing Filter
The gain of the Anti-aliasing filter=?
Consider the sampled analog signal
x(n) = x ( nT ).
a (1.58)
The periodic spectrum of the discrete signal x(n)
is then
1
X(e ) = ∑ X ( jω − jn ω ),
∞
x(n) jωT
a 0
T n =−∞
ω = 2π /T
0 (1.59)
46

47. We can similarly consider the decimated signal
y(m) in (1.34) to have been obtained by sampling
the same continuous signal x (t) , but this time
a
with a sample spacing of MT :
y(m) = x (mMT) a (1.60)
The corresponding periodic spectrum is
y(n) Y(e )
jω MT
1
=
∞
∑ x (jω - jn ω /M)
a o (1.61)
MT n = −∞
47

48. By comparing the two spectra (1.59) and (1.61)
in the baseband, where the index n of the summed
expressions is 0 :
1
X ( e ) = X ( jω ) (1.62)
jωT
o a
T
and
1
Y (e ) = X ( jω), (1.63)
jωMT
o a
MT
1
∴scaling factor =
M 48

49. 1.2.5 Decimation of Band-pass
Signals
modulation
Band - pass signal
X (z) = X(z ⋅ W ),  integer (1.64)
(m) 
 M
is formed from the Baseband Signal by
a frequency shift of ΔΩ = 2π/M
49

50. (m)
X = X 1
Ω
0 π /M π 2π
↓ k = −1↓ k = 0 ↓ k = 1 ↓ k = 2 ↓ k = 3
2π / M 4π / M 6π / M 2π Ω
Figure 1.11 Spectra of decimated
band –pass signals 50

51. Downsampling the band - pass signal X(z ⋅ W ) 
M
by a factor M gives the same result as
a corresponding downsampling of the
baseband signal X(z).
substituting the band - pass signal X(z ⋅ W ) into

M
(1.46) and (1.47) , instead of X(z), gives
Y(z ) =
M -1
M 1 ∑ X(z WM W k ) (1.65)
M k =0 M
and
Y(e ) =
M -1
jMΩ 1 ∑ X(e jΩ− j2π (  + k)/M ) (1.66)
M k =0 51

52. a) U
0 2π / M π 2π Ω
b) H
0 π 2π
Ω
c) X
0 π 2π Ω
Figure 1.12 The effect of anti-
aliasing band-pass filtering 52

53. X(z ⋅ W ) is periodic in Ω

M (period 2π )
∴ It is identical to the spectrum in (1.47)
with the index k shifted by  = 1
Anti-Aliasing Band-pass
Filter is needed
53

54. 1.2.6 Downsampling with
a phase offset
Phase offest λ will be introduced :
y λ (m) = x(m ⋅ M + λ), λ = 0,1,2 ... M − 1 (1.67)
54

55. x(n)
n
0 12 3 4 5 15
x 2(p)(n) λ=2
polyphase component
15 n
y2(m)
m
λ/M 1+ λ / M 3+ λ / M
Figure 1.13 Downsampling
with a phase offset 55

56. z - transform (1.13)
z x (z ) x (n) (1.68)
-λ (p) M (p)
λ λ
From (1.32), this can be written using
the components defined in (1.24) :
X ( z ) = ∑ X(zW ) ⋅ W
M −1
z
-λ (p)
λ
M
k =0
k
M
kλ
M (1.69)
From here, we can set z = e jΩ
to deduce the spectrum of the polyphase
components x (n) : (p)
λ
M −1
1
M ∑ X(e
k =0
jΩ - j2π k/M
) ⋅W kλ
M (1.70) 56

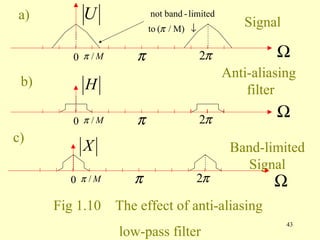
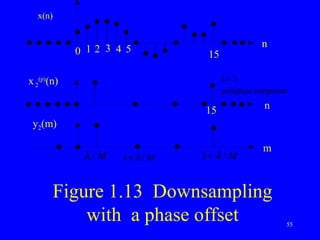
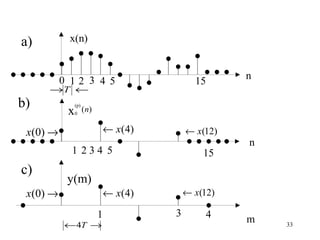
57. fig 1.13a shows the signal x(n), already given
in the fig 1.2a, and fig 1.13b the polyphase
components x (n). From here, we can obtain
(p)
2
the downsampled signal y (m) shown 2
in fig. 1.13c, by replacing z by Z or M
Ω by Ω / M , respectively (see section 1.2.1).
Its spectrum is therefore
y (m)
λ Y (e ) λ
jΩ
= 1 ∑ X(e j[ Ω−2 πk ] / M ) ⋅ W kλ
M −1
M k =0 M (1.71)
57

58. The nonzero values of the downsampled polyphase
components will not appear at integeral values
λ
of m unless λ =0. This is shown in fig 1.13c. This
representation is occasionally used for
hypothetical filter prototypes.
58

59. Example 1.3:
Consider the finite real signal x(n) in the Fig 1.14a,
whose spectrum X(exp j Ω ) is shown in the Fig
1.15a, the non-causal signal is even, i.e. x(n)= x(-n).
The spectrum is thus real and has even symmetry.
59

60. x(n)
n
0 1 2
~
x λ=0
0
m
0 1
~
x
1
λ=1
m
0 1/2 3/2 7/2
Figure 1.14 Downsampled
polyphase components with M=2
60

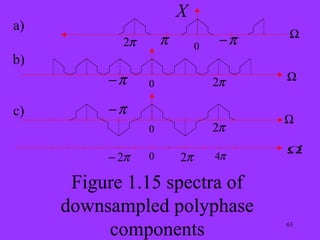
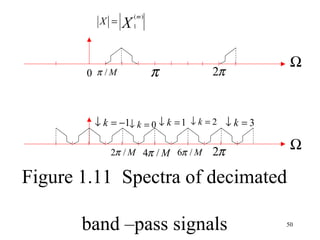
61. Fig 1.14b shows the downsampled component ~ (m), (p)
0 x
i.e. for λ = 0 . Substituti ng M = 2 into (1.70), we obtain
the spectrum :
~
11
x
(p)
0 ∑ X(e ) j[Ω −πk]
(1.72)
2
k =0
This spectrum is shown in fig 1.15b. The two sum terms
combine to form a real spectrum with a period Ω = π
or Ω′ = 2ππrespctivly. This result is seen to be compatible
with having a phase offest λ = 0 and having reduced the
sampling rate by afactor of 2 (see section 1.2.2).
~ 1 1
x
(p)
1 ∑ X(e ) W ,
j[Ω −πk]
 (1.73)
K
2
2k =0
( −1)
k
61

62. This is displayed in Fig 1.15c. Comparing (1.72) with (1.73)
or Fig.1.15b with fig 1.15c reveals that two spectra
have the same magnitude, but that with a phase
offest λ = 1 the two sum terms have opposite signs .
As a result, the spectrum of ~ (m) has a period
x
(p)
1
Ω = 2π or Ω′ = 4π . Introducing a phase offset
λ ≠ 0 does not affect the period of the spectrum.
It is evdent that this is always true.
62

63. X
a)
Ω
2π π 0
−π
b)
−π 2π Ω
0
c) −π
Ω
0 2π
Ω′
− 2π 0 2π 4π
Figure 1.15 spectra of
downsampled polyphase
components 63

64. Zero Padding = insert zeroes
between existing samples
M=4
M=5
64