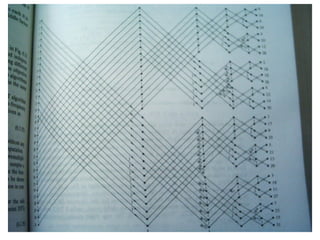
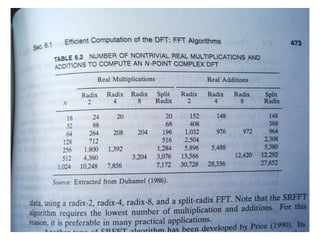
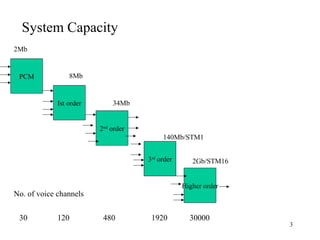
Frequency division multiplexing (FDM) divides the available bandwidth into non-overlapping frequency bands, with each band carrying a separate signal. Time division multiplexing (TDM) divides signals into different time slots to share the same frequency channel. TDM samples voice frequency signals at 8 kHz and quantizes each sample to 8 bits, requiring 64 kbps per voice channel. A 32-channel PCM system using TDM requires 2 Mbps of bandwidth and can carry more voice channels than FDM with the same bandwidth.

1. FDM vs TDM
Frequency division multiplexing(Analog Exchange)
•
•
•
•
•
•
1 chl
300 Hz to 3400 Hz
3chls : Basic Group(BG): 12 – 24 KHz
12chls: Sub Group : 4BG: 60 -108KHz
60chls:SuperGroup:5SubGp: 312 – 552 KHz
900chls:Master Group:16 super Gp 312 – 4028 KHz
2700chls:Super Master Group: (3 MG):312 -12336
KHz
1

2. Time division multiplexing
•
•
•
•
•
Voice frequency 4KHZ
Sampling rate 8kilo samples per second
Each sample requires 8bits
1 voice frequency requires 64kbps
32 voice frequencies (PCM) requires
2Mbps
2

3. System Capacity
2Mb
PCM
8Mb
Ist order
34Mb
2nd order
140Mb/STM1
3rd order
Higher order
No. of voice channels
30
120
2Gb/STM16
480
1920
30000
3

4. Chapter 2
Discrete-Time signals and systems
•
•
•
•
•
Representation of discrete-time signals
(a)Functional
(b)Tabular
(c)Sequence
Examples of singularity functions
Impulse, Step and Ramp functions and shifted
Impulse, Step and Ramp functions
4

5. Energy and power signals
• If E=infinity and P= finite then the signal is
power signal
• If E=finite and P= zero then the signal is
Energy signal
• If E=infinite and P= infinite then the signal
is neither energy nor power signal
5

6. Periodic and non-periodic signals
• X(n+N) = x(n) for all n, and N is the
fundamental time period.
6

7. Block diagram Representation of
Discrete-Time systems
•
•
•
•
•
•
•
Adder
A constant multiplier
A signal multiplier
A unit delay element
A unit advance element
Folding
Modulator
7

8. Classcification of Discrete-time
systems
•
•
•
•
•
•
Static vs dynamic systems
Time invariant vs time-variant systems
Linear vs nonlinear systems systems
Causal vs non causal systems
Stable vs unstable systems
Recursive vs non recursive systems
8

9. Static vs dynamic systems
• A discrete time system is called static or
memoryless if its output at any instant ‘n’
depends at most on the input sample at the
same time, but not on past or future samples
of the input. In any other case, the system is
said to be dynamic or to have memory.
9

10. Time invariant vs time-variant
systems
• A system is called time-invariant if its
impute-output characteristics do not change
with time.
• X(n-k)
y(n-k)
10

11. Linear vs nonlinear systems systems
• Linear system obeys the principle of
superposition
• T[a x1(n) + b x2(n)] = a T[x1(n)] + b T[x2(n)]
11

12. LTI system
• The system which obeys both Linear
property and Time invariant property.
12

13. Causal vs non causal systems
• A system is said to be causal if the output of
the system at any time depends only on
present and past inputs, but not depend on
future inputs. If a system doesnot satisfy
this definition , it is called noncausal
system.
• All static systems are causal systems.
13

14. Stable vs unstable systems
• An arbitrary relaxed system is said to be
bounded input – bounded output (BIBO)
stable if an only if every bounded input
produces a bounded output.
• y(n) = y2(n) + x(n) where x(n)=δ(n)
14

15. Recursive vs non recursive systems
• Recursive system uses feed back
• The output depends on past values of
output.
15

16. Interconnection of discrete time
systems
•
•
•
•
Addition/subtraction
Multiplication
Convolution
Correlation (a) Auto (b) Cross correlation
16

17. Convolution
• Used for filtering of the signals in time
domain. Used for LTI systems only
• 1.comutative law
• 2.associative law
• 3.d17istributive law
17

18. 18

19. Correlation
• Auto correlation improves the signal to
noise ratio
• Cross correlation attenuates the unwanted
signal
19

20. Digital signal Distortion
Distortion less transmission y(n) = α.x(n-l)
20

21. Random signal vs Deterministic
signal
• Deterministic signal: can be represented in
mathematical form since the present, past
and future values can be predicted based on
the equation
• Random signal: can not be put in
mathematical form. Only the average, rms,
peak value and bandwidth can be estimated
with in a given period of time.
21

22. Advantages of digital over analog
signals
•
•
•
•
•
•
Faithful reproduction by reshaping
Information is only 2 bits (binary)
Processed in microprocessor
Signals can be compressed
Error detection and correction available
Signals can be encrypted and decrypted
22

23. Disadvantages
• Occupies more bandwidth
• Difficult to process the digital signals in
microwave frequency range since the speed
of the microprocessor is limited (3 GHz)
• Digital signals have to be converted into
analog signals for radio communication.
23

24. Advantages of Digital signal processing
over analog signal processing
•
•
•
•
•
•
•
•
Flexible in system reconfiguration
Accuracy , precise and better tolerances
Storage
Low cost
Miniaturization
Single micro processor
Software operated (programmed)
Artificial intelligence
24

25. Multi channel and Multidimensional
Signals
• Multichannel:
• S(t) = [ s1(t), s2(t), s3(t)…]
• Multi Dimensional: A value of a signal is a
function of M independent variables.
• S(x,y,t) = [ s1(x,y,t), s2(x,y,t), s3(x,y,t)…]
25

26. Analog-discrete-digital-PCM
•
•
•
•
•
•
Analog frequency
Demo of Time and frequency signals
Digital frequency
Periodic and aperiodic signals
Sampling theorem
A to D / D to A conversion
26

27. Variable sampling rate
27

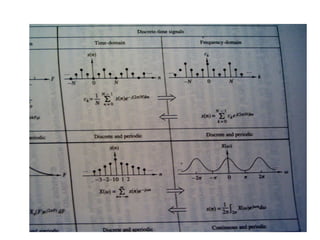
28. x(t)
|X(f)|
t
0
-f
(a)
x
δ
∞
(t) =
n = -∞
δ (t-nT
s)
...
s
-2T
s
0
2T
s
4T
m
∞
1
T s
δ (f-nf
n = -∞
s
...
t
-2f
s
s
-f
0
s
fs
2f
f
s
(d)
δ
(t)
|X
s
(f)|
...
-4T
s
-2T
s
0
2T
s
4T
t
s
(e)
Ch2. Formatting
)
...
(c)
x s (t) = x(t) x
f
f
(b)
X δ (f) =
...
-4T
0
m
...
-2f
s
-f
s
-f
m
0
(f)
[Fig 2.6] Sa mp ling the orem u sing th e freq u en cy
co nvo lution pro pe rty o f the Fou rier tra nsform
fm
fs
2f
f
s
28
[6]

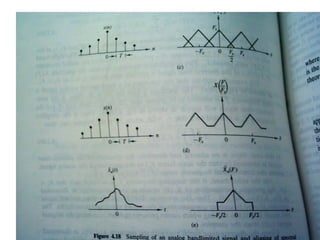
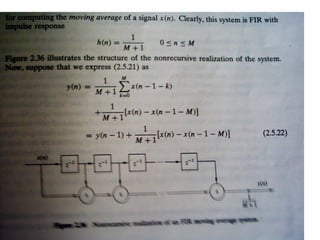
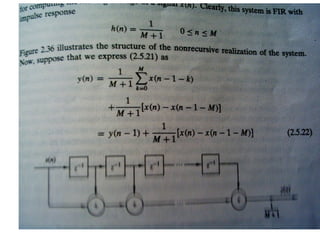
29. Sampling
• The operation of A/D is to generate sequence by taking
values of a signal at specified instants of time
• Consider a system involving A/D as shown below:
x(t )
x (t)
Analog-todigital
converter
x(nT )
x[n]
xh(t)
0
T
2T 3T 4T 5T
Digital-toanalog
converter
xh (t )
x(t) is the input signal and xh(t) is the
sampled and reconstructed signal
t
T = sample period
29

30. Impulse Sampling
What is Impulse Sampling?
– Suppose a continuous–time signal is given by x(t),
-∞ < t < +∞
– Choose a sampling interval T and read off the value of
x(t) at times nT, n = -∞,…,-1,0,1,2,…,∞
– The values x(nT) are the sampled version of x(t)
30

31. Impulse Sampling
• The sampling operation can be represented in a block
diagram as below:
∞
δ T (t ) = ∑ δ (t − nT )
n = −∞
x(t )
xS (t )
• This is done by multiplying the signal x(t) by a train of
impulse function δT(t)
• The sampled signal here is represented by xS(t) and the
sampling period is T
31

32. Impulse Sampling
• From the block diagram, define a mathematical
representation of the sampled signal using a train of δfunction
xs ( t ) =
∞
∑ x( nT )δ ( t − nT )
n = −∞
∞
= x( t ) ∑ δ ( t − nT )
n = −∞
= x ( t )δ T ( t )
continuous –time signal
function
Train of periodic impulse 32
function

33. Impulse Sampling
• We therefore have
• And
1 ∞ jnω 0t
δT (t) = ∑ e
T n = −∞
It turns out that the
problem is much
easier to understand
in the frequency
domain. Hence, we
determine the
Fourier Transform
of xs(t).
1 ∞ jnω 0t
xs ( t ) = x( t ) ∑ e
T n = −∞
1 ∞
= ∑ x ( t ) e jnω 0t
T n = −∞
33

34. Impulse Sampling
• Looking at each term of the summation, we have the
frequency shift theorem:
CTFT
x( t ) e jnω 0t ↔ X ( ω − nω 0 )
• Hence the Fourier transform of the sum is:
1 ∞
X s ( ω ) = ∑ X ( ω − nω 0 )
T n = −∞
34

35. Impulse Sampling
i.e. The Fourier transform of the sampled signal is simply
the Fourier transform of the continuous signal repeated at
the multiple of the sampling frequency and scaled by 1/T.
X(ω)
1
ω
0
Xs(ω)
1/T
-2ω0
-ω0
0
ω0
ω
2ω0 35

36. Nyquist Sampling Theorem
• The Nyquist sampling theorem can be stated as:
If a signal x(t) has a maximum frequency content (or
bandwidth) ω max, then it is possible to reconstruct x(t)
perfectly from its sampled version xs(t) provided the
sampling frequency is at least 2 × ω max
36

37. Nyquist Sampling Theorem
• The minimum sampling frequency of 2 × ωmax is known as
the Nyquist frequency, ωNyq
• The repetition of X(ω) in the sampled spectrum are known
as aliasing. Aliasing will occur any time the sample rate is
not at least twice as fast as any of the frequencies in the
signal being sampled.
• When a signal is sampled at a rate less than ωNyq the
distortion due to the overlapping spectra is called aliasing
distortion
37

38. Multichannel Tx-Rx
• Station A
cable
Station B
38

39. 39

40. Design of discrete time systems
40

41. 41

42. 42

43. 43

44. 44

45. 45

46. 46

47. 47

48. 48

49. 49

50. 50

51. 51

52. 52

53. 53

54. 54

55. 55

56. PERIODIC AND APERIODIC SIGNALS OF ANALOG AND
DISCRETE
56

57. 57

58. 58

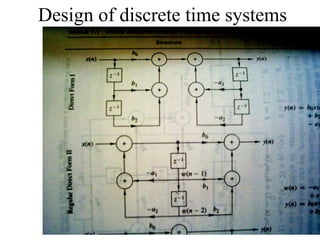
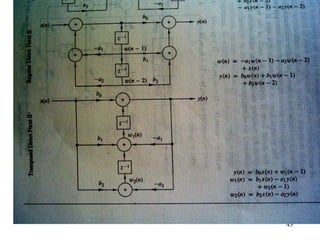
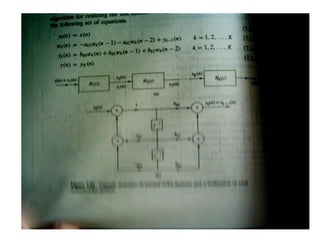
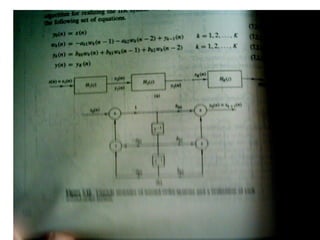
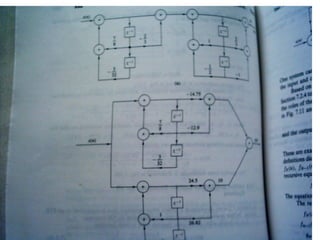
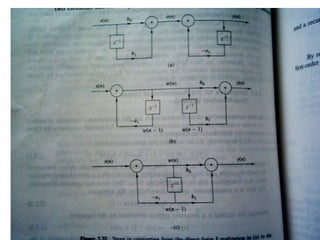
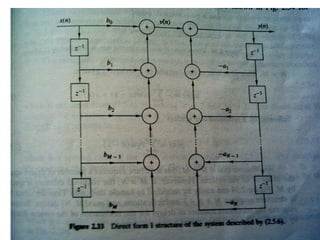
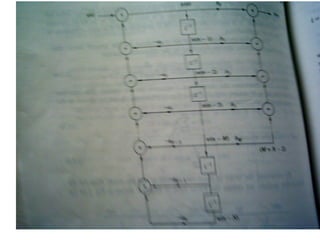
59. Computing the Z-transform: an
example = α nu[n]
x[n]
• Example 1: Consider the time function
X(z) =
∞
∑
x[n]z −n =
n=−∞
=
1
1− αz
−1 =
∞
∑
n=0
α n z −n =
∞
∑ (αz −1 )n
n=0
z
z −α
59

60. Another example …
x[n] = −α nu[−n − 1]
X(z) =
∞
∑
−1
x[n]z −n =
n=−∞
∑
−α n z −n =
n=−∞
•
∑
n=−∞
(αz −1 )n =
∑ (αz −1 )n
n=−∞
l = −n;n = −∞ ⇒ l = ∞;n = −1 ⇒ l = 1
−1
−1
∞
∞
l=1
l=0
∑ −(zα −1 )l = 1 − ∑ (zα −1 )l = 1 −
1
1
=
1 − zα −1 1 − αz −1
60

61. 61

62. 62

63. 63

64. 64

65. 65

66. 66

67. 67

68. 68

69. 69

70. 70

71. 71

72. Frequency domain of a rectangular pulse
Fourier coefficients of the rectangular pulse train with time
period Tp is fixed and the pulse width tow varies.
72

73. 73

74. 74

75. 75

76. SAMPLING IN TIME DOMAIN
76

77. 77

78. 78

79. 79

80. 80

81. 81

82. 82

83. 83

84. 84

85. 85

86. 86