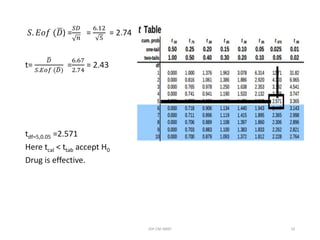
1) The document describes the unpaired t-test and paired t-test. The unpaired t-test is used to compare the means of two independent samples, while the paired t-test compares the means of two related samples or samples measured under different conditions. 2) For the unpaired t-test, the null hypothesis is that there is no difference between the population means, while the alternative hypothesis is that there is a difference. The test statistic is calculated as the difference between the sample means divided by the standard error. 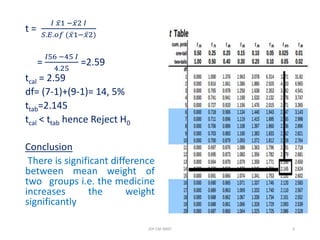3) For the paired t-test, the null hypothesis is that the mean of the differences between pairs is zero, indicating no change. The alternative hypothesis is that the mean

1. t-test
1) Unpaired/ Independent t- test
2) Paired t-test
Jagdish D. Powar
Statistician cum Tutor
Community Medicine
SMBT, IMSRC, Nashik
JDP-CM-SMBT 1

2. JDP-CM-SMBT 2
Competency SLOs(Core)
CM6.3,
Describe, discuss and demonstrate
the application of elementary
statistical methods including test of
significance in various study
designs
The student should be able to
• Write the null and alternative
hypothesis for independent t-
test and paired t-test
• Test if two sample means are
significantly different or not for
small sample sizes
• To compare difference between
paired observations
• To test whether intervention or
treatment is effective or not for
paired data.
Competency & Learning objectives

3. Unpaired/Independent t-test:-
Let x̅1 and x̅2 be the two sample means of two independent random
samples of sizes n1 and n2 drawn from two normal populations having
mean µ1 and µ2. To test the whether two population mean are equal
(n1<30, n2<30)
Null Hypothesis
Ho:- There is no significant difference between mean of two
populations i.e. µ1=µ2
H1 :- There is significant difference between mean of two
populations i.e. µ1≠µ2
Test statistics
t=
𝐼 𝑥1 −𝑥2 𝐼
𝑆.𝐸.𝑜𝑓 (𝑥1−𝑥2)
with df= (n1-1)+(n2-1)
SE of (x̅1-x̅2) =
𝑆𝐷1
𝑛1
2
+
𝑆𝐷2
𝑛2
2
Find t-table value for (n1-1)+(n2-1) df
 Decision rule, if I t I< tab t then accept Ho otherwise reject it.
JDP-CM-SMBT 3

4. JDP-CM-SMBT 4

5. 1. A group of 7 patients treated with medicine ‘A’ had mean
weight found to be 56 kg with SD of 8.22 kg. Another group
of 9 patients from the same ward of a hospital had mean
weight 45 kg with SD of 8.56. Do you claim that the medicine
increases the weight significantly?
Ans-
Given values n1=7 𝑥1= 56kg SD1= 8.22kg
n2 =9 𝑥2 =45kg SD2= 8.56kg
Ho:- There is no significant difference between mean weight of
two groups
H1 :-There is significant difference between mean weight of two
groups i.e. the medicine increases the weight significantly
Test statistics
t=
𝐼 𝑥1 −𝑥2 𝐼
𝑆.𝐸.𝑜𝑓 (𝑥1−𝑥2)
SE of (x̅1-x̅2) =
𝑆𝐷1
𝑛1
2
+
𝑆𝐷2
𝑛2
2
=
8.22
9
2
+
8.562
7
=4.25
JDP-CM-SMBT 5

6. t =
𝐼 𝑥1 −𝑥2 𝐼
𝑆.𝐸.𝑜𝑓 (𝑥1−𝑥2)
=
𝐼56 −45 𝐼
4.25
=2.59
tcal = 2.59
df= (7-1)+(9-1)= 14, 5%
ttab=2.145
tcal < ttab hence Reject H0
Conclusion
There is significant difference
between mean weight of
two groups i.e. the medicine
increases the weight
significantly
JDP-CM-SMBT 6

7. Paired t-test
Paired observation for same individuals( n1=n2=n)
Used to compare the effect of two drugs, given to same
individuals.
If there are n number of paired observation in the data set (x=
before, y=after)
 To test whether there is no difference between the mean of
before and after the observations.
Null hypothesis, Ho: D̅=0 i.e. there is no significant difference
between the means before and after the observations.
(Treatment is not effective in case of drug).
Alternative Hypothesis, H1: D̅ ‡ 0( treatment is effective)
JDP-CM-SMBT 7

8. Test Procedure:-
a) Let D=(x-y) be the difference between each set of paired
observation before and after the experiment.
b) Calculate mean of the difference D̅ =
Σ𝐷
𝑛
c) Calculate SD of difference SD=
Σ 𝐷−𝐷 2
𝑛−1
d) Test statistics, t=
𝐷
𝑆.𝐸𝑜𝑓 (𝐷)
,
𝑆. 𝐸𝑜𝑓 (𝐷) =
𝑆𝐷
𝑛
df=n-1.
a) Decision rule,
if ι t ι < tab t then accept Ho otherwise reject it.
JDP-CM-SMBT 8

9. 2) Systolic blood pressure of 6 hypertensive patients were 183, 179,165,
190,175 and 180 mm of Hg. After administration of a particular drug for 1
week the BP’s were 185, 175, 150, 180, 172 and 170 mm of Hg respectively.
Test whether drug is effective or not.
Ans:-
Null hypothesis,
Ho: D̅=0 i.e. Drug is not effective.
H1: Drug is effective
Let us calculate D and SD
D̅ =
Σ𝐷
𝑛
=40/5 =6.67
SD=
Σ 𝐷−𝐷 2
𝑛−1
=
187.33
5
=6.12
Test statistics,
t=
𝐷
𝑆.𝐸𝑜𝑓 (𝐷)
,
X=Before Y=After D= X-Y 𝑫 − 𝑫 𝟐
183 185 -2 75.17
179 175 4 7.13
165 150 15 69.39
190 180 10 11.09
175 172 3 13.47
180 170 10 11.09
∑ 40 187.33
JDP-CM-SMBT 9

10. 𝑆. 𝐸𝑜𝑓 (𝐷) =
𝑆𝐷
𝑛
=
6.12
5
= 2.74
t=
𝐷
𝑆.𝐸𝑜𝑓 (𝐷)
=
6.67
2.74
= 2.43
tdf=5,0.05 =2.571
Here tcal < ttab accept H0
Drug is effective.
JDP-CM-SMBT 10

11. Thank You
JDP-CM-SMBT 11