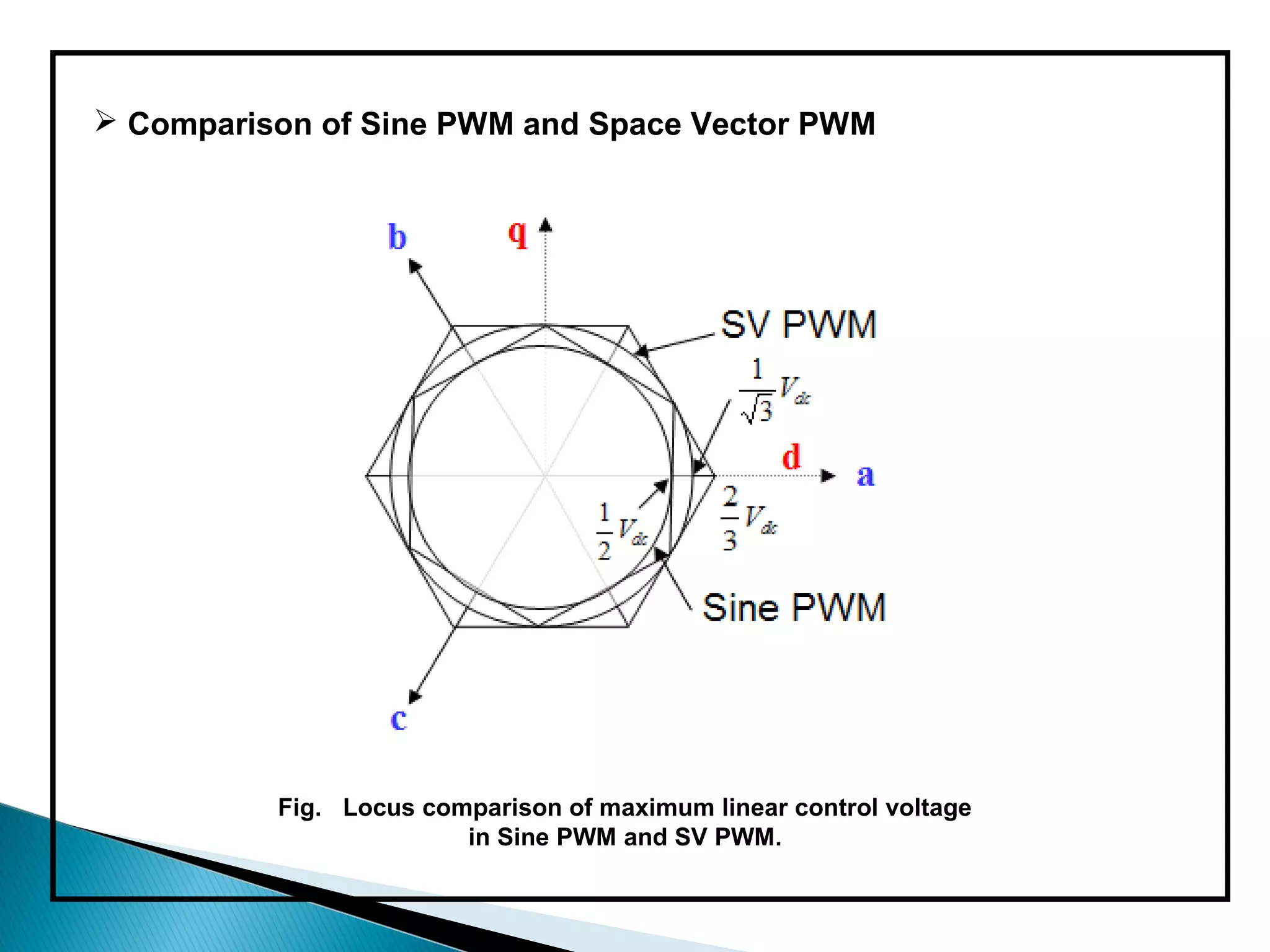
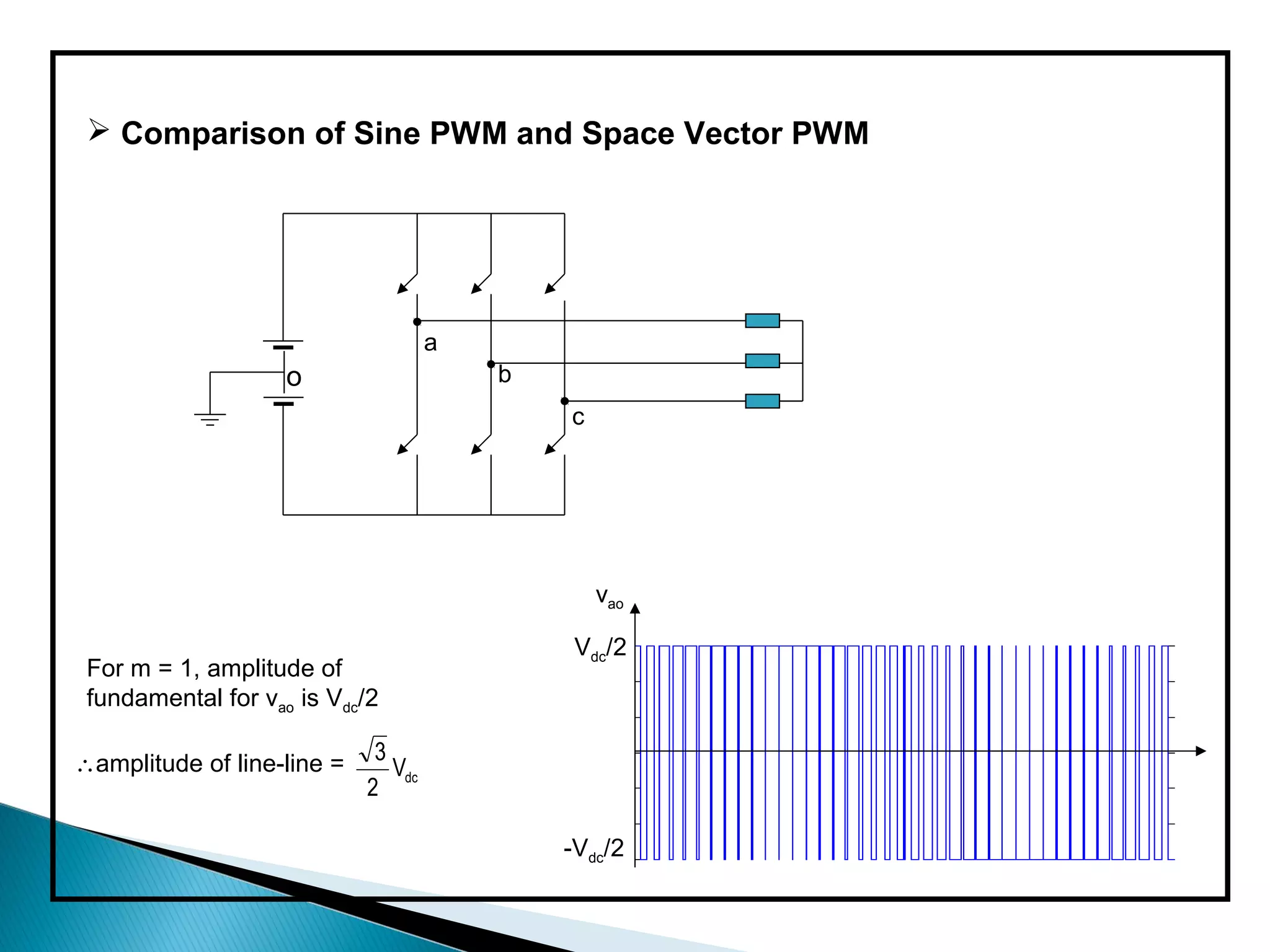
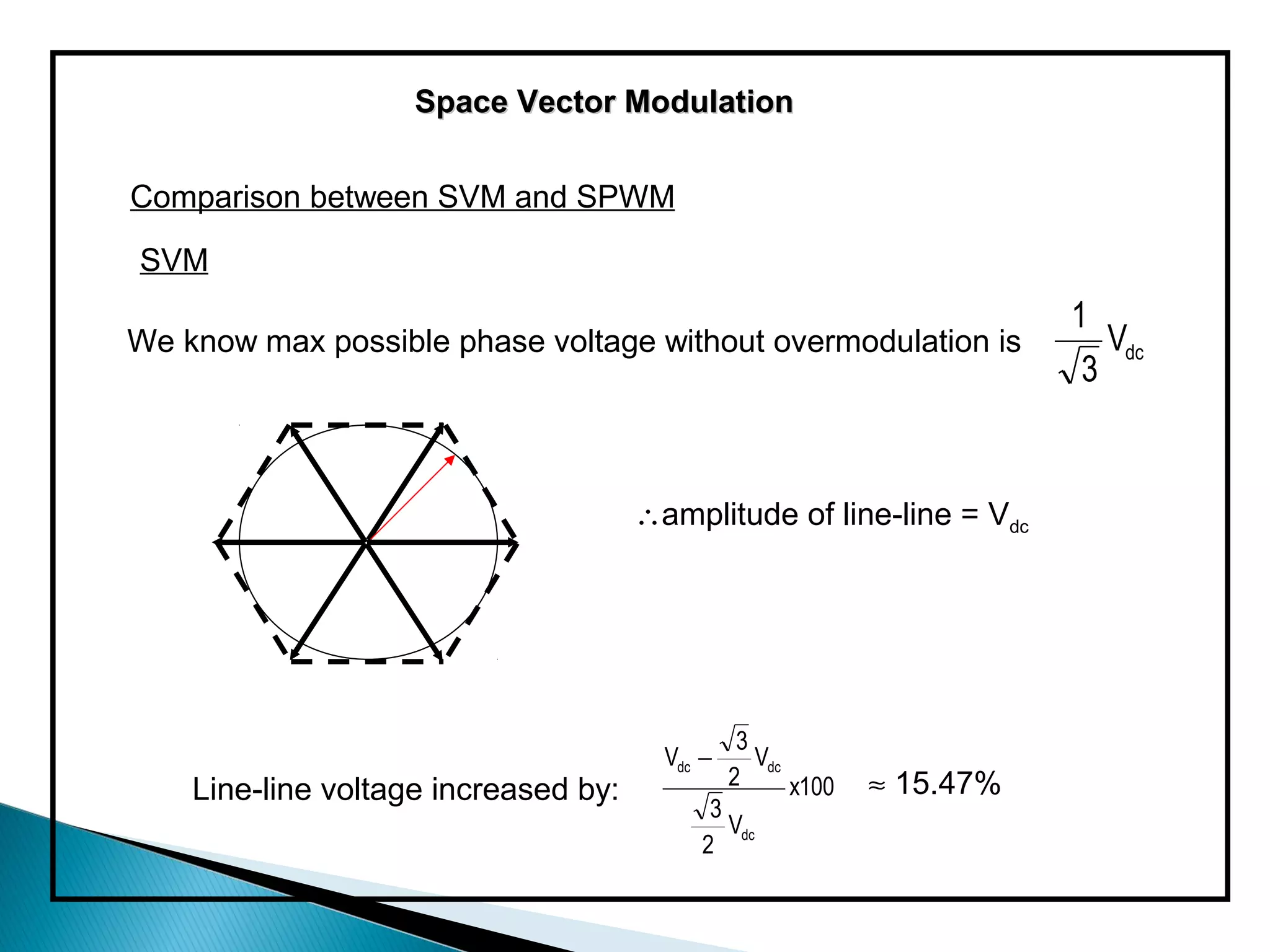
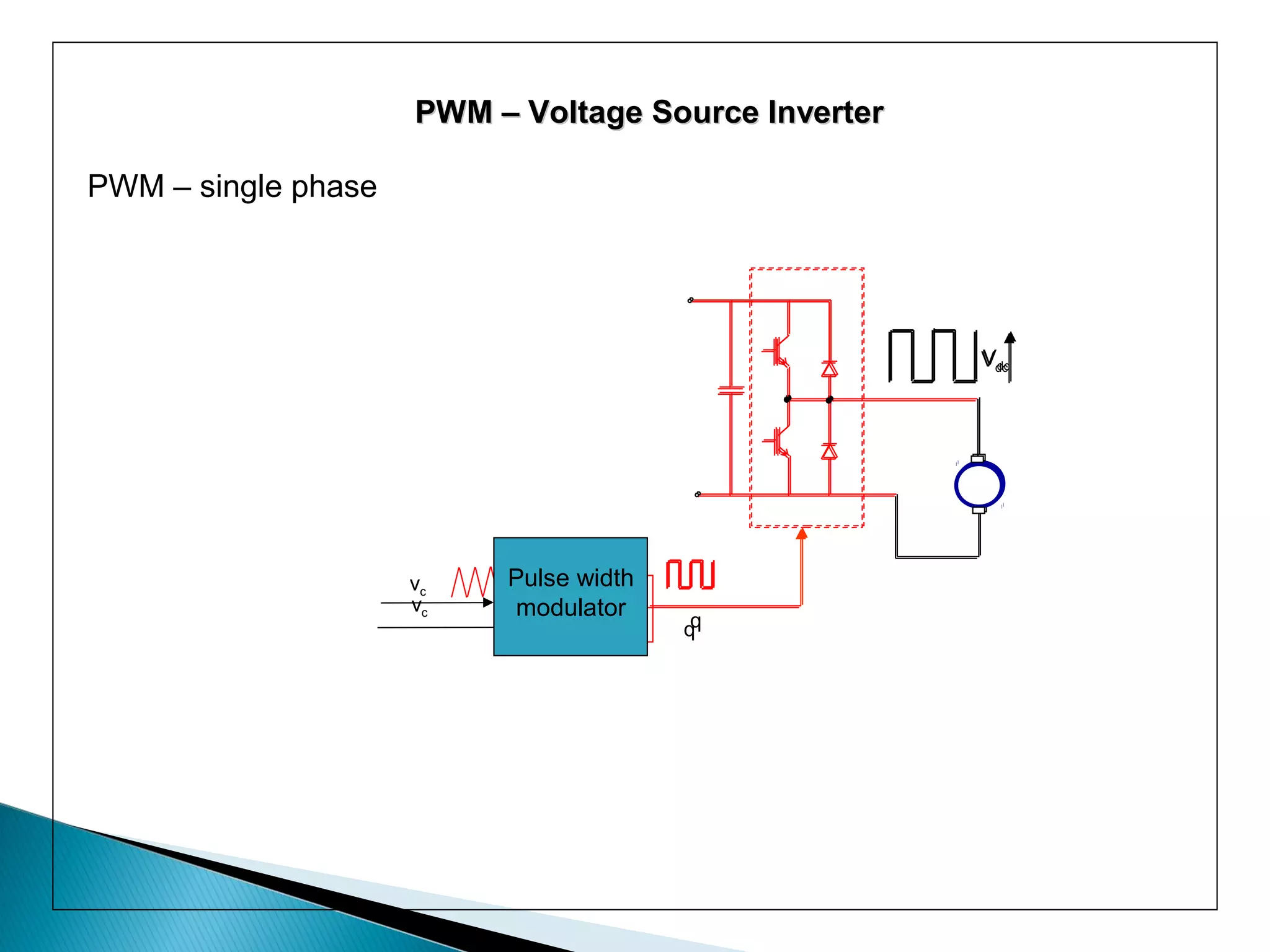
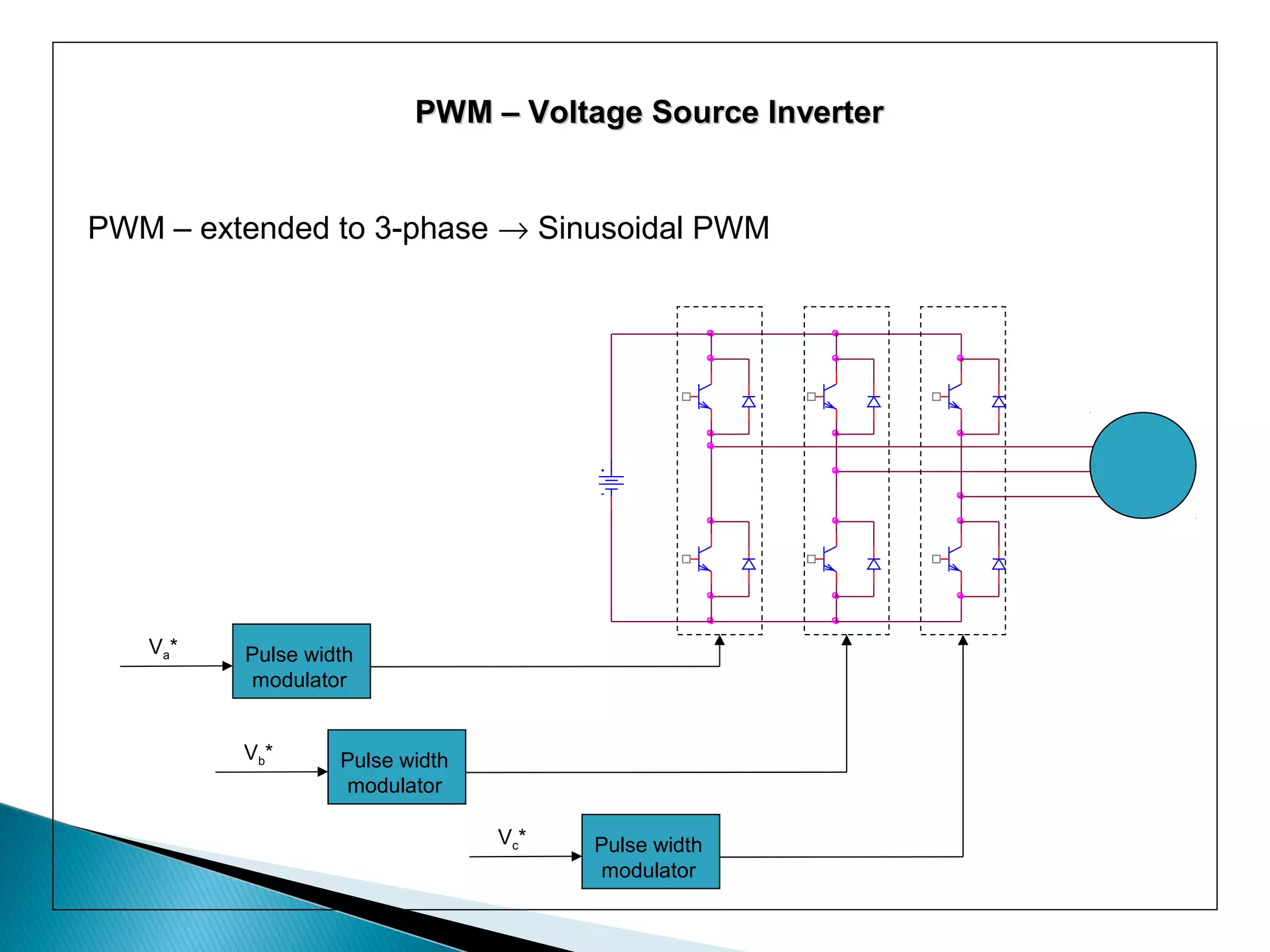
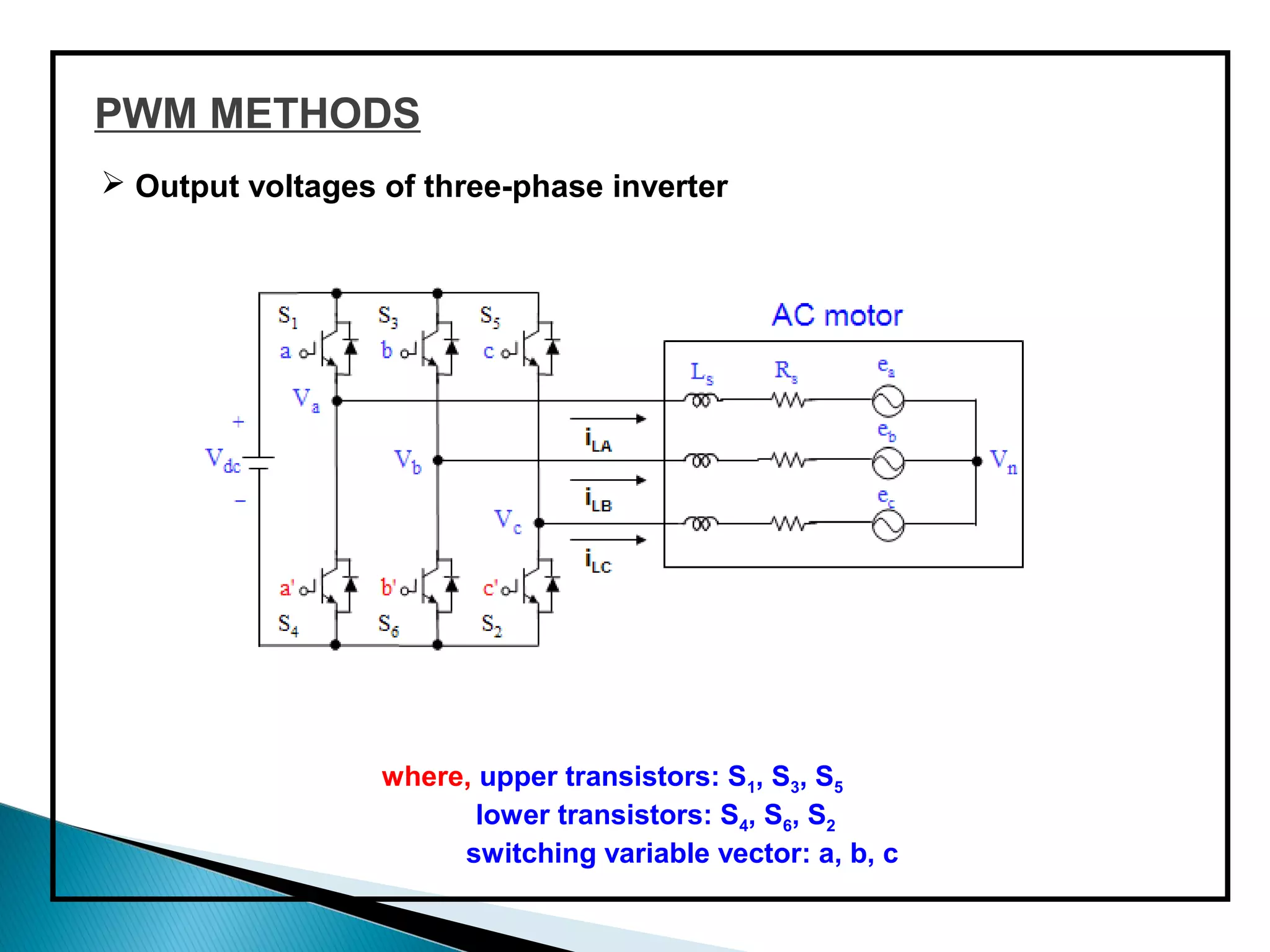
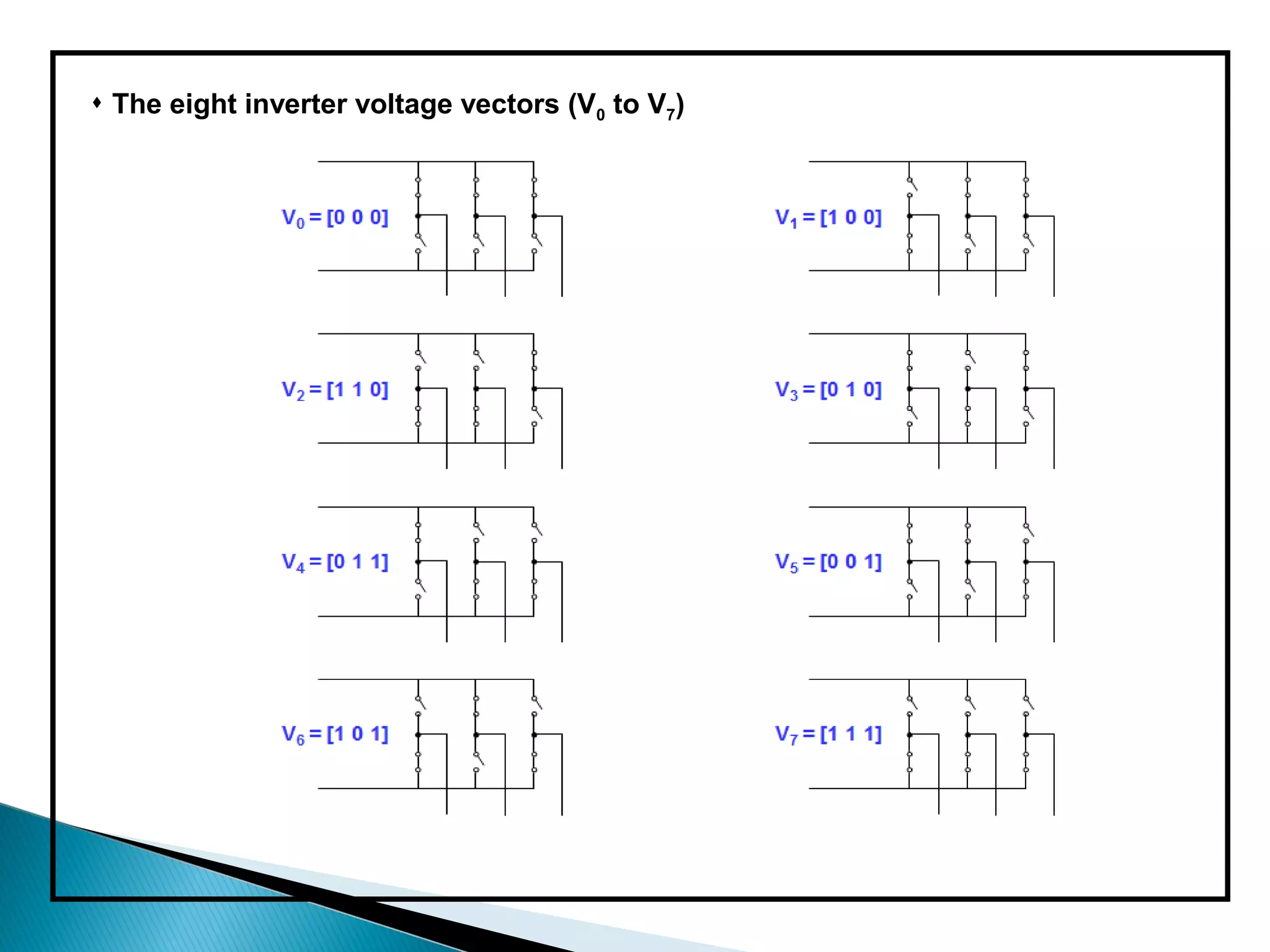
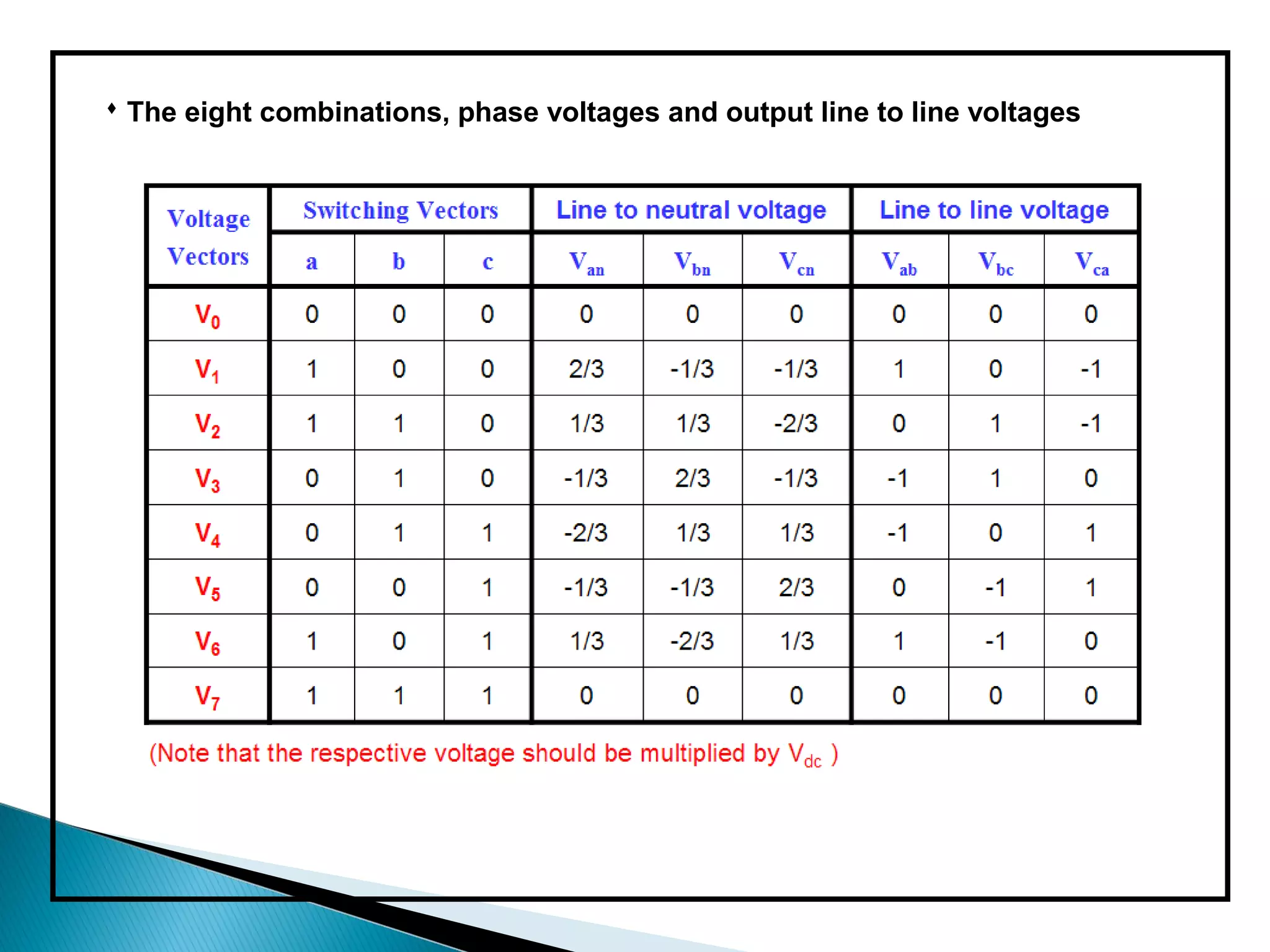
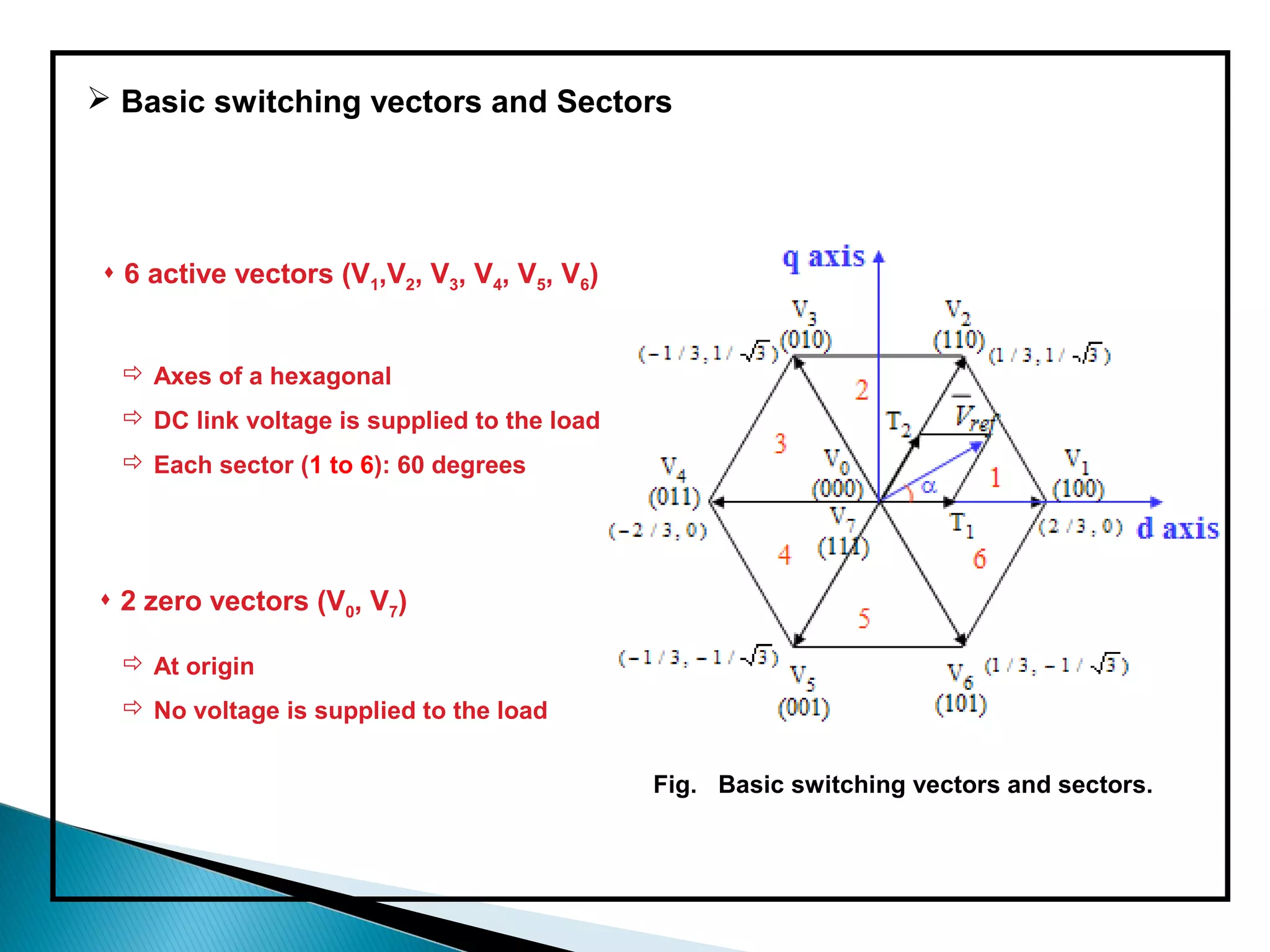
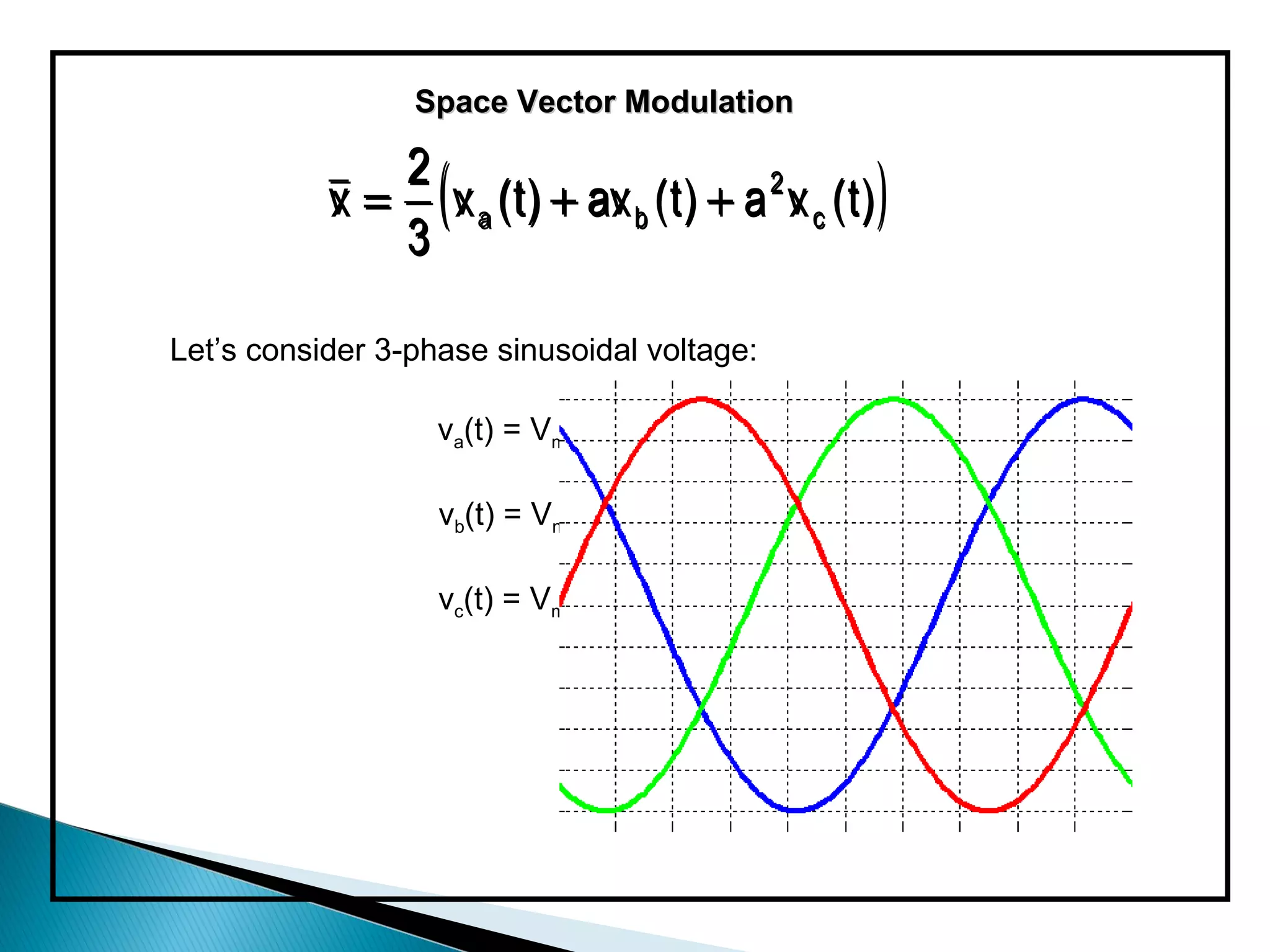
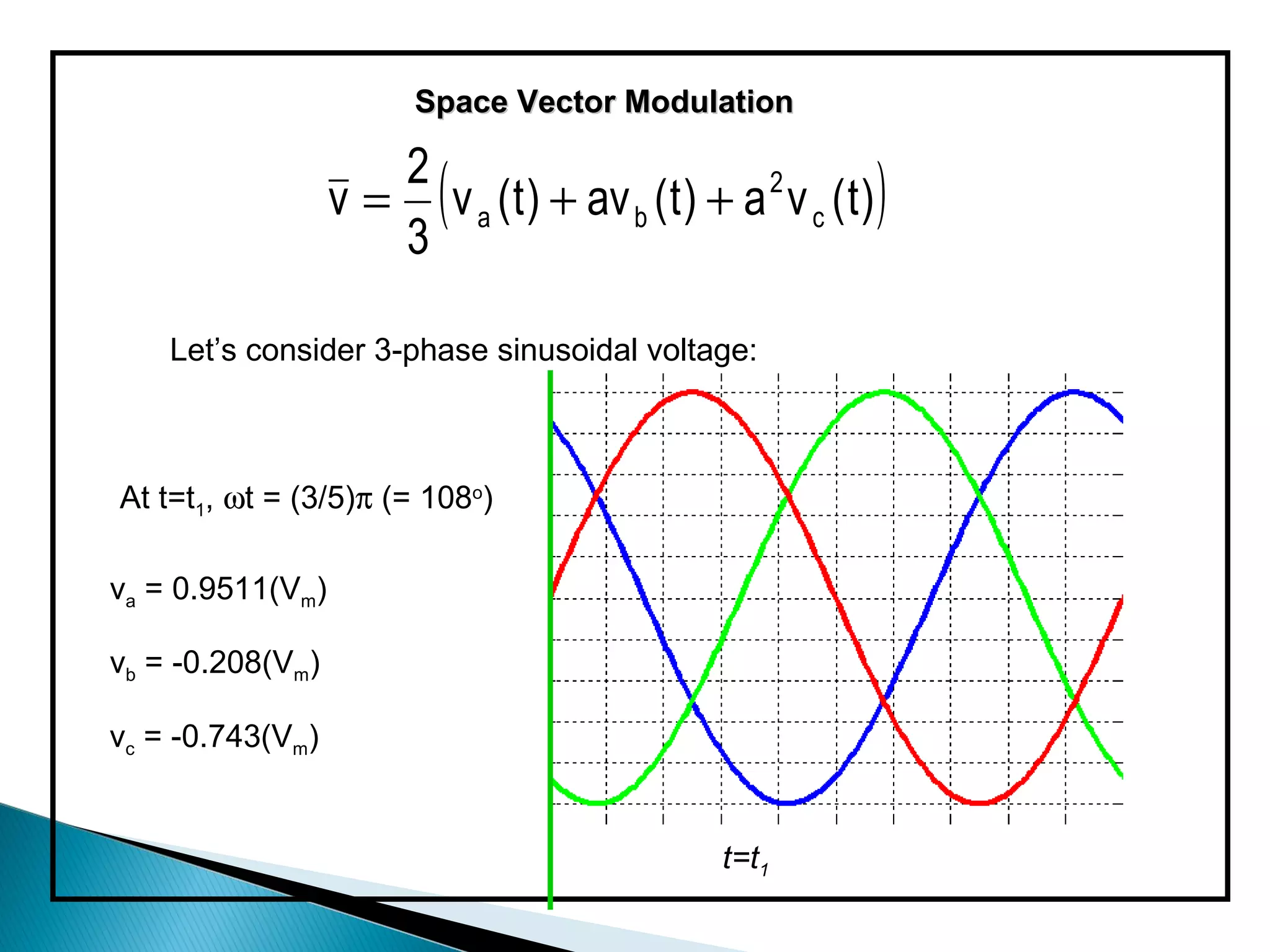
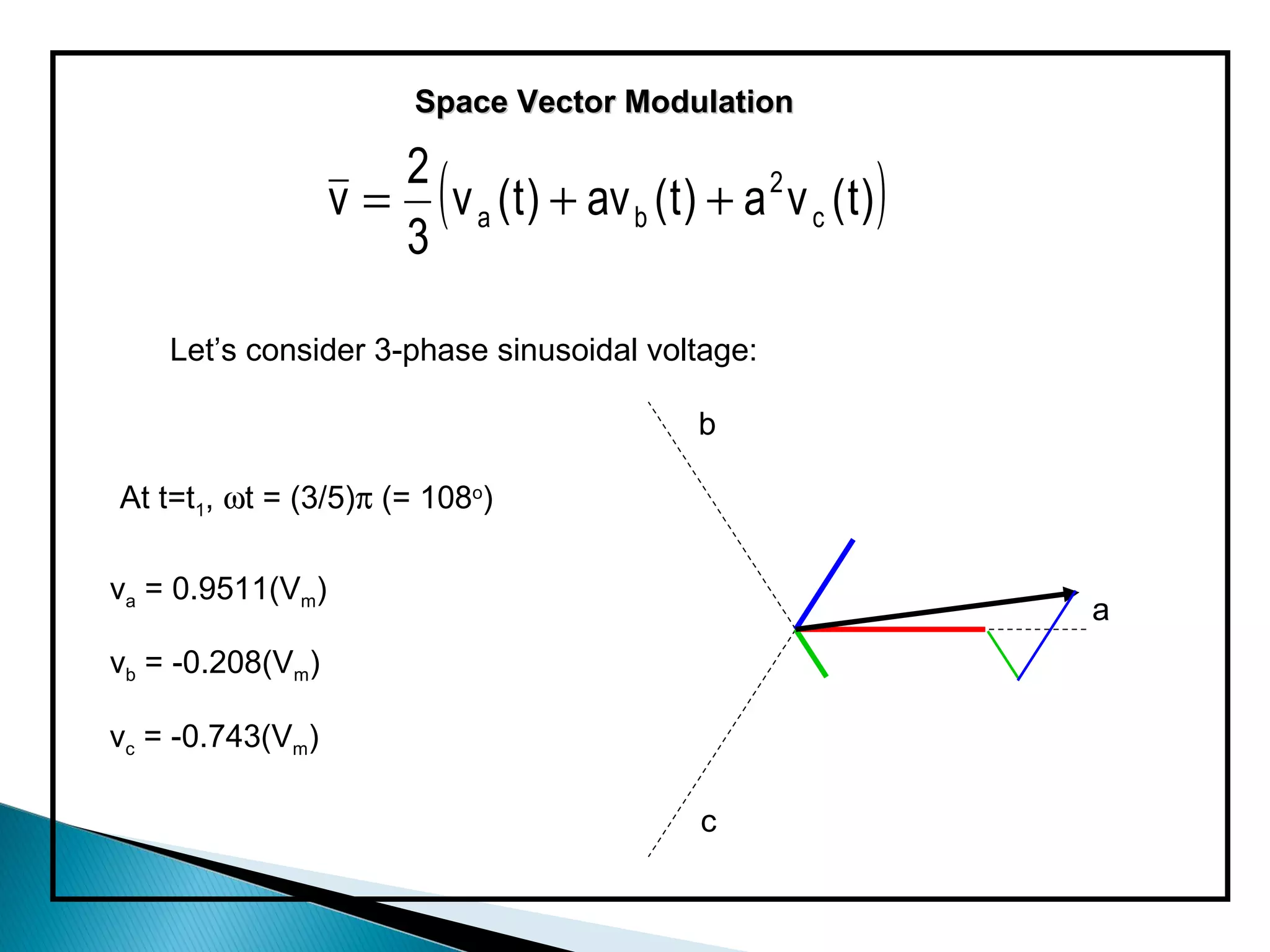
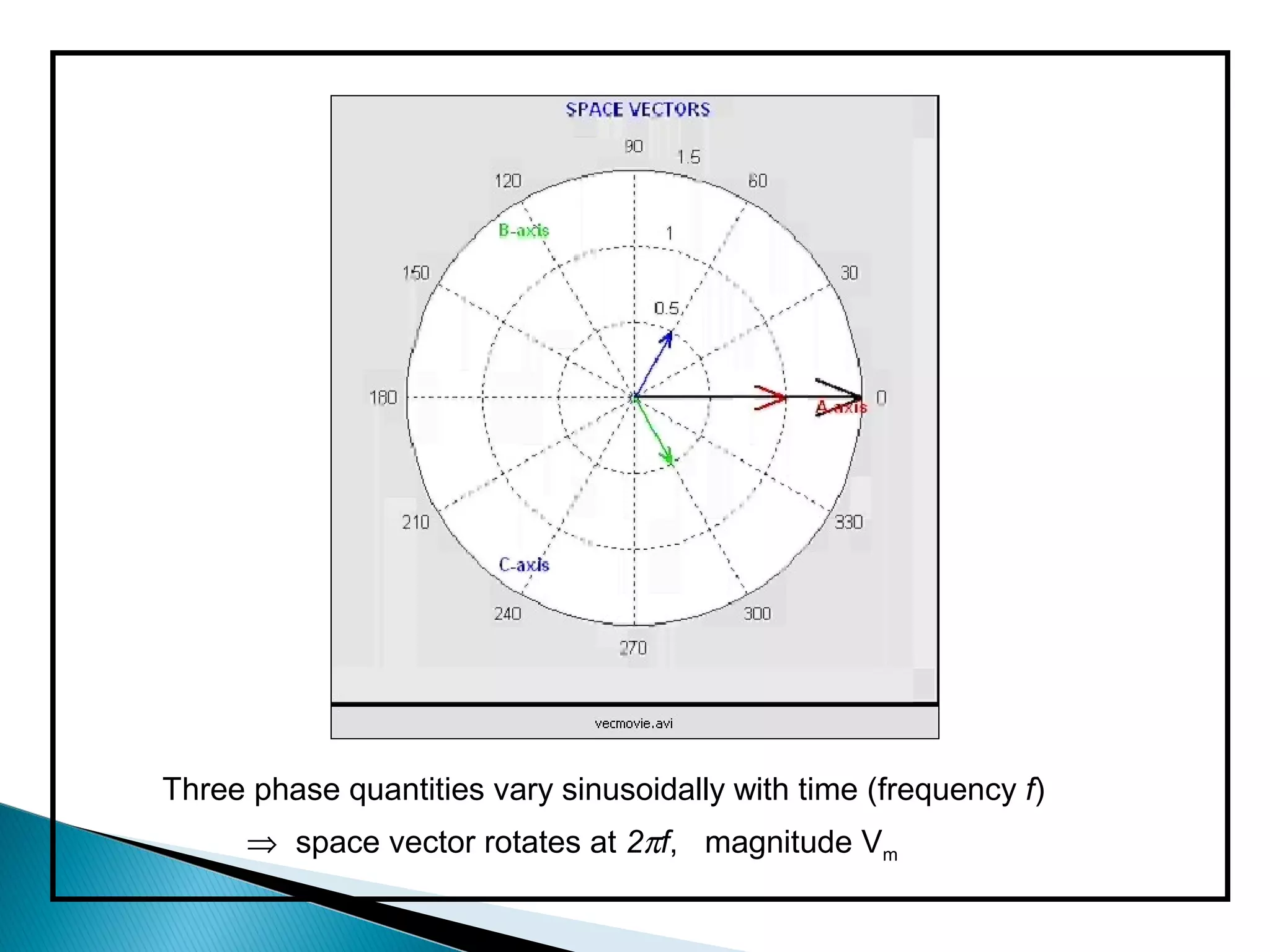
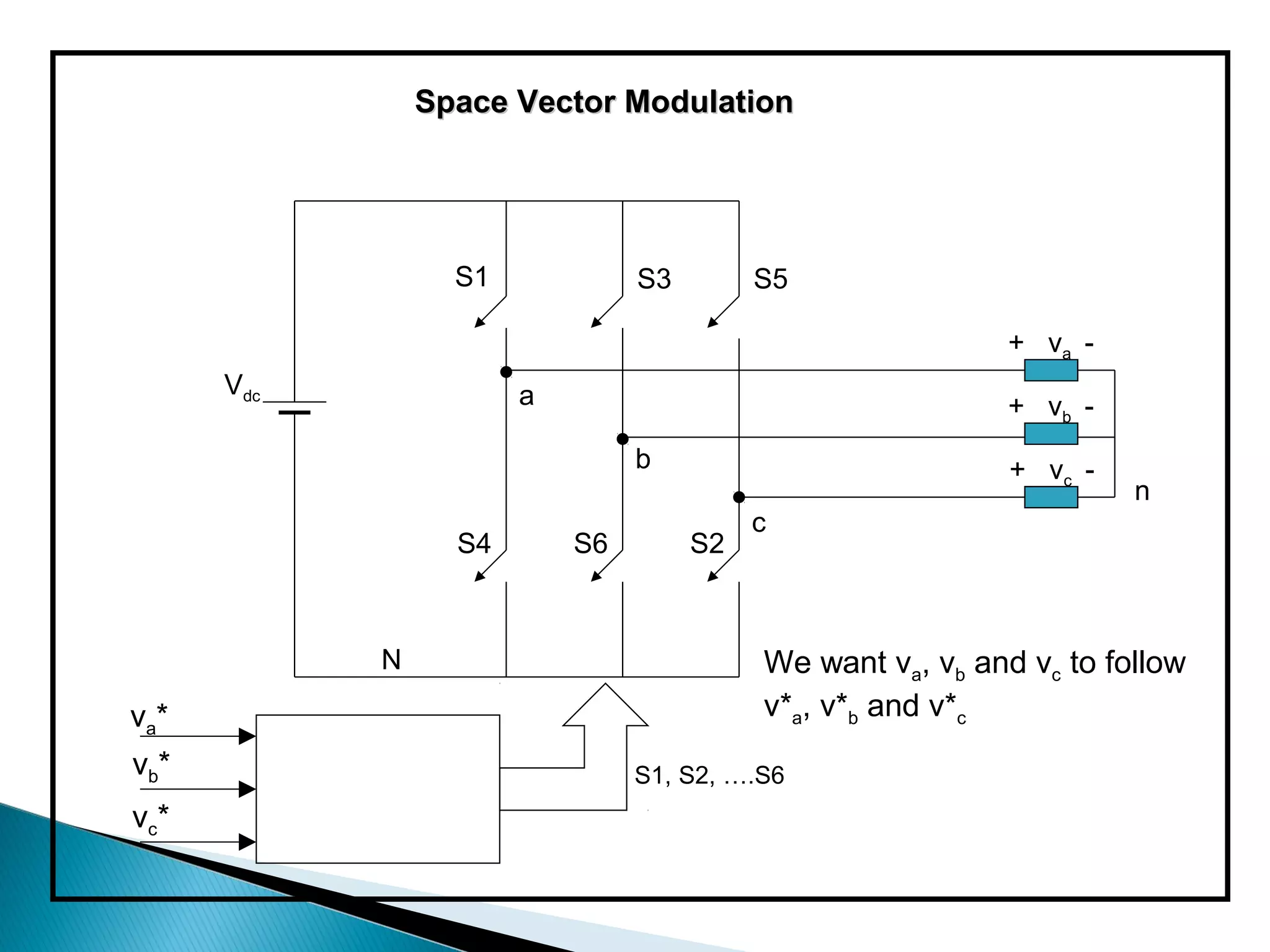
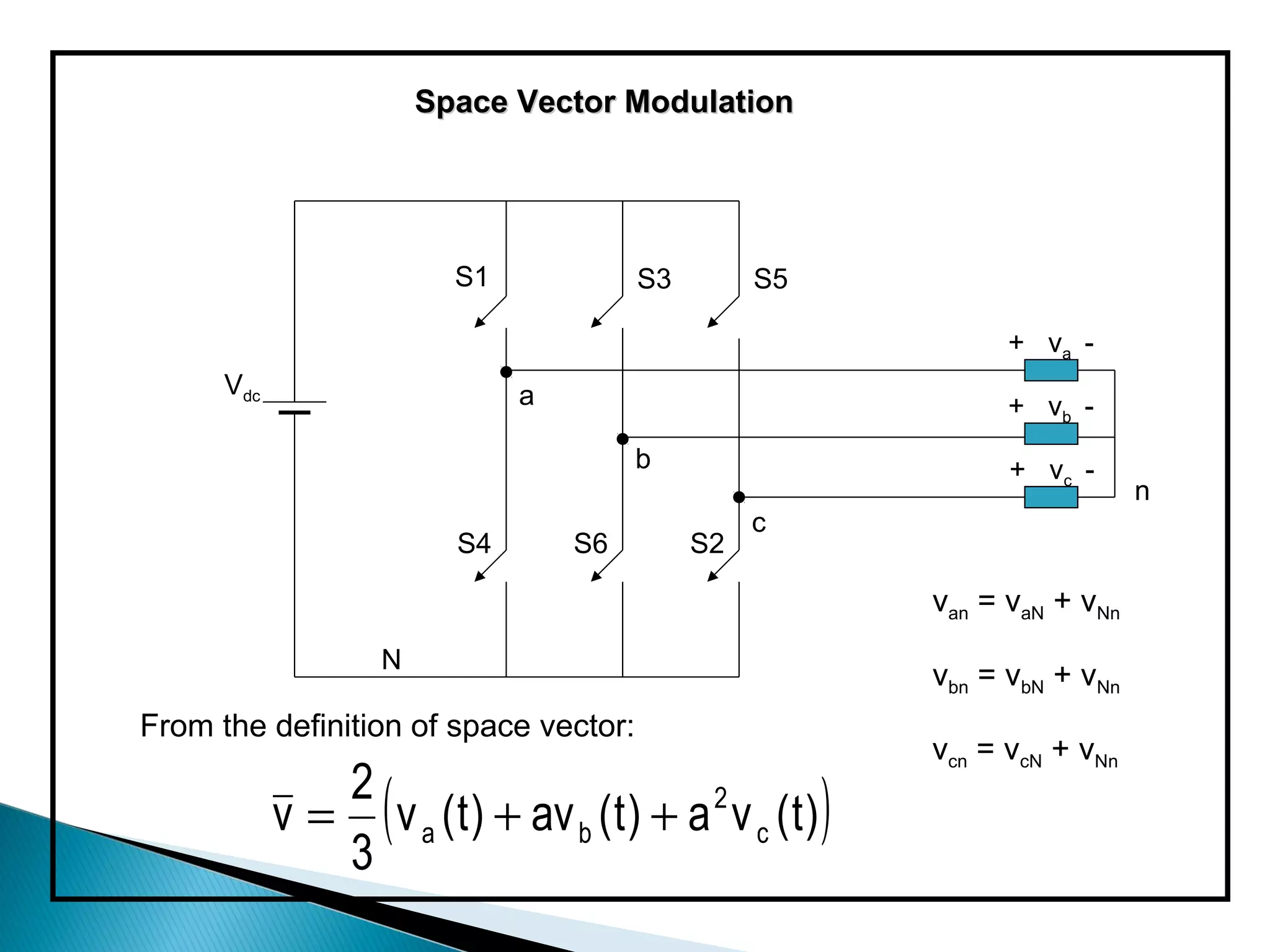
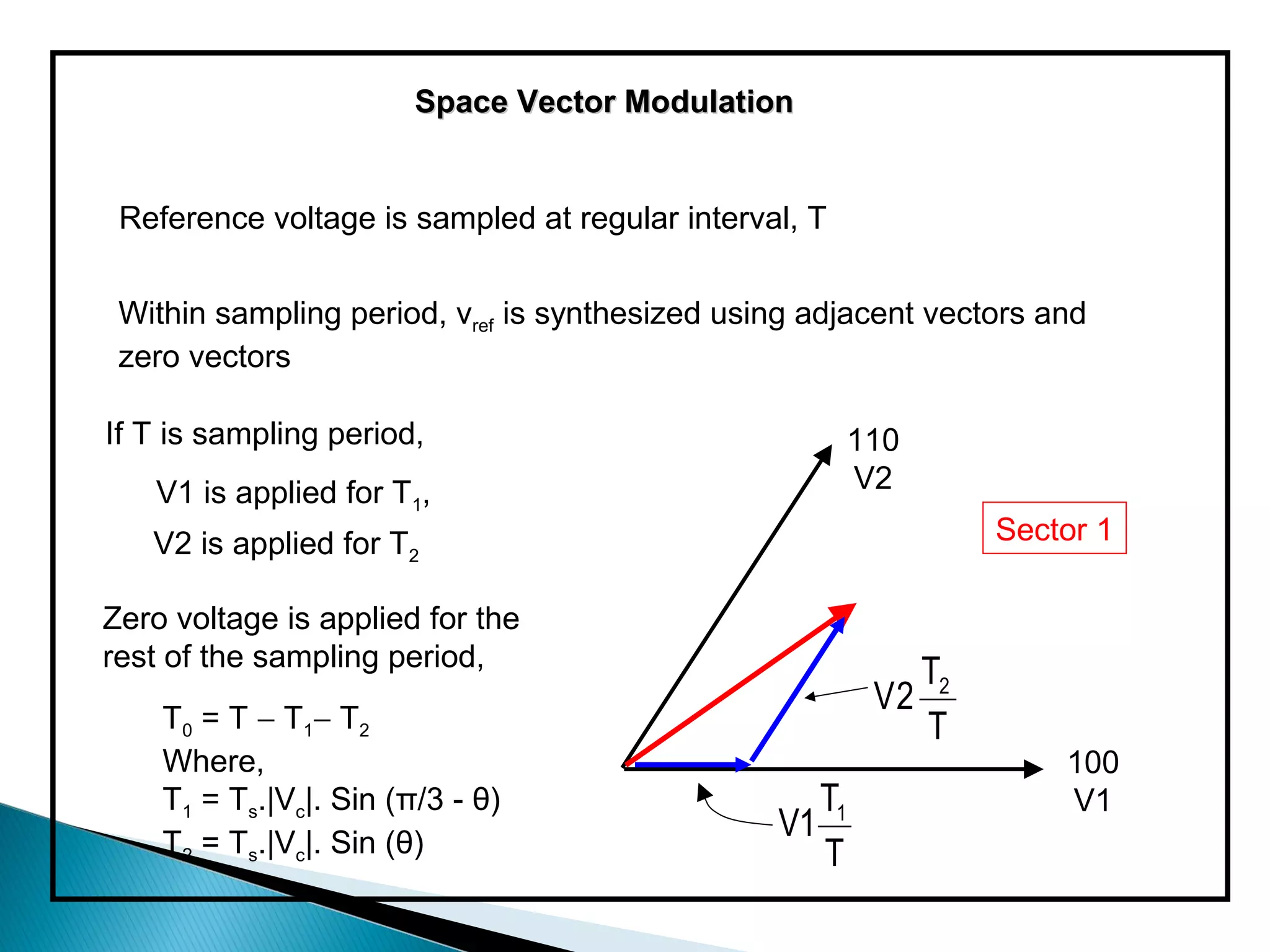
The document discusses space vector pulse width modulation (SVM) techniques for three-phase voltage source inverters. It explains the principles of SVM including coordinate transformation, reference voltage approximation using switching vectors, and calculation of switching times. Key advantages of SVM over sinusoidal PWM are more efficient voltage utilization and less output harmonic distortion. SVM allows the reference vector locus to reach the maximum circle compared to the inner circle for sinusoidal PWM, improving voltage utilization by around 15%.

1. Submitted by,
Soumya Ranjan Pradhan

2. Introduction:
 Principle of Space Vector PWM
 Treats the sinusoidal voltage as a constant amplitude vector rotating
at constant frequency.
 Coordinate Transformation ( abc reference frame to the stationary d-q frame)
: A three-phase voltage vector is transformed into a vector in the stationary d-q coordinate
frame which represents the spatial vector sum of the three-phase voltage.
 This PWM technique approximates the reference voltage Vref by a combination
of the eight switching patterns (V0 to V7).
 The vectors (V1 to V6) divide the plane into six sectors (each sector: 60 degrees).
 Vref is generated by two adjacent non-zero vectors and two zero vectors.

3. PWM – Voltage Source Inverter
Open loop voltage control
VSI AC
vref PWM
motor
Closed loop current-control
AC
iref PWM VSI motor
if/back

4. PWM – Voltage Source Inverter
PWM – single phase
Vdc
dc
vc vPulse width
tri
vc modulator
qq

5. PWM – Voltage Source Inverter
PWM – extended to 3-phase → Sinusoidal PWM
Va* Pulse width
modulator
Vb* Pulse width
modulator
Vc* Pulse width
modulator

6. PWM METHODS
 Output voltages of three-phase inverter
where, upper transistors: S1, S3, S5
lower transistors: S4, S6, S2
switching variable vector: a, b, c

7.  The eight inverter voltage vectors (V0 to V7)

8.  The eight combinations, phase voltages and output line to line voltages

9.  Basic switching vectors and Sectors
 6 active vectors (V1,V2, V3, V4, V5, V6)
 Axes of a hexagonal
 DC link voltage is supplied to the load
 Each sector (1 to 6): 60 degrees
 2 zero vectors (V0, V7)
 At origin
 No voltage is supplied to the load
Fig. Basic switching vectors and sectors.

10. Space Vector Modulation
Definition:
Space vector representation of a three-phase quantities xa(t), xb(t) and
xc(t) with space distribution of 120o apart is given by:
x = ( x a ( t ) + ax b ( t ) + a 2 x c ( t ) )
2
3
a = ej2π/3 = cos(2π/3) + jsin(2π/3)
a2 = ej4π/3 = cos(4π/3) + jsin(4π/3)
x – can be a voltage, current or flux and does not necessarily has to be sinusoidal

11. Space Vector Modulation
v = ( v a ( t ) + av b ( t ) + a 2 v c ( t ) )
2
x x ax x
3
Let’s consider 3-phase sinusoidal voltage:
va(t) = Vmsin(ωt)
vb(t) = Vmsin(ωt - 120o)
vc(t) = Vmsin(ωt + 120o)

12. Space Vector Modulation
v = ( v a ( t ) + av b ( t ) + a 2 v c ( t ) )
2
3
Let’s consider 3-phase sinusoidal voltage:
At t=t1, ωt = (3/5)π (= 108o)
va = 0.9511(Vm)
vb = -0.208(Vm)
vc = -0.743(Vm)
t=t1

13. Space Vector Modulation
v = ( v a ( t ) + av b ( t ) + a 2 v c ( t ) )
2
3
Let’s consider 3-phase sinusoidal voltage:
b
At t=t1, ωt = (3/5)π (= 108o)
va = 0.9511(Vm)
a
vb = -0.208(Vm)
vc = -0.743(Vm)
c

14. Three phase quantities vary sinusoidally with time (frequency f)
⇒ space vector rotates at 2πf, magnitude Vm

15. Space Vector Modulation
S1 S3 S5
+ va -
Vdc a + vb -
b + vc -
n
c
S4 S6 S2
N We want va, vb and vc to follow
va* v*a, v*b and v*c
vb* S1, S2, ….S6
vc*

16. Space Vector Modulation
S1 S3 S5
+ va -
Vdc a + vb -
b + vc -
n
c
S4 S6 S2
van = vaN + vNn
N
vbn = vbN + vNn
From the definition of space vector:
vcn = vcN + vNn
v = ( v a ( t ) + av b ( t ) + a 2 v c ( t ) )
2
3

17. Space Vector Modulation
=0
2
(
v = v aN + av bN + a 2 v cN + v Nn (1 + a + a 2 )
3
)
vaN = VdcSa, vaN = VdcSb, vaN = VdcSa, Sa, Sb, Sc = 1 or 0
2
(
v = Vdc S a + aS b + a 2 S c
3
)
v = ( v a ( t ) + av b ( t ) + a 2 v c ( t ) )
2
3

18. Space Vector Modulation
Sector 2
[010] V3 [110] V2
(1/√3)Vdc
Sector 3 Sector 1
[100] V1
[011] V4
(2/3)Vdc
Sector 4 2
(
v = Vdc S a + aS b + a 2 S c
3
) Sector 6
[001] V5 Sector 5 [101] V6

19. Conversion from 3 phases to 2 phases :
For Sector 1,
Three-phase line modulating signals (VC)abc = [VCaVCbVCc]T
can be represented by the represented by the complex vector
VC = [VC]αβ = [VCaVCb]T
by means of the following transformation:
VC α = 2/3 . [vCa - 0.5(vCb + vCc )]
VC β = √3/3 . (vCb - vCc)

20. Space Vector Modulation
Reference voltage is sampled at regular interval, T
Within sampling period, vref is synthesized using adjacent vectors and
zero vectors
If T is sampling period, 110
V1 is applied for T1, V2
V2 is applied for T2 Sector 1
Zero voltage is applied for the
rest of the sampling period,
T2
V2
T 0 = T − T 1− T 2 T
Where, 100
T1 = Ts.|Vc|. Sin (π/3 - θ) T1 V1
T2 = Ts.|Vc|. Sin (θ)
V1
T

21. Space Vector Modulation
Reference voltage is sampled at regular interval, T
Within sampling period, vref is synthesized using adjacent vectors and
zero vectors
T0/2 T1 T2 T0/2
V0 V1 V2 V7
If T is sampling period,
V1 is applied for T1, va
V2 is applied for T2
vb
Zero voltage is applied for the
rest of the sampling period, vc
T0 = T − T1− T2
T T
Vref is sampled Vref is sampled

22. Space Vector Modulation
How do we calculate T1, T2, T0 and T7?
They are calculated based on volt-second integral of vref
1 T 1  To T1 T2 T7

∫
T 0 T 0 ∫ 0 ∫ 0 ∫
v ref dt =  v 0 dt + v 1dt + v 2 dt + v 7 dt 
0  ∫
v ref ⋅ T = v o ⋅ To + v 1 ⋅ T1 + v 2 ⋅ T2 + v 7 ⋅ T7
2 2
v ref ⋅ T = To ⋅ 0 + Vd ⋅ T1 + Vd (cos 60o + j sin 60o )T2 + T7 ⋅ 0
3 3
2 2
v ref ⋅ T = Vd ⋅ T1 + Vd (cos 60o + j sin 60o )T2
3 3

23. Space Vector Modulation
q T = T1 + T2 + T0,7
110
V2
Sector 1
v ref ⋅ = v ref ( cos α − j sin α )
α
100
2 2 V1 d
v ref ⋅ T = Vd ⋅ T1 + Vd (cos 60o + j sin 60 )T2
o
3 3

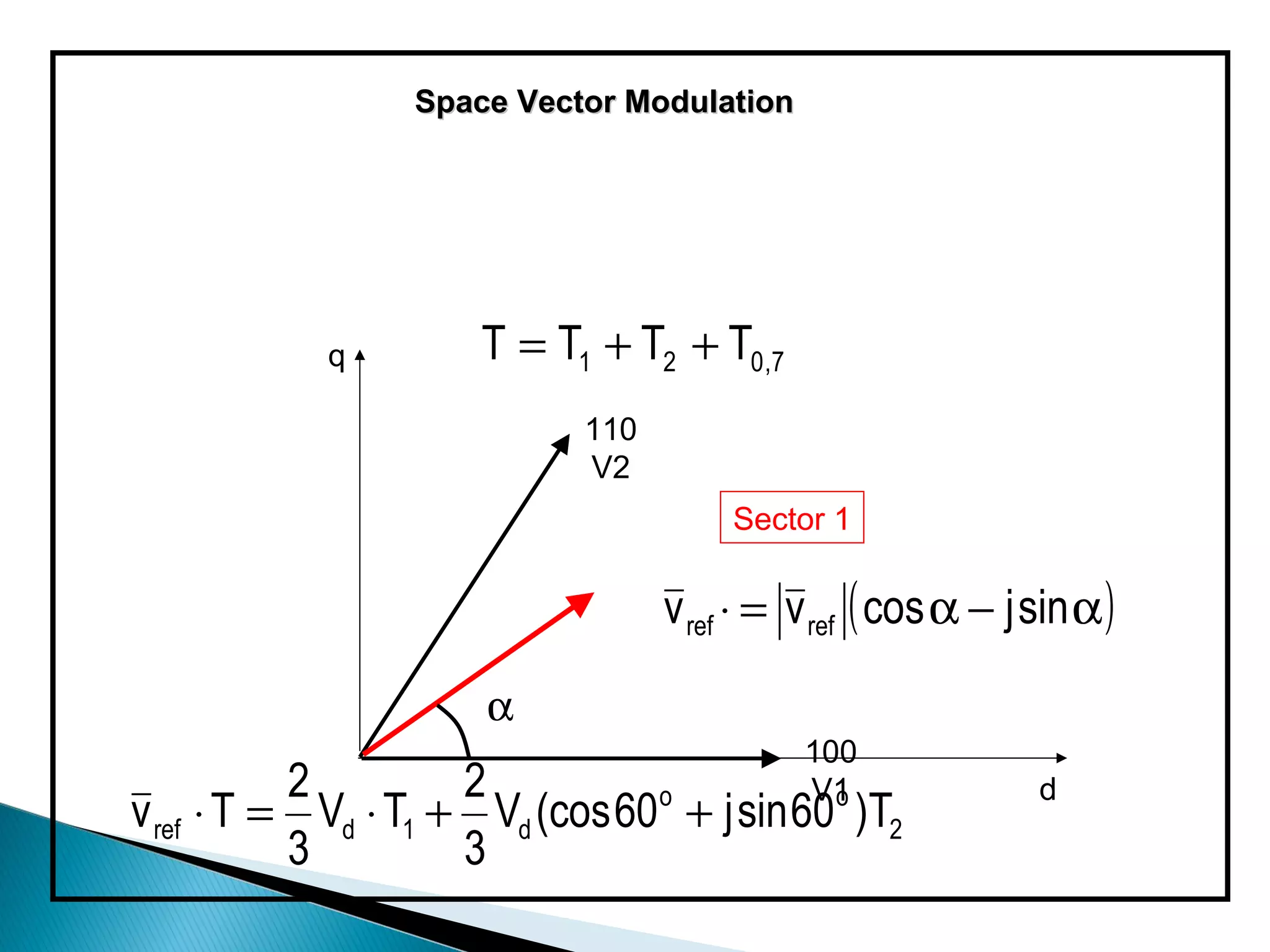
24. Space Vector Modulation
2 2
v ref ⋅ T = Vd ⋅ T1 + Vd (cos 60o + j sin 60o )T2
3 3
2 1 1
T v ref cos α = Vd T1 + Vd T2 T v ref sin α = Vd T2
3 3 3
Solving for T1, T2 and T0,7 gives:
T1= 3/2 m[ (T/√3) cos α - (1/3)T sin α ]
T2= mT sin α
where,
M= Vref/ (Vd/ √3)

25.  Comparison of Sine PWM and Space Vector PWM
Fig. Locus comparison of maximum linear control voltage
in Sine PWM and SV PWM.

26.  Comparison of Sine PWM and Space Vector PWM
a
o b
c
vao
Vdc/2
For m = 1, amplitude of
fundamental for vao is Vdc/2
∴amplitude of line-line = 3
Vdc
2
-Vdc/2

27.  Comparison of Sine PWM and Space Vector PWM
 Space Vector PWM generates less harmonic distortion
in the output voltage or currents in comparison with sine PWM
 Space Vector PWM provides more efficient use of supply voltage
in comparison with sine PWM
 Sine PWM
: Locus of the reference vector is the inside of a circle with radius of 1/2 V dc
 Space Vector PWM
: Locus of the reference vector is the inside of a circle with radius of 1/√3 Vdc
∴ Voltage Utilization: Space Vector PWM = 2/√3 or (1.1547) times
of Sine PWM, i.e. 15.47% more utilization of voltage.

28. Space Vector Modulation
Comparison between SVM and SPWM
SVM
1
We know max possible phase voltage without overmodulation is Vdc
3
∴amplitude of line-line = Vdc
3
Vdc − Vdc
2 ≈ 15.47%
Line-line voltage increased by: x100
3
Vdc
2

29. 1. Power Electronics: Circuits, Devices and Applications by M. H. Rashid, 3rd edition,
Pearson
2. Power Electronics: Converters, Applications and Devices by Mohan, Undeland and
Robbins, Wiley student edition
3. Power Electronics Handbook: M.H. Rashid, Web edition
4. Modern Power Electronics And Ac Drives: B.K. Bose
5. Extended Report on AC drive control, IEEE : Issa Batarseh
6. Space vector modulation: Google, Wikipedia ; for figures.