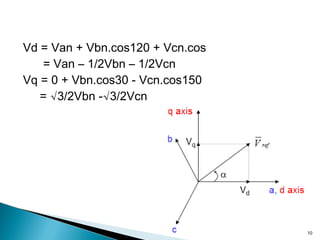
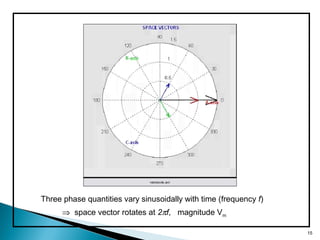
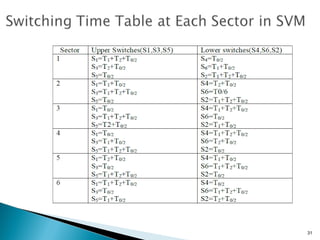
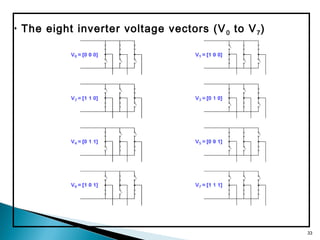
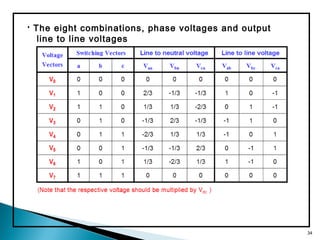
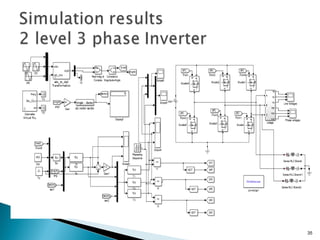
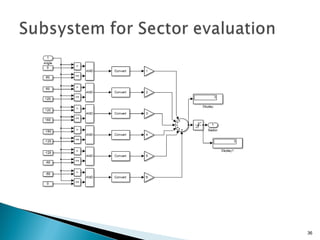
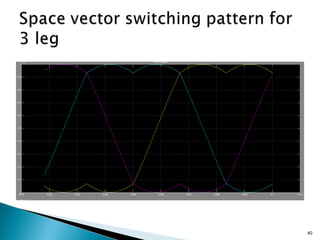
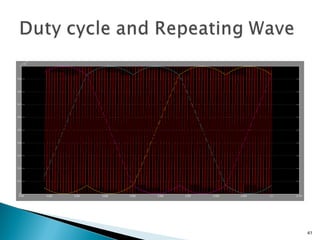
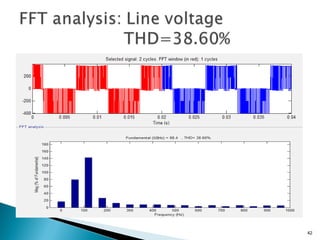
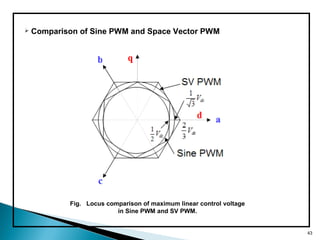
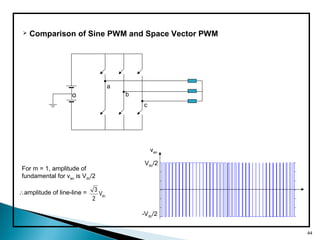
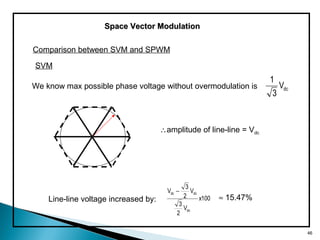
This document discusses space vector pulse width modulation (SVM) for three-phase voltage source inverters. It begins by introducing SVM and its benefits over other PWM techniques, such as reduced total harmonic distortion. It then provides details on how SVM works, including transforming a three-phase reference signal to a rotating vector in the d-q reference frame. The document explains the eight possible switching states, sectors, and how to calculate switching times to synthesize the reference signal using adjacent active vectors and zero vectors. It concludes by comparing SVM to sinusoidal PWM, showing SVM offers better voltage utilization and harmonic performance.

1. 1

2.  Amey Patil (BT11EEE05)
 Amey Khot (BT11EEE06)
 Charudatt Awaghate (BT11EEE18)
 Srikant Pillai (BT11EEE51)
 Purushotam Kumar (BT11EEE53)
2

3.  The space vector PWM (SVM) method is an advanced
computation-intensive PWM method and is possibly the
best method among the all PWM techniques for variable-
frequency drive application. Because of its superior
performance characteristics, it has been finding wide
spread application in recent years.
 There are various variations of SVM that result in
different quality and computational requirements.
 One major benefit is in the reduction of total harmonic
distortion (THD) created by the rapid switching inherent
to this PWM algorithm.
3

4. vtri
Vdc
q
vc
q
Vdc
Pulse width
modulator
vc
PWM – single phase
PWM – Voltage Source InverterPWM – Voltage Source Inverter
4

5. PWM – extended to 3-phase → Sinusoidal PWM
Pulse width
modulator
Va*
Pulse width
modulator
Vb*
Pulse width
modulator
Vc*
PWM – Voltage Source InverterPWM – Voltage Source Inverter
5

6.  Output voltages of three-phase inverter
Simple 3 phase Inverter
Fig1
where, upper transistors: S1, S3, S5
lower transistors: S4, S6, S2
switching variable vector: a, b, c
6

7.  Treats the sinusoidal voltage as a constant amplitude vector
rotating at constant frequency.
 Coordinate Transformation ( abc reference frame to the
stationary d-q frame)
A three-phase voltage vector is transformed into a vector in the stationary d-q
coordinate frame which represents the spatial vector sum of the three-phase
voltage.
 This PWM technique approximates the reference voltage Vref
by a combination of the eight switching patterns (V0 to V7)
7

8. + vc -
+ vb -
+ va -
n
N
Vdc a
b
c
From the definition of space vector:
( ))t(va)t(av)t(v
3
2
v c
2
ba ++=
S1
S2
S3
S4
S5
S6
• The vectors (V1 to V6) divide the plane into six sectors
(each sector: 60 degrees).
• Vref is generated by two adjacent non-zero vectors
and two zero vectors.
van = vaN + vNn
vbn = vbN + vNn
vcn = vcN + vNn
8

9. Let’s consider 3-phase sinusoidal voltage:
va(t) = Vmsin(ωt)
vb(t) = Vmsin(ωt - 120o
)
vc(t) = Vmsin(ωt + 120o
)
9

10. Vd = Van + Vbn.cos120 + Vcn.cos
= Van – 1/2Vbn – 1/2Vcn
Vq = 0 + Vbn.cos30 - Vcn.cos150
= √3/2Vbn -√3/2Vcn
10

11.  The circuit model of a typical three-phase voltage source
PWM inverter is shown in Fig.2
 S1 to S6 are the six power switches that shape the
output, which are controlled by the switching variables a,
a’, b, b’, c and c’.
 When an upper transistor is switched on, i.e., when a, b
or c is 1, the corresponding lower transistor is switched
off, i.e., the corresponding a′, b′ or c’ is 0.
 Therefore, the on and off states of the upper transistors
S1, S3 and S5 can be used to determine the output
voltage.
11

12. + vc -
+ vb -
+ va -
n
N
Vdc a
b
c
S1
S2
S3
S4
S5
S6
S1, S2, ….S6
va*
vb*
vc*
We want va, vb and vc to follow
v*a, v*b and v*c
Space Vector ModulationSpace Vector Modulation
Fig:2Fig:2
12

13. 13

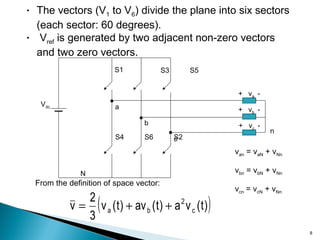
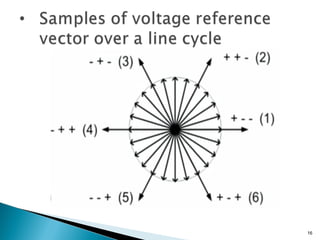
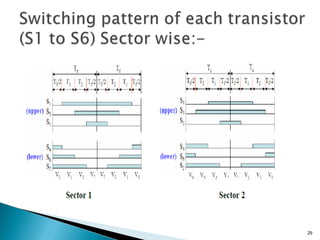
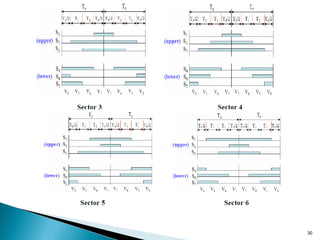
14. Sector 1Sector 3
Sector 4
Sector 5
Sector 2
Sector 6
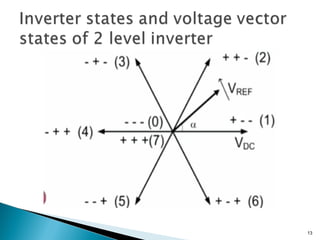
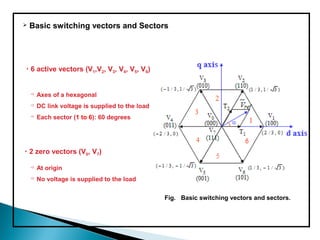
[100] V1
[110] V2[010] V3
[011] V4
[001] V5 [101] V6
(2/3)Vdc
(1/√3)Vdc
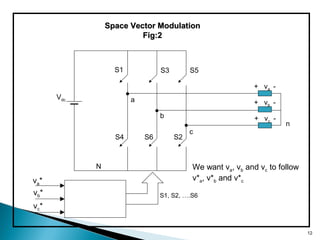
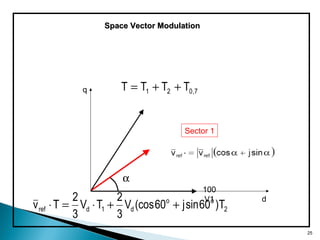
Space Vector ModulationSpace Vector Modulation
( )c
2
badc SaaSSV
3
2
v ++=
14

15. Three phase quantities vary sinusoidally with time (frequency f)
⇒ space vector rotates at 2πf, magnitude Vm
15

16. 16

17. 17

18.  Step -1 Determine Vd, Vq, Vref, and angle(alpha)
 Step -2 Determine time duration T1, T2, T0
 Step -3 Determine the switching time of each
transistor (S1 to S6)
18

19. 19

20. 20

21.  T0=T7=0.5Tz
Both zero states are
used for equal
duration
21

22. Space Vector ModulationSpace Vector Modulation
Reference voltage is sampled at regular interval, T
Within sampling period, vref is synthesized using adjacent vectors and
zero vectors
100
V1
110
V2
If T is sampling period,
V1 is applied for T1,
T
T
1V 1
V2 is applied for T2
T
T
2V 2
Zero voltage is applied for the
rest of the sampling period,
T0 = T − T1− T2
Where,
T1 = Ts.|Vc|. Sin (π/3 - θ)
T2 = Ts.|Vc|. Sin (θ)
Sector 1
22

23. Space Vector ModulationSpace Vector Modulation
Reference voltage is sampled at regular interval, T
If T is sampling period,
V1 is applied for T1,
V2 is applied for T2
Zero voltage is applied for the
rest of the sampling period,
T0 = T − T1− T2
T T
Vref is sampled Vref is sampled
V1
T1
V2
T2T0/2
V0
T0/2
V7
va
vb
vc
Within sampling period, vref is synthesized using adjacent vectors and
zero vectors
23

24. Space Vector ModulationSpace Vector Modulation
They are calculated based on volt-second integral of vref






+++=
∫∫∫∫∫ dtvdtvdtvdtv
T
1
dtv
T
1 721o T
0
7
T
0
2
T
0
1
T
0
0
T
0
ref
772211ooref TvTvTvTvTv ⋅+⋅+⋅+⋅=⋅
0TT)60sinj60(cosV
3
2
TV
3
2
0TTv 72
oo
d1doref ⋅+++⋅+⋅=⋅
2
oo
d1dref T)60sinj60(cosV
3
2
TV
3
2
Tv ++⋅=⋅
How do we calculate T1, T2, T0 and T7?
24

25. Space Vector ModulationSpace Vector Modulation
2
oo
d1dref T)60sinj60(cosV
3
2
TV
3
2
Tv ++⋅=⋅
7,021 TTTT ++=
100
V1
Sector 1
α
( )α−α=⋅ sinjcosvv refref
q
d
25

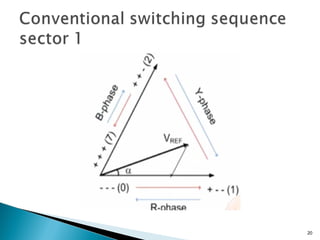
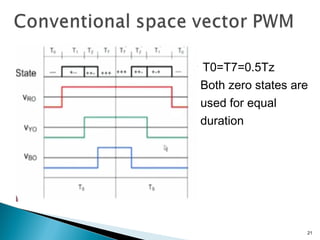
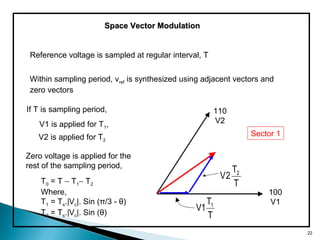
26. Space Vector ModulationSpace Vector Modulation
Solving for T1, T2 and T0,7 gives:
2
oo
d1dref T)60sinj60(cosV
3
2
TV
3
2
Tv ++⋅=⋅
2d1dref TV
3
1
TV
3
2
cosvT +=α 2dref TV
3
1
sinvT =α
T1= 3/2 m[ (T/√3) cos α - (1/3)T sin α ]
T2= mT sin α
where,
M= Vref/ (Vd/ √3)
26

27.  Basic switching vectors and Sectors
Fig. Basic switching vectors and sectors.
 6 active vectors (V1,V2, V3, V4, V5, V6)
 Axes of a hexagonal
 DC link voltage is supplied to the load
 Each sector (1 to 6): 60 degrees
 2 zero vectors (V0, V7)
 At origin
 No voltage is supplied to the load

28. 28

29. 29

30. 30

31. 31

32.  S1 through S6 are the six power transistors that shape
the output voltage. When an upper switch is turned on
(i.e., a, b or c is “1”), the corresponding lower switch is
turned off (i.e., a', b' or c' is “0”).Eight possible
combinations of on and off patterns for the three upper
transistors (S1, S3, S5) are possible.
32

33.  The eight inverter voltage vectors (V0 to V7)
33

34.  The eight combinations, phase voltages and output
line to line voltages
34

35. 35

36. 36

37. 37

38. 38

39. 39

40. 40

41. 41

42. 42

43.  Comparison of Sine PWM and Space Vector PWM
Fig. Locus comparison of maximum linear control voltage
in Sine PWM and SV PWM.
43

44. o
a
b
c
Vdc/2
-Vdc/2
vao
For m = 1, amplitude of
fundamental for vao is Vdc/2
∴amplitude of line-line = dcV
2
3
 Comparison of Sine PWM and Space Vector PWM
44

45.  Comparison of Sine PWM and Space Vector PWM
 Space Vector PWM generates less harmonic distortion
in the output voltage or currents in comparison with sine PWM
 Space Vector PWM provides more efficient use of supply voltage
in comparison with sine PWM
 Sine PWM
: Locus of the reference vector is the inside of a circle with radius of 1/2 Vdc
 Space Vector PWM
: Locus of the reference vector is the inside of a circle with radius of 1/√3 Vdc
∴ Voltage Utilization: Space Vector PWM = 2/√3 or (1.1547) times
of Sine PWM, i.e. 15.47% more utilization of voltage.
45

46. Space Vector ModulationSpace Vector Modulation
Comparison between SVM and SPWM
SVM
We know max possible phase voltage without overmodulation is
∴amplitude of line-line = Vdc
dcV
3
1
Line-line voltage increased by: 100x
V
2
3
V
2
3
V
dc
dcdc −
≈ 15.47%
46

47.  From the simulation results and FFT analysis it is
shown that SVPWM generates less harmonics and
high output voltage for the modulation index given
same for both SPWM and SVPWM techniques.
 Compared to SPWM the Total harmonic distortion
(THD) and lower order harmonics (LOH) contents are
decreased in SVPWM. It is known that the maximum
value of the peak-phase voltage that can be obtained
from a 3-Ph inverter with Sinusoidal Pulse Width
Modulation (SPWM) technique is equal to Vdc/2. It is
therefore evident that SVPWM achieves a better DC
bus utilization compared to SPWM (by about 15.4%).
47

48.  SVM offers better harmonic spectrum. Thus this
scheme is better than sine-triangle PWM scheme.
 Space vector pulse width modulation is new and
the best technique which is ruling the world now.
 Still a lot of research is going on this svpwm.
 It should be available with low cost for household
purpose.
48

49. 1[1]. Hind Djeghloud and Hocine Benalla, “Space Vector Pulse Width Modulation
Applied to The Three-Level Voltage Inverter”, 5th International Conference on
Technology and Automation ICTA’05, Thessaloniki, Greece, Oct 2010.
[2]. Jin-woo Jung, “Space Vector PWM Inverter”, The Ohio State University, February,
2008.
[3]. Jae Hyeong Seo; Chang Ho Choi; Dong Seok Hyun, “A New Simplified space-
Vector PWM Method for Three-Level Inverters”, IEEE Transactions on Power
Electronics, Volume 16, Issue 4, Jul 2010, Pages 545 - 550
[4]. Muhammad H.Rashid “Power Electronics Circuits, devices, and Applications”,
Prentice-Hall of India Private Limited, Third Edition, 2004.
[5]. “the adaptive space vector pwm for four switch three phase inverter fed induction
motor with dc – link voltage imbalance” by Hong Hee Lee*, Phan Quoc Dzung**, Le
Dinh Khoa**, Le Minh Phuong**, Huynh Tan Thanh***School of Electrical Engineering,
University of Ulsan Ulsan, Korea.
[6]. P.S.Bimbhra, “Power Electronics”, Khanna publications.
[7]. Overview of MATLAB Simulink
Http://www.mathworks.com/products/simulink/description/overview.shtml
49

50. 50