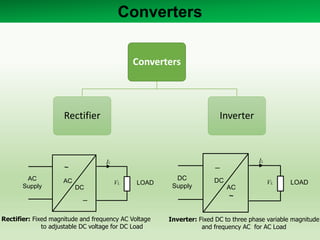
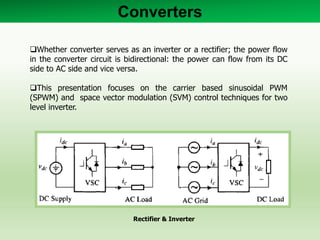
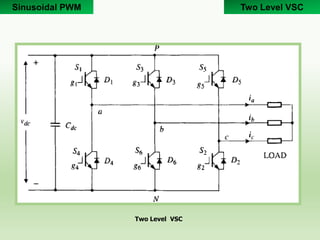
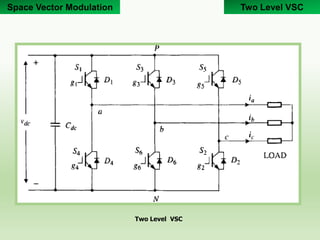
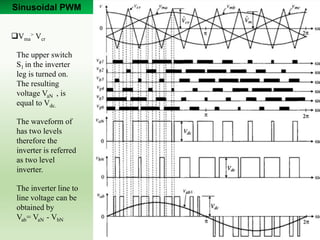
1) The document describes a two level voltage source converter (VSC) that can operate as either a rectifier or inverter using carrier-based sinusoidal pulse width modulation (PWM) or space vector modulation (SVM) control techniques. 2) The two level VSC consists of six switches that can be IGBTs or MOSFETs with anti-parallel diodes, allowing bidirectional power flow between the DC and AC sides. 3) Sinusoidal PWM compares a triangular carrier signal to three-phase modulating waves to generate switching pulses for the converter switches, while SVM represents the converter states as space vectors to calculate switching times.

1. TWO LEVEL VOLTAGE SOURCE CONVERTER
Presented By
FA13-R09-005 Muqadsa Iftikhar
FA13-R09-013 Zunaib Ali
FA13-R09-024 Madiha Naeem

2. Converters
Converters
Rectifier Inverter
LOAD
AC
Supply
VL
IL
~
AC
DC
_
LOAD
DC
Supply
VL
IL
~
DC
AC
_
Inverter: Fixed DC to three phase variable magnitude
and frequency AC for AC Load
Rectifier: Fixed magnitude and frequency AC Voltage
to adjustable DC voltage for DC Load

3. Converters
Whether converter serves as an inverter or a rectifier; the power flow
in the converter circuit is bidirectional: the power can flow from its DC
side to AC side and vice versa.
This presentation focuses on the carrier based sinusoidal PWM
(SPWM) and space vector modulation (SVM) control techniques for two
level inverter.
Rectifier & Inverter

4. Two Level VSC
Circuit diagram for two level voltage source converter is shown.
Converter is composed of six switches S1, S2,…, S6 with an anti-
parallel free wheeling diode for each switch.
Switches can be IGBT, MOSFET depending on power ratings of
converter
Two Level VSC

5. Sinusoidal PWM
Vma, Vmb and Vmc are the three-phase sinusoidal modulating waveforms.
 Vcr is triangular carrier signal.
 The fundamental-frequency component in the inverter output voltage can
be controlled by amplitude modulation index.
The frequency modulation index is

6. Two Level VSC
Two Level VSC
Sinusoidal PWM

7. Sinusoidal PWM
Vma
> Vcr
The upper switch
S1 in the inverter
leg is turned on.
The resulting
voltage VaN , is
equal to Vdc.
The waveform of
has two levels
therefore the
inverter is referred
as two level
inverter.
The inverter line to
line voltage can be
obtained by
Vab= VaN - VbN

8. Sinusoidal PWM
Dead Time
To avoid possible short circuiting of upper and lower devices in an inverter leg a dead
time or blanking time should be implemented during which both the switches must be
turned off.
The switching frequency of the active switches in the two level inverter can be
found from fsw = fcr = fm * mf
The magnitude and frequency of fundamental component Vab1 can be independently
controlled by ma and fm

9. Sinusoidal PWM
Synchronous PWM
 Carrier frequency is varied in accordance with the modulating wave frequency (mf is
an integer)
 Can obtain desired number of pulses and also the optimum pulse width by varying
carrier frequency with modulating frequency, hence harmonics can easily be removed
Need digital circuits for implementation.
Asynchronous PWM
 Carrier frequency is fixed and independent of modulating wave frequency.
No control on number of pulses and also the pulse width as carrier frequency is fixed
hence harmonics are more.
Easily implemented using analogue circuits.

10. Space Vector Modulation
Space vector modulation is one of real time modulation techniques
Widely used in digital control of Voltage source converter
Switching States
The switching state P denotes that the upper switch in an inverter leg is
ON and the inverter terminal voltage is (VaN ,VbN ,VcN) is positive V. as
shown in Table 4-1
Where O denotes that the inverter terminal is zero due to conduction of
the lower switch.

11. Two Level VSC
Two Level VSC
Space Vector Modulation

12. Space Vector Relation with switching states
Table 4-2: Space Vectors, switching states, and on-states switches
The possible eight switching states are shown below in Table 4-2

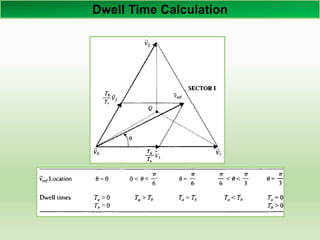
13. Space Vector
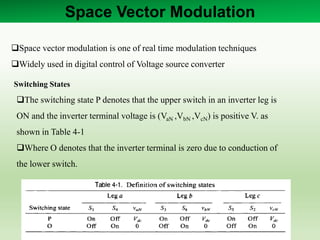
Space Vectors
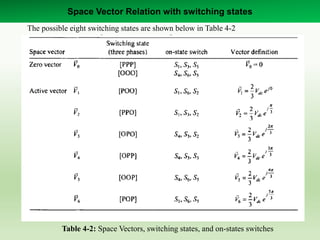
Among the eight switching
states, [PPP] and [OOO] are
zero states and the others are
called active states.
The active and zero
switching states can be
represented by active and zero
vectors, respectively.
Space vector diagram for
two-level inverter is shown
Six vectors V1 to V6 form
hexagon with six equal sectors
and zero vector V0 lies in
center of hexagon

14. Space Vector
Space Vectors
In order to derive relationship between the space vectors and
switching states assume system is balance
Transform 3-phase variables to 2-phase variables through abc/αβ
transformation
A space vector can be generally expressed in terms of 2-phase
voltages in α-β frame

15. Space Vector
For active switching state POO
Following the same procedure all the remaining 6 vectors can be
derived
Vref Will rotates in the space with the angular velocity
R
R R
N
Vdc
3
2
Vdc
3
1
Vdc
3
1

16. Space Vector
The inverter output frequency corresponds to the rotating speed of
Vref where as its output voltage can be adjusted by the magnitude of
Vref
The angular displacement between Vref and the α-axis of the α-β
frame can be obtained by

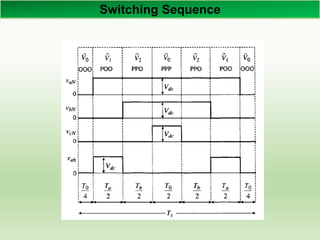
17. Space Vector
+
VDC
-
Vb
Va
Vc
S1 S3 S5
S4 S6 S2
N
R
R R
N
Vdc
3
2
Vdc
3
1
Vdc
3
1
For [POO] the Equivalent Circuit

18. Dwell Time Calculation
The dwell time for the stationary vectors essentially represents
the duty-cycle time of the chosen switches during a sampling
period Ts.
Volt-second balancing principle: product of Vref and sampling
time Ts equals the sum of the voltage multiplied by the time
interval of chosen space vectors

19. Dwell Time Calculation

20. Dwell Time Calculation

21. Modulation Index
As length of reference vector Vref represents the peak value of
fundamental frequency component in inverter output phase
voltage
Va1 is the rms value of the fundamental component

22. Modulation Index
Maximum length of Vref corresponds to radius of the largest
circle i.e. inscribed in the hexagon. Hexagon is formed by 6
active vectors of length 2Vdc/3
Maximum modulation index is

23. Switching Sequence
The switching sequence for given Vref is not unique, but it
should satisfy the following two requirements for minimizing
the device switching frequency.
 the transition from one switching state to the next involves
only two switches in the same inverter leg, one being switched
on and other switched off
 the transition from Vref moving from one sector in the space
vector diagram to the next requires no or a minimum number of
switching.

24. Switching Sequence

25. Switching Sequence
It can be observed that