This document summarizes an effort to update the Curve Number (CN) rainfall-runoff estimation method. A collaborative task group reviewed the state of the CN method and suggested changes based on 60+ years of experience. Key suggestions include relating initial abstraction to soil more accurately, converting CN tables to reflect this change, and calculating runoff from distributed CNs rather than averaged CNs. The proposed changes aim to better represent watershed response processes observed in natural data. Feedback is being solicited on revising relevant chapters in NRCS guidance documents.

1. Updating the Curve Number Method
for Rainfall Runoff Estimation
Tim J. Ward, Ph.D., P.E., F. ASCE, F. EWRI, M. NSPE
Dean and Professor, School of Engineering, Manhattan College, Riverdale, NY
Richard H. Hawkins, Ph.D., P.E., F. ASCE, F. EWRI
Professor Emeritus, University of Arizona, Tucson AZ
Donald E. Woodward, M.S., P.E., F. ASCE
National Hydraulic Engineer, USDA, NRCS (retired), Gaithersburg, MD
73rd Annual SWCS International Conference
July 29 – August 1, 2018
Albuquerque, NM

2. Scope of Presentation
• Results of collaborative review of state-of-practice in Curve
Number (CN) rainfall-runoff estimation method
• Cooperative undertaking by ASCE, ASABE, EWRI and
USDA NRCS – Joint funders of the work
• Collaborative effort by numerous engineers/scientists
• Suggested changes to the CN method
• Revisions of NEH 630 Chapters 8, 9 10, and 12 (2015-2017)

3. Task Group Members and Contributors
Hunter Birckhead, James V. Bonta, Donald Frevert, Claudia
Hoeft* (USDA NRCS liaison), Richard H. Hawkins (Task
Group chair), Rosanna La Plante, Michael E. Meadows,
Julianne Miller, Steven C. McCutcheon, Glenn Moglen, David
Powers, John Ramirez-Avila, E. William Tollner (American
Society of Agricultural and Biological Engineers
representative), Joseph A. Van Mullem, Tim J. Ward (Task
Group co-chair), and Donald E. Woodward (Task Group co-
chair). External reviewers were Bill Elliot, Karen Kabbes, and
Will Thomas. * Special thanks

4. Cooperative Agreement
Signed August 2015 to update NRCS’ NEH Part 630:
• Chapter 8: Land Use and Treatment Classes
• Chapter 9: Hydrologic Soil-Cover Complexes
• Chapter 10: Estimation of Direct Runoff from Storm
Rainfall
• Chapter 12: Hydrologic Effects of Land Use and
Treatment

5. CN Method
• NRCS’ approach to solving hydrology (runoff
from rainfall) for ungauged watersheds. (1954)
• Intended to be a simple procedure to estimate
total storm runoff from total storm rainfall as an
integrated loss function concept. (Intended for and
derived from small upland agricultural watersheds.)
• Used to describe typical watershed response from
infrequent rainfall anywhere in the country, for
watersheds with the same land use, soil
hydrologic group, and surface runoff conditions
• Now used internationally in applications beyond
the original intent.

6. What the CN Method …
Does –
• Estimates runoff depth (volume) from rainfall depth
Does Not –
• Estimates peak discharge
• Estimates hydrograph shape
Those were created separately

7. What is involved
Runoff = f(Rainfall, Watershed Factors)
• Soils
• Cover Conditions
• Land Use
• Antecedent Runoff Condition

8. CN Method - Equations
1. Equation: Q = (P - 0.2S)2 / (P + 0.8S).
with Initial Abstraction coefficient as Ia = 0.2S
2. Tables and charts of CN for soils and land use
CN=1000/(10+S(in))
3. Soils concepts and classifications
4. “AMC” (now ARC) categories

10. Why Update?
• 60+ years of experience showing the shortcomings
• Missing supporting files on reasoning/justification
• Supporting data never published and are hard to find
• The CN Method never underwent a critical peer review
• What is known is from written summaries, institutional
memory, and traditional and entrenched usage

11. A contribution
Curve Number Hydrology: State of the Practice
(ASCE, 2009)

12. How do Curve Numbers really act?
• Variations in rainfall-runoff processes should lead to variations
in CN behavior. [An unexpected fact]
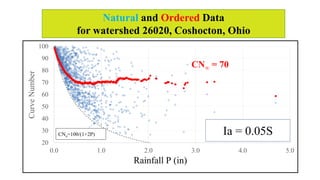
• CN varies with P - An enlightening display [Natural and
Ordered (P, Q) Data Pairs] [There is a lower limit defined as
CNo, i.e., the CN of no runoff for a given P.]
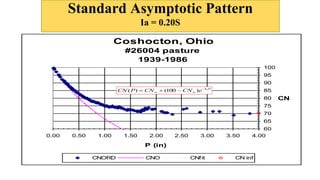
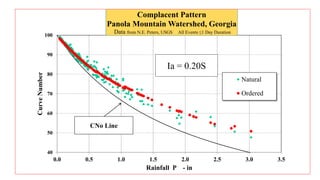
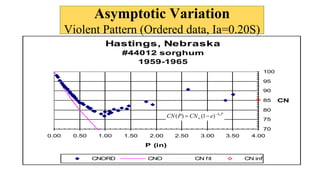
• Three (3) major rainfall-runoff behavior patterns observed
- Standard - Asymptotic
- Violent
- Complacent
(Almost) All watershed P:Q can be so described

13. 20
30
40
50
60
70
80
90
100
0.0 1.0 2.0 3.0 4.0 5.0
CurveNumber
CNo=100/(1+2P)
Rainfall P (in)
Ia = 0.05S
Natural and Ordered Data
for watershed 26020, Coshocton, Ohio
CN∞ = 70

14. Standard Asymptotic Pattern
Ia = 0.20S
Coshocton, Ohio
#26004 pasture
1939-1986
60
65
70
75
80
85
90
95
100
0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50 4.00
P (in)
CN
CNORD CNO CNfit CN inf
Pk
eCNCNPCN 1
)100()( 
 

15. 40
50
60
70
80
90
100
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
CurveNumber
Rainfall P - in
Complacent Pattern
Panola Mountain Watershed, Georgia
Data from N.E. Peters, USGS All Events ≤1 Day Duration
Natural
Ordered
CNo Line
Ia = 0.20S

16. Hastings, Nebraska
#44012 sorghum
1959-1965
70
75
80
85
90
95
100
0.00 0.50 1.00 1.50 2.00 2.50 3.00 3.50 4.00
P (in)
CN
CNORD CNO CN fit CN inf
Asymptotic Variation
Violent Pattern (Ordered data, Ia=0.20S)
Pk
eCNPCN 2
)1()( 
 

17. Primary Suggestions
• Not all watersheds exhibit runoff response to rainfall
that is consistent with the CN method and the method is
not applicable to many forests or karst (leaky)
watersheds downslope of sink holes
• Techniques to determine CN from rainfall runoff data
• Initial abstraction, Ia, is better related to S as Ia = 0.05S

18. Primary Suggestions Continued
• Conversion of current CN0.20 values to CN0.05 values
via Ia conversions
• Total runoff for weighted-average Q from
contributing areas and not weighted-average CN
• NEH 630 CNs based on soils and land use are taken
as CN∞ (steady state or constant CN) at ARCII
(Antecedent Runoff Condition II)

19. 1. Ia  0.05S seems to be better based on numerous studies
2. Q = (P-0.05S0.05)2/(P+0.95S0.05) [revised formulation]
3. “CN” changes too
S∞,0.05 = 1.42S∞,0.20 (Approx., based on natural data, LS fittings)
4. New CN0.05 tables from old CN0.20 (via S)
5. Differences at extremes of low and high rainfalls
Biggest effects with low CN and low P (Low P/S)
Changes to Initial Abstraction (Ia) Relationship with S

20. Averaged Q from distributed CNs
and not from Averaged CN
Qt = Σ(Qi x Ai)/At (with Qi =f(CNi, P) [1]
and not
Qt = f(CNc [= Σ(CNi x Ai)/At], P) [2]
[when [1] is used, results will normally display as a standard CN:P
pattern]

21. Effects of Suggested Changes
• Averaged Q and not Averaged CN – Little effecton major
floods but a better representation of runoff generation
process, and more realistically show “smaller” storm
responses and asymptotic pattern.
• Change in Ia (and CN) – Higher Q at low P and low CN;
More comparable with current approach at higher P.
• Suggested changes do not include changes to hydrograph
generation - the NRCS lag equation, unit hydrograph
parameters, or peak discharge-storage relationship.

22. Outstanding Issues
• Non - CN watersheds, such as some forests and karst,
others
• New land uses/types – urbanization, LIDs, solar
farms, green roofs
• Fire effects
• Small storms and water quality planning
• Hydrograph methods and other directives

23. What Next?
• The NRCS has distributed the revised chapters to the
individual state levels and encourage critique and
comments.
• The ASCE has posted the chapters in its Collaborate system
to solicit feedback.
• The Task Group is still functional and will respond to the
comments and feedback.

24. Questions and Comments?