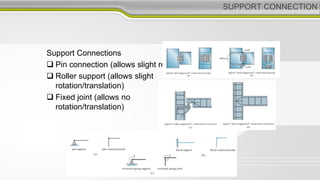
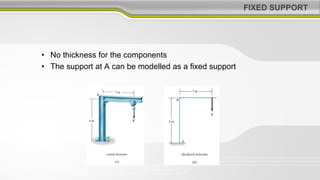
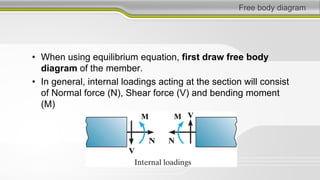
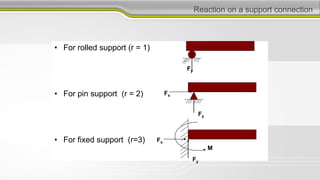
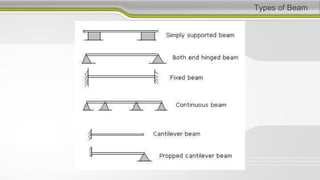
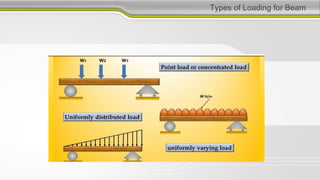
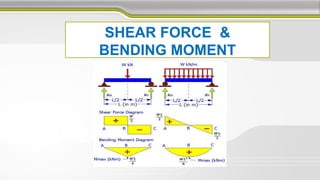
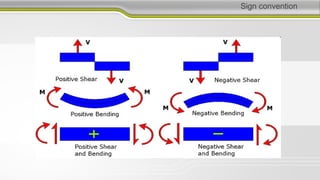
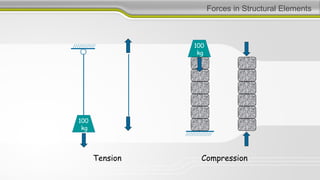
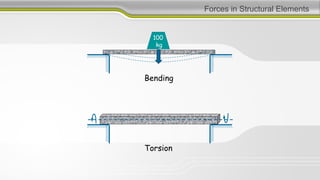
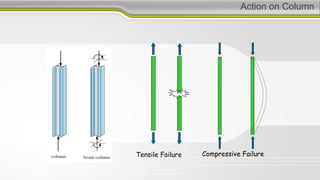
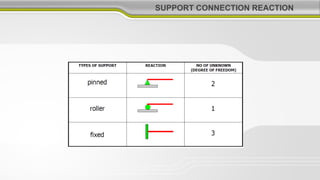
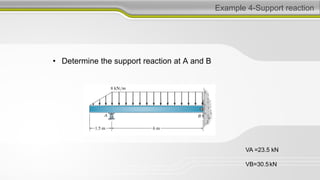
This document discusses structural analysis and beam analysis. It covers topics such as support reactions, shear force and bending moment diagrams, equilibrium of forces in structures, and determinacy. Key points include: 1. To design structures, it is necessary to know bending moments, torsion moments, shear forces, and axial forces in each member. 2. Equilibrium requires that the downward forces from gravity have equal and opposite upward reaction forces. 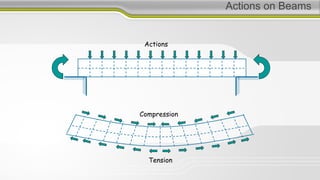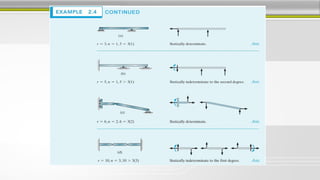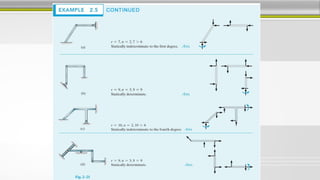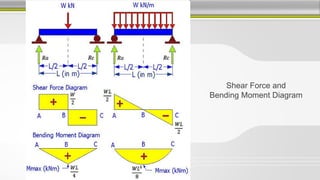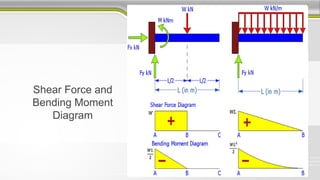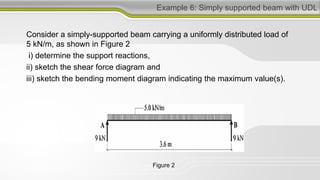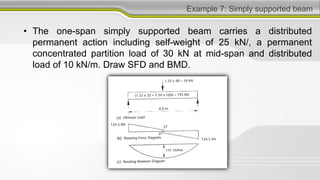3. Shear force and bending moment diagrams show the variation of these internal forces along a beam under different loading conditions.

1. SITI KAMARIAH MD SA’AT
FKTM
UNIMAP
STRUCTURAL ANALYSIS
BEAM ANALYSIS
MMJ34103
FARM STRUCTURAL DESIGN

2. STRUCTURAL ANALYSIS
Support Reaction
Shear Force and Bending Moment

3. Information
• To design a structure it is necessary to know in each member:
1. Bending moments
2. Torsion moments
3. Shear forces
4. Axial forces

4. Equilibrium
• The goal of the whole design process is to achieve an equilibrium of the
forces acting upon a structure.
• Without equilibrium the building will move and that is not good
• For all of the forces acting downward due to gravity, an equal, opposite force
called a reaction must be pushing up.
• All of the loads acting on a structure will ultimately accumulate in the
foundation and must be met with an equivalent reaction from the earth
below.

5. Forces
• Forces are a type of quantity called vectors
– Defined by magnitude and direction
• Statement of equilibrium
– Net force at a point in a structure = zero (summation of forces = zero)
• Net force at a point is determined using a force polygon to
account for magnitude and direction

6. Forces in Structural Elements
100
kg
Compression
100
kg
Tension

7. Forces in Structural Elements
100
kg
Bending
Torsion

8. Actions on Beams
Tension
Compression
Actions

9. Action on Column
Tensile Failure Compressive Failure

10. SUPPORT CONNECTION
Support Connections
 Pin connection (allows slight rotation)
 Roller support (allows slight
rotation/translation)
 Fixed joint (allows no
rotation/translation)

11. SUPPORT CONNECTION
• In reality, all connections and supports are modelled with assumptions.
• Need to be aware how the assumptions will affect the actual
performance.

12. FIXED SUPPORT
• No thickness for the components
• The support at A can be modelled as a fixed support

13. Pin connection
Roller connection
Fixed connection

14. Static equilibrium
• The state of an object when it is at rest or moving with a
constant velocity.
• There may be several forces acting on the object.
• If they are canceling each other out and the object is not
accelerating, then it is in a state of static equilibrium.

15. Static Equilibrium
• Since the externally applied force system is in equilibrium, the
three equations of static equilibrium must be satisfied, i.e.
• +ve ↑ ΣFy = 0 The sum of the vertical forces must equal zero.
• +ve ΣM = 0 The sum of the moments of all forces about any
point on the plane of the forces must equal zero.
• +ve → ΣFx = 0 The sum of the horizontal forces must equal zero.
* The assumed positive direction is as indicated.

16. Equations of Equilibrium
• A structure or one of its
members in equilibrium is called
statics member when its balance
of force and moment.
• In general this requires that force
and moment in three
independent axes, namely
0
,
0
0
,
0
0
,
0
=
=
=
=
=
=
∑
∑
∑
∑
∑
∑
z
z
y
y
x
x
M
F
M
F
M
F

17. Equations of Equilibrium
• In a single plane, we consider
0
0
0
=
=
=
∑
∑
∑
M
F
F
y
x

18. Free body diagram
• When using equilibrium equation, first draw free body
diagram of the member.
• In general, internal loadings acting at the section will consist
of Normal force (N), Shear force (V) and bending moment
(M)

19. Determinacy and Stability
• Statically Determinate r = 3n
• Statically Indeterminate r > 3n
• Unstable r < 3n
Where r = reaction
n = parts

20. Determinacy and Stability
• If the reaction forces can be determined solely from the
equilibrium EQs → STATICALLY DETERMINATE STRUCTURE
• No. of unknown forces > equilibrium EQs → STATICALLY
INDETERMINATE STRUCTURE
• Can be viewed globally or locally (via free body diagram)

21. Determinacy of beam
• Determinacy and Indeterminacy
– For a 2D structure
ate
indetermin
statically
,
3
e
determinat
statically
,
3
n
r
n
r
>
=
No. of force and moment
reaction components
No. of parts
mechanism
e
collapsibl
a
form
component
or
parallel
or
consurrent
are
reaction
member
if
unstable
:
3n
r
unstable
@
acy
indetermin
of
degree
:
3
≥
< n
r

22. Reaction on a support connection
• For rolled support (r = 1)
• For pin support (r = 2)
• For fixed support (r=3)
Fy
Fy
Fx
Fy
Fx
M

23. SUPPORT CONNECTION REACTION

24. EXAMPLES
DETERMINACY
STATIC EQUILIBRIUM

25. Example 1
• Classify each of the beams as statically determinate or statically
indeterminate. If statically indeterminate, report the no. of degree
of indeterminacy. The beams are subjected to external loadings
that are assumed to be known & can act anywhere on the beams.

27. Example 2
• Classify each of the pin-connected structures as statically
determinate or statically indeterminate. If statically
indeterminate, report the no. of degree of indeterminacy.
The structures are subjected to arbitrary external loadings
that are assumed to be known & can act anywhere on the
structures.

29. APPLICATION OF EQUATION
OF EQUILIBRIUM

30. Procedure of Analysis
• Disassemble the structure and draw a free–body
diagram of each member.
Free Body Diagram
• The total number of unknowns should be equal to
the number of equilibrium equations
Equation of Equilibrium

31. Example 4-Support reaction
• Determine the support reaction at A and B
VA =23.5 kN
VB=30.5kN

32. Types of Beam

33. Types of Loading for Beam

34. SHEAR FORCE &
BENDING MOMENT

35. Shear Force & Bending Moment
• Two parameters which are fundamentally important to the
design of beams are shear force and bending moment.
• These quantities are the result of internal forces acting on
the material of a beam in response to an externally applied
load system.

36. Sign convention

37. Shear Force Diagram (SFD)
• The calculation carried out to determine the shear force can be
repeated at various locations along a beam and the values obtained
plotted as a graph; this graph is known as the shear force diagram.
• The shear force diagram indicates the variation of the shear force
along a structural member.

38. Bending Moment Diagram
• Bending inducing tension on the underside of a beam is
considered positive.
• Bending inducing tension on the top of a beam is
considered negative.

39. Bending Moment Diagram
• Note: Clockwise/anti-clockwise moments do not define +ve or
−ve bending moments.
• The sign of the bending moment is governed by the location of the
tension surface at the point being considered.
• As with shear forces the calculation for bending moments can be
carried out at various locations along a beam and the values
plotted on a graph; this graph is known as the‘bending moment
diagram’.
• The bending moment diagram indicates the variation in the
bending moment along a structural member.

40. Shear Force and Bending Moment Diagram
• If the variations of V & M are plotted, the graphs are termed the shear
diagram and moment diagram
• Changes in shear= Area under distributed load diagram
• Changes in moment = Area under shear diagram

41. Shear Force and
Bending Moment Diagram

42. Shear Force and
Bending Moment
Diagram

43. Examples

44. Example 5 : Simply supported beam with point loads
Consider a simply supported beam as shown in Figure 1 carrying a
series of secondary beams each imposing a point load of 4 kN.
• i) determine the support reactions,
• ii) sketch the shear force diagram and
• iii) sketch the bending moment diagram indicating the maximum
value(s).
Figure 1: Simply supported beam

45. solution

46. Example 6: Simply supported beam with UDL
Consider a simply-supported beam carrying a uniformly distributed load of
5 kN/m, as shown in Figure 2
i) determine the support reactions,
ii) sketch the shear force diagram and
iii) sketch the bending moment diagram indicating the maximum value(s).
Figure 2

47. Example 7: Simply supported beam
• The one-span simply supported beam carries a distributed
permanent action including self-weight of 25 kN/, a permanent
concentrated partition load of 30 kN at mid-span and distributed
load of 10 kN/m. Draw SFD and BMD.

48. PRACTICE MAKES PERFECT!!!