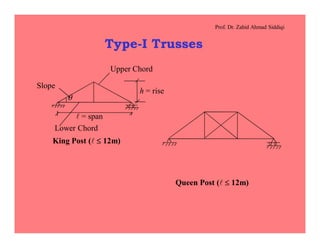
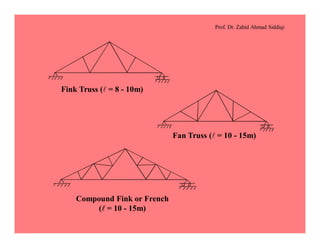
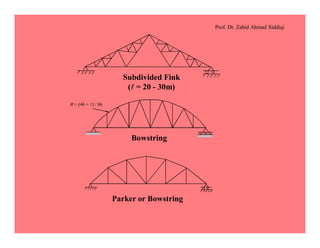
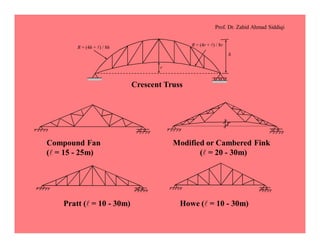
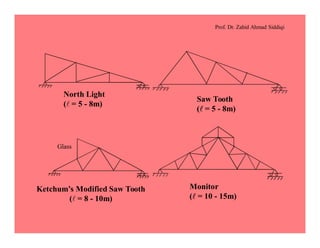
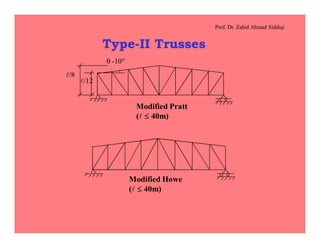
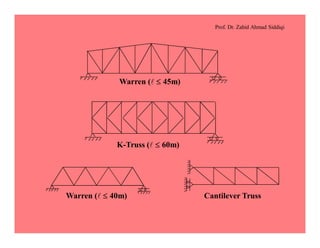
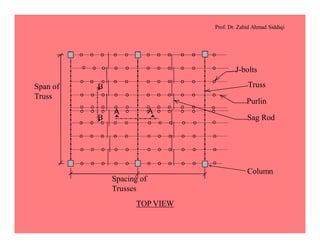
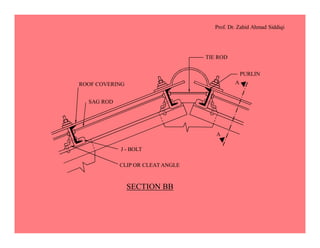
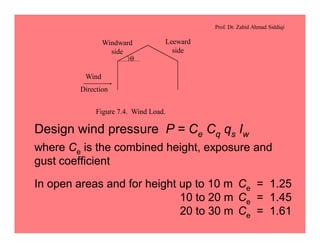
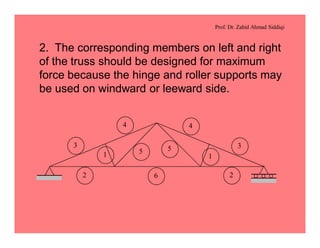
This document discusses the properties and analysis of trusses. It defines a truss as a frame structure where all members experience axial forces. Trusses are analyzed as pin-jointed frames if the joints intersect at a single point and loads are only applied at panel points. The document compares trusses to rigid frames and outlines various truss types including common roof trusses like the Howe, Pratt, Fink and Warren trusses. It also defines related terms like pitch, rise, purlins and loads on truss roofs.

1. Prof. Dr. Zahid Ahmad Siddiqi
PROPERTIES OF TRUSSES
Truss is a frame structure in which all the
members have axial forces due to the
following facts:
a. Members are arranged in triangles for
stability.
b. All the joints of a truss are actually
semi-rigid or fully rigid. However,
theoretically, these joints may be
considered as pin joints.

2. Prof. Dr. Zahid Ahmad Siddiqi
The analysis as a pin-jointed frame is
valid provided that the requirements
given in No.3 and 4 are satisfied.
c. Centroidal axes of all the members
meeting at a joint must intersect at a
single point.
d. The loads are only applied at the panel
points.

3. Prof. Dr. Zahid Ahmad Siddiqi
Following is the comparison between rigid
frames and trusses:
a. Joints are considered as having frictionless pins in
trusses with no moment at the member ends. In case
of rigid frames, the members are rigidly connected
having appreciable moments at the member ends.
b. The forces in case of trusses are only axial and
hence the members are equally stressed throughout
their cross-section. In rigid frames, due to bending
moment, the fibers of the cross-section away from
the neutral axis have maximum stresses and the
fibers close to the neutral axis have less stress.

4. Prof. Dr. Zahid Ahmad Siddiqi
c. Because of the above facts, the design of a member
in a case of a truss is economical as compared with
the members of a rigid frame. Hence, trusses become
economical in those cases where the corresponding
construction cost is less as a percentage of the total
cost.
TYPES OF TRUSSES
Trusses can broadly be divided into two
categories, Type -I trusses are preferred in
those areas where snowfall is common and
Type-II trusses used in cot climates.

5. Prof. Dr. Zahid Ahmad Siddiqi
The roofs of Type-I trusses are inclined at
greater angles (10° to 60°) to drain part of the
snow falling on the roof surface.
These may also be preferred if bending
moments are larger near the mid-span and
zero at the ends.
The roofs of Type-II trusses are either nearly
flat or are inclined at angles less than 10°.

6. Prof. Dr. Zahid Ahmad Siddiqi
Type-I Trusses
q
Slope
h = rise
Upper Chord
l = span
Lower Chord
King Post (l £ 12m)
Queen Post (l £ 12m)

7. Prof. Dr. Zahid Ahmad Siddiqi
Fink Truss (l = 8 - 10m)
Fan Truss (l = 10 - 15m)
Compound Fink or French
(l = 10 - 15m)

8. Prof. Dr. Zahid Ahmad Siddiqi
Subdivided Fink
(l = 20 - 30m)
R = (4h + l) / 8h
Bowstring
Parker or Bowstring

9. Prof. Dr. Zahid Ahmad Siddiqi
R = (4h + l) / 8h R = (4r + l) / 8r
h
r
Crescent Truss
r
Compound Fan Modified or Cambered Fink
(l = 15 - 25m) (l = 20 - 30m)
Pratt (l = 10 - 30m) Howe (l = 10 - 30m)

10. Prof. Dr. Zahid Ahmad Siddiqi
If the forces in the diagonal members are all compressive and
that in the vertical members are all tensile, the truss is called
Howe Truss.
In a reverse way if the forces in all the diagonal members are
tensile while the forces in all the vertical members are
compressive, the truss is called Pratt Truss.
The difference between these two trusses is only the
orientation of the diagonals in relation to the applied loads.
In case of Warren Truss, the diagonals alternate in
orientation and also in the sense of forces in them. For all the
roof trusses, the loads are in general applied on the top
chord.

11. Prof. Dr. Zahid Ahmad Siddiqi
Glass
North Light
(l = 5 - 8m)
Saw Tooth
(l = 5 - 8m)
Ketchum’s Modified Saw Tooth
(l = 8 - 10m)
Monitor
(l = 10 - 15m)

12. Prof. Dr. Zahid Ahmad Siddiqi
Type-II Trusses
l/12
l/8
0 -10°
Modified Pratt
(l £ 40m)
Modified Howe
(l £ 40m)

13. Prof. Dr. Zahid Ahmad Siddiqi
Warren (l £ 45m)
K-Truss (l £ 60m)
Warren (l £ 40m) Cantilever Truss

14. Prof. Dr. Zahid Ahmad Siddiqi
TERMS RELATED WITH TRUSSES
Pitch of a Roof Truss
Pitch of a roof truss is defined as the maximum
rise of top chord of the truss (h) divided by total
span of the truss. For symmetrical trusses the
pitch is equal to double the inclination of the top
chord.
pitch = h / l

15. Prof. Dr. Zahid Ahmad Siddiqi
Inclination of a Roof Truss
The slope (tanq) or angle (q) of top chord of a
truss with respect to the horizontal is called
inclination of the truss.
For un-symmetrical trusses, inclination may
be completely independent of the pitch of the
trusses.
For type-I trusses, q £ 60°
with most suitable range of 20° - 30°.
For type-II trusses, q £ 10°

16. Prof. Dr. Zahid Ahmad Siddiqi
Height / Rise of Truss
The maximum height of the truss (h) with respect
to the ends of the bottom chord is called height or
rise of a truss. The highest point is called crown
of the truss.
For type-I trusses, h = l /3 to l /5
with most suitable value of l /4.
For type-II trusses, h = l /8 to l /12
with most suitable value of l /10.

17. Prof. Dr. Zahid Ahmad Siddiqi
Panel Length
In case of roof trusses, the distance between
two consecutive top chord joints is known as
the panel length.
Panel lengths can be the projected horizontal
or the actual inclined lengths.
Panel length for type-I trusses = 1 to 3m
with most appropriate value of 1.8m.
Panel length for type-II trusses = 3 to 4m

18. Prof. Dr. Zahid Ahmad Siddiqi
Purlins
These are small beams that run perpendicular to the
trusses and rest at the panel points of the trusses.
The purlins provide lateral bracing to the top chord
and carry the load of the roof transferring it to the
panel points of the trusses.
The span of these beams is equal to the center-to-
center spacing of the trusses.
Usually the purlins are continuous over the trusses
but are designed as simply supported for
convenience of design and construction.

19. Prof. Dr. Zahid Ahmad Siddiqi
B
B
A A
J-bolts
Truss
Purlin
Sag Rod
Spacing of
Trusses
Span of
Truss
Column
TOP VIEW

20. Prof. Dr. Zahid Ahmad Siddiqi
CLIP OR CLEAT ANGLE
J - BOLT
SAG ROD
ROOF COVERING
TIE ROD
PURLIN
A
A
SECTION BB

21. Prof. Dr. Zahid Ahmad Siddiqi
SECTION AA
C – SECTION PURLIN
CLEATANGLE
TOP CHORD OF TRUSS
Clip or Cleat Angles
These angles are previously bolted, riveted, or
welded to the top chord above which the purlin
may rest while it is being fastened to the truss.

22. Prof. Dr. Zahid Ahmad Siddiqi
Sag Rods
When channels are used for purlins, it is good
design practice to use sag rods to take the
tangential component of the roof loads.
These are placed either at mid span or at the third
points, depending on the weight of the roof, the
span of the purlins, and the pitch of the roof truss.
Max. span of purlin for one sag rod = 6 m (light roofing)
= 4.5 m (heavy roof with pitch £ 1/4)
For roofs steeper than a pitch of 1/4, two sag rods should be
used for a purlin span of 4.5m.

23. Prof. Dr. Zahid Ahmad Siddiqi
Roof Covering/Sheathing
Light roofing: Corrugated Galvanized Iron
(G.I.) sheets
Corrugated Asbestos Cement
Concrete (A.C.C.) sheets.
Heavy roofing: Clay or cement tiles
Gypsum tiles
Slate tiles
Tar plus gravel

24. Prof. Dr. Zahid Ahmad Siddiqi
J-Bolt
J-bolt, also called hook bolt, is a bolt in the
form of letter “J” used to fix roof-sheathing or
wall sheathing to purlins and other structural
members.
Eave
The end of truss lower in level along with its
support is called eave of the truss.

25. Prof. Dr. Zahid Ahmad Siddiqi
Eave’s Gutter
A channel is provided at eave-level to collect
rainwater, which is called eave’s gutter.
Rafter
Sometimes beams in addition to purlins (in a
perpendicular direction) are provided to support
the roof called rafters.
Strut
Relatively short length columns without the
chances of buckling are called struts.

26. Prof. Dr. Zahid Ahmad Siddiqi
Spacing of Roof Trusses
Span of
truss (m)
Center-to-
center spacing
(m)
15-18 3.5-6
27-30 4.5-7.3
> 42 15-18
For very large spacing of trusses, purlins may
themselves be provided in the form of trusses.

27. Prof. Dr. Zahid Ahmad Siddiqi
LOADS ON TRUSS ROOVES
All the gravity or vertical loads acting on the
building trusses are first calculated in terms of
the loads acting per one square meter of the
horizontally projected area (or plan area)
having the units N/m2 or kN/m2.
The wind loads are calculated per square
meter of the actual inclined roof surface in the
same units.

28. Prof. Dr. Zahid Ahmad Siddiqi
Dead Loads
Dead load is the self weight of different
components of the structure itself.
Its magnitude and point of application does
not appreciably change with time.
Dead load on a truss will comprise of loads
of roof coverings, perpendicularly running
beams (called purlins), connections,
supporting elements (called braces) and self
load of the truss.

29. Prof. Dr. Zahid Ahmad Siddiqi
Superimposed Loads
All the loads externally acting on the
structure leaving its own weight are called
superimposed loads.
Dead Loads of Truss Roof Components
The weights of various structural
components per unit plan area are as
follows:

30. Prof. Dr. Zahid Ahmad Siddiqi
a) Asbestos cement concrete sheets (corrugated) 150-300 N/m2
b) Corrugated galvanized iron sheets 60-300 N/m2
c) Light weight R. C. slabs, 60-90 mm thick. 1200-2000 N/m2
d) Slate, Gypsum and other tiles. 350-400 N/m2
e) Glazing 6 mm or wire woven glass. 250-300 N/m2
f) Tar & gravel roofing. 400-500 N/m2
g) Insulation boards. 50-80 N/m2
h) Purlins i) For slate roof. 100-150 N/m2
ii) For glazed roof. 75-125 N/m2
iii) For corrugated sheeting. 60-90 N/m2
i) Bracings 15-60 N/m2
j) Miscellaneous. 50-70 N/m2
k) Self weight of truss. 100-250 N/m2

31. Prof. Dr. Zahid Ahmad Siddiqi
To obtain a better estimate of the truss self
weight for a 4 m spacing of trusses and a
pitch of 1/4 to 1/5 with corrugated sheeting,
weight per unit area of plan may be taken as:
10
3
5 2Spanin metres
N m+
é
ë
ê
ù
û
ú /
whereas, for all other cases, the Thayer
Formula may be used:
W = ( )
w
S
L0 37 170. .+

32. Prof. Dr. Zahid Ahmad Siddiqi
whereW = Weight of truss (N/m2)
w = Total load per horizontal plan
acting on the truss (N/m2)
S = Spacing of truss (m)
L = Span of the truss (m)
Snow Load
Snow load is calculated according to max. expected
depth of snow in a particular locality and density of
snow.
Maximum density of snow = 7860 N/m3
The density of snow significantly varies with the
amount of compactness.

33. Prof. Dr. Zahid Ahmad Siddiqi
Live Load (or Minimum Snow Load)
1000 N/m2 for q £ 10° for no access to roof.
2000 N/m2 for q £ 10° when access is provided to
roof.
(1130 - 13q) N/m2 for 10° < q £ 20°
(1430 - 28q) N/m2 for 20° < q £ 30°
600 N/m2 for q > 30°
Wind Load
The windward side is the face of the building
towards wind and the leeward side is the
face of the building opposite to wind.

34. Prof. Dr. Zahid Ahmad Siddiqi
q
Wind
Direction
Windward
side
Leeward
side
Figure 7.4. Wind Load.
Design wind pressure P = Ce Cq qs Iw
where Ce is the combined height, exposure and
gust coefficient
In open areas and for height up to 10 m Ce = 1.25
10 to 20 m Ce = 1.45
20 to 30 m Ce = 1.61

35. Prof. Dr. Zahid Ahmad Siddiqi
qs = wind stagnation pressure at the
standard height of 10 m.
= 0.0475 V 2 (N/m2)
where
V = basic wind velocity in km/h
Iw = 1.0 for ordinary buildings.
P = 1250 Cq (N/m2) for V=145 km/h and
height up to 10m in open areas.

36. Prof. Dr. Zahid Ahmad Siddiqi
Value of Pressure Coefficient (Cq)
Windward roof
q = 0° to 9.5° Cq = 0.7 outward
9.5° to 37.0° Cq = 0.9 outward or
0.3 inward
which ever is critical
37° to 45° Cq = 0.4 inward
> 45° Cq = 0.7 inward
Leeward or flat roof Cq = 0.7 outward

37. Prof. Dr. Zahid Ahmad Siddiqi
Windward walls
Cq = 0.8 inward up to 6m height
0.87 inward for 6 to 12m height
1.0 inward for 12 to 18m height
Leeward walls
Cq = 0.5 inward up to 6m height
0.54 inward for 6 to 12m height
0.63 inward for 12 to 18m height

38. Prof. Dr. Zahid Ahmad Siddiqi
SELECTION OF MEMBERS OF
ROOF TRUSSES
1. For riveted and bolted trusses a pair of
angles back-to-back is the most common type of
member. For short spans and lightly loaded
trusses, a single angle is sometimes used,
mainly for tension members.
2. For larger riveted or bolted roof trusses T, W,
M, S, or two channels back-to-back sections may
be used for some of the members.

39. Prof. Dr. Zahid Ahmad Siddiqi
3. The two sections of a member are connected at
internals by filler plates (stay plates) with welding or
riveting to give slenderness ratio of single section
(where the two sections are not joined) lesser than
the slenderness ratio of the double section.
4. A minimum size member for practical reasons to
avoid too flimsy sections is often 2Ls 51 ´ 51 ´ 6.4.
5. An effort should be made to limit the width of
truss members because it has been found that
trusses with very wide members tend to have large
secondary forces.

40. Prof. Dr. Zahid Ahmad Siddiqi
6. The chord members of roof trusses often
consist of one section which is continuous
through several panel points. This may be
designed for the maximum force in any of the
parts in which it is continuous.
7. If structural T is used as top chord member for
a welded truss, gusset plates may be
unnecessary for top chord and web members
can be welded directly to the stems of the tees.

41. Prof. Dr. Zahid Ahmad Siddiqi
Selection of Truss Members Using
Angle Sections
1. For top chord members which are adjacent to
each other and have a force up to 25% lesser than
the maximum out of these members, same section
could be used which is designed for the maximum
force member.
However, for all other top chord members, same
depth section should be selected.
Same procedure applies to bottom chord members.

42. Prof. Dr. Zahid Ahmad Siddiqi
2. The corresponding members on left and right
of the truss should be designed for maximum
force because the hinge and roller supports may
be used on windward or leeward side.
3
1
2
4
5
6
4
3
1
2
5

43. Prof. Dr. Zahid Ahmad Siddiqi
3. All top and bottom chord members should be
double angles.
4. All compression members should be double
angles.
5. Web tension members may be single or double
angles depending upon the magnitude of force.
6. Zero force members should be single angles.
7. Stay plate spacing should be calculated for all
double angle sections.