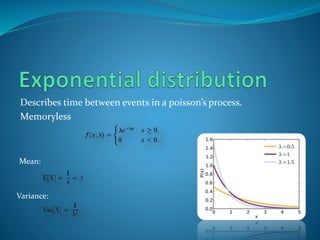
The document describes several common probability distributions used to model random phenomena, including the binomial, geometric, negative binomial, Poisson, uniform, and exponential distributions. It provides the probability mass or density functions that define each distribution, as well as the mean and variance formulas. Examples are given for how each distribution can be applied to problems involving random events like coin flips, dice rolls, polling, customer arrivals, and more.

2. To describe random phenomena
Where Only integer values

3. Repeated experiment:
 Two outcomes:
Repetitions allowed
Independent trials
Probability remains constant
Success or failure
Consider an expt. Of n trials
Let
Xj=1 (if jth expt resultedin a success)
And
Xj=0 (ifjthexptresultedin a failure)
thusprobability:
P(X1,X2,X3…….Xn) = P1(X1).P2(X2)………Pn(Xn)
And
Pj(Xj) = P(Xj) = {
P, Xj=1, j=1,2….n
1-P=Q Xj=0, j=1,2….n
0, otherwise
For 1 trial, this is called the
bernoulli distribution

4. Flipping a coin. In this context, obverse ("heads") conventionally
denotes success and reverse ("tails") denotes failure.
Rolling a die, where a six is "success" and everything else a "failure".
In conducting a political opinion poll, choosing a voter at random to
ascertain whether that voter will vote "yes" in an upcoming
referendum.
Mean and variance:
•Mean:
E(Xj)= 0.q+1.p=P
•Variance:
V(Xj)=[(0.q)+(12.p)]-p2=P(1-P)

5. Repetition of trials
Two outcomes
Independent trials
Probability remains constant
•Random variable X denoting no. of n bernoulli trials has a binomial
distribution given by:
P(X) = {
•Taking outcome with all successes(S) and failures(F)
We get:
( ) = n!/x!(n-x)!
Where P(SSS….SS FF…….FF)=pxqn-x
( ) pX qn-X ,x=0,1,2…..n
0 ,otherwise
n
x
n
x

6. Mean and variance:
X – sum of n independnet bernoulli random variables
•Mean:
E(X)=P+P……+P=nP
•Variance:
V(X)=PQ+PQ+……+PQ=nPQ
•when n = 1, the binomial distribution is a Bernoulli
distribution

7. P(6)=1/6
P(6’)=5/6
P(6)=1/6
P(6’)=5/6
P(6)=1/6
P(6’)=5/6
P(6)=1/6 P(6)=1/6
P(6’)=5/6
P(6)=1/6
P(6’)=5/6
P(6’)=5/6

8. •Assume Bernoulli trials
•Let X denote the number of trials until the first success. Then, the probability
mass function of X is:
P(X=x)=(1−p)x−p
For x = 1, 2, ... In this case, we say that X follows a geometric distribution.
Mean and variance:
•The mean of a geometric random variable X is:
E(X)=1/p
•The variance of a geometric random variable X is:
V(X)=1−p/p2

9. Assume Bernoulli trials
•Let X denote the number of trials until the rth success.
P(X=x)=(x−1r−1)(1−p)x−rpr
for x = r, r + 1, r + 2, ... In this case, we say that X follows a negative
binomial distribution.
Note two things:
(1) There are (theoretically) an infinite number of negative binomial distributions.
(2) A geometric distribution is a special case of a negative binomial distribution with r = 1.
Mean and variance:
The mean of a negative binomial random variable X is:
E(X)=r/p
The variance of a negative binomial random variable X is:
V(x)=r(1−p)/p2

10. If X is a Poisson random variable
P(x)=e−λλx/x!
for x = 0, 1, 2, ... and λ > 0
Examples
•Let X equal the number of typos on a printed page.
•Let X equal the number of cars passing through the intersection of Allen
Street and College Avenue in one minute.
•Let X equal the number of customers at an ATM in 10-minute intervals.
•Let X equal the number of students arriving during office hours.
Mean and variance:
The mean of a Poisson random variable X is λ.
The variance of a Poisson random variable X is λ.

11. To describe random phenomena
Where Any value

12. A continuous random variable X has a uniform distribution,
denoted U(a, b), if its probability density function is:
P(x)=1/b−a
for two constants a and b, such that a < x < b.

13. The mean of a continuous uniform random variable defined over the
support a < x < b is:
E(X)=a+b/2
The variance of a continuous uniform random variable defined over the
support a < x < b is:
V (X)=(b−a)2/12

14. Describes time between events in a poisson’s process.
Memoryless
Mean:
Variance:

15. To sample exponentional,uniform,triangular dist.
Form empirical dist.
Straight forward