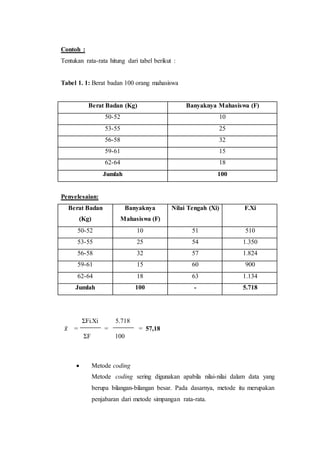
Teks tersebut membahas tentang ukuran-ukuran pemusatan data seperti rata-rata, median, dan modus. Rata-rata digunakan untuk mewakili seluruh data, median untuk menemukan nilai tengah, dan modus untuk menemukan nilai yang paling sering muncul. Contoh soal juga diberikan untuk menjelaskan cara menghitung ketiga ukuran tersebut.

1. TUGAS STATISTIK EKONOMI & BISNIS I
Oleh:
WINDA ANGGRENI
1615310004
PROGRAM STUDI MANAJEMEN
UNIVERSITAS PANCA BUDI
MEDAN
2017

2. BAB III
Ukuran Pemusatan Data
Ukuran Pemusatan Data merupkan ukuran yang dapat melihat bagaimana data
tersebut mengumpul. Ukuran pemusatan data yaitu mencari sebuah nilai yang
dapat mewakili dari suatu rangkaian data.
Macam-macam ukuran pemusatan data:
a) Rata-rata hitung (mean)
b) Median
c) Modus
1. Rata-rata hitung (mean)
Rata-rata hitung (mean) adalah nilai rata-rata dari data-data yang tersedia.
Rata-rata hitung dari populasi diberi simbol: µ (baca: miu). Rata-rata
hitung dari sampel diberi simbol: 𝑥̅ (baca: eks bar). Menentukan rata-rata
hitung secara umum dapat dirumuskan:
Rata-rata hitung = Jumlah Semua Nilai Data
Jumlah Data
1) Rata-rata hitung (mean) untuk data tunggal
 Jika X1, X2, ... Xn merupakan n buah nilai dari variabel X, maka
rata-rata hitungnya sebagai berikut :
ΣX X1 + X2 +...+ Xn
𝑥̅ = =
n n
i = 1,2,3...
Keterangan:
𝑥̅ = rata-rata hitung (mean)
Xi = Waki data
n = jumlah data

3.  Jika Xi, X2, ... Xn masing-masing memiliki frekuensi f1, f2,...,fn, maka
rata-rata hitungnya sebagai berikut :
ΣFi F1X1 + F2x2 + ... + FnXn
𝑥̅ = =
ΣF F1 + F2 + ... Fn
Contoh :
Nilai ulangan matematika Anto pada semester 1 adalah 6, 8, 5, 7, 9, dan 7. Maka
rata-ratanya adalah :
6 + 8 + 5 + 7 + 9 + 7 42
𝑥̅ = = = 7
6 6
2) Rata- rata hitung (mean) untuk data kelompok
 Metode biasa
Apabila telah dibentuk distribusi frekuensi biasa, dengan Fi =
frekuensi pada interval kelas ke-i, maka rata-rata hitung (mean) dapat
dihitung dengan rumus :
ΣFi. Xi
𝒙̅ =
ΣF

4. Contoh :
Tentukan rata-rata hitung dari tabel berikut :
Tabel 1. 1: Berat badan 100 orang mahasiswa
Berat Badan (Kg) Banyaknya Mahasiswa (F)
50-52 10
53-55 25
56-58 32
59-61 15
62-64 18
Jumlah 100
Penyelesaian:
Berat Badan
(Kg)
Banyaknya
Mahasiswa (F)
Nilai Tengah (Xi) F.Xi
50-52 10 51 510
53-55 25 54 1.350
56-58 32 57 1.824
59-61 15 60 900
62-64 18 63 1.134
Jumlah 100 - 5.718
ΣFi.Xi 5.718
𝑥̅ = = = 57,18
ΣF 100
 Metode coding
Metode coding sering digunakan apabila nilai-nilai dalam data yang
berupa bilangan-bilangan besar. Pada dasarnya, metode itu merupakan
penjabaran dari metode simpangan rata-rata.

5. Dirumuskan :
ΣFu
𝑥̅ = M + C ( )
ΣF
Keterangan :
M = rata-rata hitung sementara
C = panjang kelas
u = 0, ± 1, ± 2, ...
=
𝑑
𝑐
, dengan d = X – M
Contoh soal:
Tabel 1. 1: Berat badan 100 orang mahasiswa
Berat
Badan (kg)
F X d= X - M u F.u
50-52 10 51 -2 -20
53-55 25 54 -3 -1 -25
56-58 32 57 0 0 0
59-61 15 60 3 1 15
62-64 18 63 6 2 36
Jumlah 100 - 0 0 6
ΣFu
𝑥̅ = M + C ( )
ΣF
6
𝑥̅ = 57 + 3 ( ) = 57, 18
100
2. Median (Me)
Median adalah nilai tengah dari data yang telah diurutkan. Median sering
juga disebut rata-rata posisi. Median disimbolkan dengan Me atau Md.

6. 1) Median data tunggal
 Jika jumlah data ganjil, mediannya adalah data yang berada paling
tengah.
Me = Xn/2
 Jika jumlah data genap, mediannya adalah hasil bagi jumlah dua data
yang berada di tengah.
xn + (n+2) / 2
2
Me =
2
Contoh 1:
Tentukan median dari data berikut!
3, 5, 4, 6, 8, 7, 3
Jawab :
Jumlah data = 7 (ganjil)
Data diurutkan akan menjadi seperti berikut:
3, 3, 4, 5, 6, 7, 8
Nilai 5 ada ditengah data yang telah diurutkan, maka 5
merupakan median.
2) Median data kelompok
Rumus:
Keterangan :
Lo = Tepi bawah kelas median
n = Banyaknya data
F = Frekuensi komulatif sebelum kelas median
F = Frekuensi kelas median
i = Interval / panjang kelas

7. Contoh :
Tentukan median dari distribusi frekuensi berikut:
Tabel 1.2 Diameter dari 40 buah pipa
Diameter Pipa (m) Frekuensi (F)
85-87 2
88-90 5
91-93 13
94-96 14
97-99 4
100-102 2
Jumlah 40
Penyelesaian :
Jumlah frekuensi (n) = 40 sehingga:
𝑛
2
= 20
Kelas median adalah (Σf2) ≥
𝑛
2
Sehingga: f1 + f2 + f3 = 20 ≥ 20
Jadi, kelas median adalah kelas : Ke-3
Kelas ke-3 yaitu: 91 – 93,
Maka: Lo = 90,5
i = 3
F = 7
f = 13
Sehingga median dari soal diatas adalah :
𝑛
2
- F
Me = Lo + i { }
f
= 90,5 + 3 {
20−7
13
}
Me = 93,5

8. 3. Modus (Mode)
Modus adalah nilai yang sering muncul dalam data. Modus disimbolkan dengan
Mo. Cara mencari modus dibedakan antara data tunggal dan data kelompok.
 Modus data tunggal
Modus data tunggal adalah data yang frekuensinya terbanyak.
Contoh :
Tentukan modus dari data : 1, 2, 4, 4, 5, 8, 9.
Modus = 4
 Modus data kelompok
Modus akan berada pada kelas yang memiliki frekuensi terbesar. Kelas yang
memiliki frekuensi terbesar disebut sebagai kelas modus.
Rumus :
Mo = Lo + i {
(𝒃𝟏)
(𝒃𝟏+𝒃𝟐)
}
Keterangan :
Lo = Tepi bawah dari kelas modus
i = Interval / panjang kelas
b1 = Beda frekuensi kelas modus dengan kelas modus sebelumnya
b2 = Beda frekuensi kelas modus dengan kelas modus sesudahnya
Contoh :
Tentukan modus dari distribusi frekuensi berikut :
Tabel 1.2 Diameter dari 40 buah pipa
Diameter Pipa (m) Frekuensi (f)
85-87 2
88-90 5
91-93 13
94-96 14
97-99 4
100-102 2
Jumlah 40

9. Dari soal diatas, diketahui :
Frekuensi terbesar yaitu: 14, yang berada pada kelas ke-4, yaitu: 94 – 96
Sehingga:
Lo = 93,5
i = 3
b1 = 14-13 = 1
b2 = 14-4 = 10
Mo = Lo + i {
(𝑏1)
(𝑏1+𝑏2)
}
= 93,5 + 3 {
(1)
(1+10)
}
= 93,5 + {
(1)
(11)
}
Mo = 96, 5
Contoh :
Carilah rata-rata, median dan modus dari tabel distribusi frekuensi berikut ini!
Hasil Tugas Frekuensi (fi)
65-67 2
68-70 5
71-73 13
74-76 14
77-79 4
80-82 2
Jumlah (Σ) 40
Jawab :
a) Rata-rata:
𝑥̅ =
𝛴𝑓𝑖𝑥𝑖
𝛴𝑓𝑖

10. Hasil Tugas Frekuensi (fi) Titik Tengah (Xi) fixi
65-67 2 66 132
68-70 5 69 345
71-73 13 72 936
74-76 14 75 1.050
77-79 4 78 312
80-82 2 81 162
Jumlah (Σ) 40 2.937
x̅ =
𝛴𝑓𝑖𝑥𝑖
𝛴𝑓𝑖
=
2.937
40
= 7.343
b) Median :
𝑛
2
− F
Me = Lo + i{ f }
Median = nilai tengah sehingga :
𝑛
2
=
40
2
= 20 (berada pada frekuensi
komulatif di kelas ke-3),
Sehingga:
Type equation here. Lo = 70, 5
i = 3
F = 7
f = 13
𝑛
2
- F
Me = Lo + i { f }
40
2
- 7
Me = 70,5 + 3{ 13 }
= 70, 5 + 3 {
13
13
}
Me = 73, 5
c) Modus (Mo)
Mo = Lo + i {
(𝑏1)
( 𝑏1+𝑏2)
}

11. Modus = nilai yang sering muncul atau paling besar frekuensinya. Dari tabel
diatas frekuensi terbesar = 14, berada pada kelas ke-4,
Sehingga :
Lo = 73,5
i = 3
b1 = 14 – 13 = 1
b2 = 14 – 4 = 10
Mo = 73,5 + 3 {
1
(1+10)
}
Mo = 73, 5 + 3 {
1
11
}
Mo = 73,5 +
3
11
Mo = 73,5 + 0,3
Mo = 73,8
Contoh rata-rata hitung (mean) data kelompok
Batas kelas Frekuensi (F) Nilai tengah (Xi)
40-44 25 42
45-49 10 47
50-54 5 52
55-59 8 57
60-64 2 62
Jumlah 50 3450
Carilah rata-rata , median dan modus dari tabel diatas !
Rata-rata
𝑋̅ =
∑𝐹𝑖.𝑋𝑖
𝐹
=
3450
50
=69

12. Median
𝑛
2
=
50
2
= 25 terdapat pada kelas ke 1 (40-44), sehingga :
Lo = 39.5
I = 5
F = 25
f = 25
Me = Lo + i {
𝑛
2
−𝐹
𝑓
}
= 39,5 + 5 {
50−25
25
}
= 39,5 + 5 {
25
25
}
= 44,5
Modus
Mo = Lo + i {
(b1)
(b1+b2)
, sehingga :
Lo = 39,5
I = 5
B1= 25-0 =25
B2 = 25-10= 15
Mo = 39,5+ 5 {
25
25+15
}
= 39,5 + 5 {
25
40
}
= 39,5 + 3,125
= 42,625