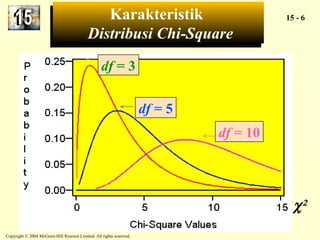
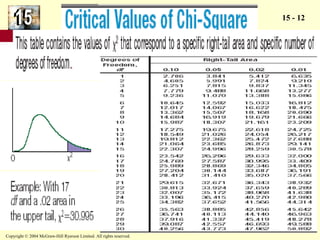
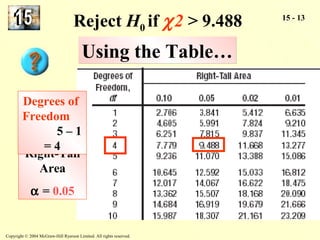
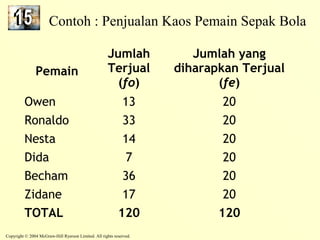
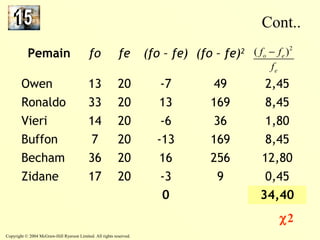
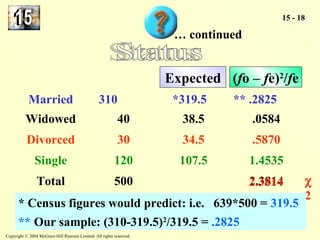
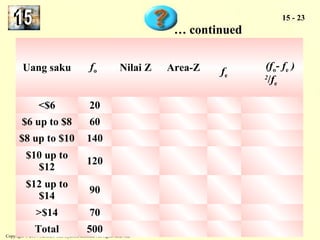
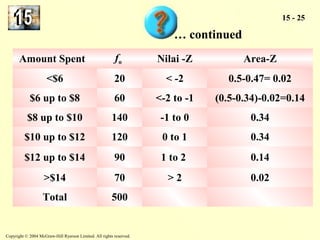
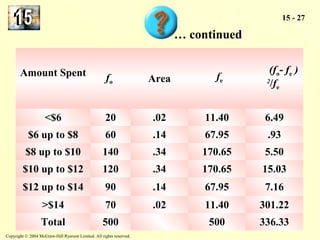
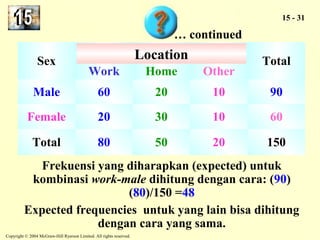
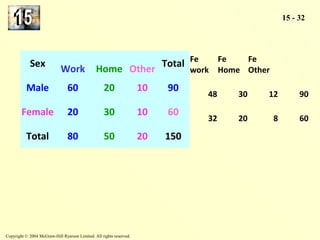
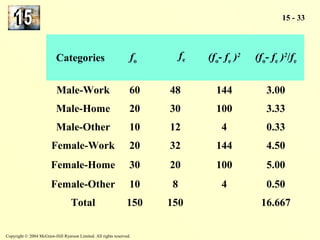
The document discusses the chi-square distribution and its various uses. It explains that the chi-square distribution is used to test hypotheses comparing observed versus expected frequency distributions, test hypotheses of normality, and determine if two attributes are independent using a contingency table. Examples are provided for goodness-of-fit tests, normality tests, and tests of independence.

1. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 1

2. When you have completed this chapter, you will be able to:
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 2
Understand the nature and role of
chi-square distribution
Identify a wide variety of uses of
the chi-square distribution
Conduct a test of hypothesis comparing an
observed frequency distribution to an
expected frequency distribution

3. Conduct a test of hypothesis for normality
using the chi-square distribution
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 3
Conduct a hypothesis test to determine
whether two attributes are
independent

4. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 4
Sebelumnya:
• skala pengukuran data: interval atau rasio
• pengujian rata-rata, proporsi, varians populasi
• mengasumsikan populasi mengikuti distribusi normal
Metode Parametrik
Sekarang, bagaimana dengan:
• data skala pengukuran: nominal atau ordinal
• asumsi tidak ada pada bentuk distribusi populasi
Metode Non Parametrik
Salah satu Metode Non Parametrik: Chi Square (c2 )

5. Karakteristik
Karakteristik 15 - 5
Distribusi Chi-Square
Distribusi Chi-Square
… Menceng/menjulur ke kanan (positively
skewed)
… non-negatif
… berdasarkan degrees of freedom
… Ketika degrees of freedom berubah maka
distribusi baru akan terbentuk
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
…e.g.

6. Karakteristik
Distribusi Chi-Square
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 6
df = 3
df = 5
df = 10
c2
Karakteristik
Distribusi Chi-Square

7. • Uji Chi-square digunakan untuk:
1. Menguji apakah frekuensi aktual sama
dengan frekuensi yang diharapkan (berasal
dari distribusi populasi yang dihipotesiskan).
2. Menentukan apakah sampel pengamatan
berasal dari distribusi tertentu yang
berdistribusi normal
3. Analisis tabel kontinjensi, digunakan untuk
menguji apakah dua sifat atau karakteristik
saling berkaitan (Uji Independensi)
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.

8. Goodness-of-Fit Test:
15 - 8 Goodness-of-Fit Test:
Equal Expected
Frequencies
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
Equal Expected
Frequencies
f0: frekuensi observasi (observed)
fe : frekuensi yang diharapkan (expected)
H0: Tidak ada perbedaan antara frekuensi
observasi (observed) dan yang diharapkan
(expected).
H1: Ada perbedaan antara frekuensi
observasi (observed) dan yang diharapkan
(expected).

9. Goodness-of-Fit Test:
Goodness-of-Fit Test:
Equal Expected
Frequencies
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 9
Equal Expected
Frequencies
å ( ) ê êë
é -
=
f f 2
o e
…Nilai kritis: nilai chi-square dengan
degrees of freedom: k-1 ,
di mana k adalah jumlah kategori
e
f
c 2
ê êë
é
… Uji statistik:

10. Goodness-of-Fit Test:
Goodness-of-Fit Test:
Equal Expected
Frequencies
Equal Expected
Frequencies
Hari Frekuensi
Senin 120
Selasa 45
Rabu 60
Kamis 90
Jumat 130
TOTAL 445
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 10
Informasi berikut menunjukkan jumlah karyawan
yang absen setiap hari dalam seminggu di sebuah pabrik.
Hari Frekuensi
Senin 120
Selasa 45
Rabu 60
Kamis 90
Jumat 130
TOTAL 445
Pada tingkat signifikansi 0.05, apakah ada
perbedaan jumlah absensi per hari dalam
seminggu tersebut?

11. Goodness-of-Fit Test:
Goodness-of-Fit Test:
Equal Expected
Frequencies
Equal Expected
Frequencies
(120+45+60+90+130)/5 = 89
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 11
H Hyyppootthheessisis T Teesstt
SStteepp 11
SStteepp 22
SStteepp 33
SStteepp 44
H: Tidak ada perbedaan tingkat absensi per
0hari dalam seminggu tersebut…
H: Tingkat absensi per hari tidak semua sama
1a = 0.05
Use Chi-Square test
Degrees of freedom (5-1) = 4
Tolak Hjika c 2 >
0 9.488 (dari tabel Chi-square)
Chi-Square

12. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 12

13. Reject H0 if c 2 > 9.488
UUssiinngg tthhee TTaabbllee……
Degrees of
Freedom
5 – 1
= 4
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 13
Right-Tail
Area
a = 0.05

14. å( é f o úû
ú -
f ) 2
ù
e
f
Hari Frekuensi Expected (fo – fe)2/fe
Senin 120 89 10.80
Selasa 45 89 21.75
Rabu 60 89 9.45
Kamis 90 89 0.01
Jumat 130 89 18.89
Total 445 445 60.90
Hari Frekuensi Expected (fo – fe)2/fe
Senin 120 89 10.80
Selasa 45 89 21.75
Rabu 60 89 9.45
Kamis 90 89 0.01
Jumat 130 89 18.89
Total 445 445 60.90
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 14
== 11..9988
ê êë
=
e
c2
c2
Kesimpulan: Hypothesis Nol (H0) ditolak.
Tingkat ansensi tidak sama pada tiap hari dalam seminggu
tersebut.
(120-89)2/89
SStteepp 55
Tes Statistik
Reject H0 if c 2 > 9.488

15. Contoh : Penjualan Kaos Pemain Sepak Bola
Pemain
Jumlah
Terjual
(fo)
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
Jumlah yang
diharapkan Terjual
(fe)
Owen 13 20
Ronaldo 33 20
Nesta 14 20
Dida 7 20
Becham 36 20
Zidane 17 20
TOTAL 120 120

16. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
Cont..
Pemain fo fe (fo – fe) (fo – fe)2
( )2 o e
f -
f
f
e
Owen 13 20 -7 49 2,45
Ronaldo 33 20 13 169 8,45
Vieri 14 20 -6 36 1,80
Buffon 7 20 -13 169 8,45
Becham 36 20 16 256 12,80
Zidane 17 20 -3 9 0,45
0 34,40
c2

17. Data Biro Sensus Amerika menunjukkan bahwa di Amerika Serikat:
Married Widowed Divorced Single
63.9% 7.7% 6.9% 21.5%
Sample 500 orang dewasa dari Philadelphia menunjukkan:
310 40 30 120
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 17
Not re-married Never married
Pada tingkat signifikansi 0.05, dapatkah disimpulkan
bahwa area Philadelphia berbeda dengan Amerika
Serikat secara keseluruahan?

18. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 18
… continued
Expected (fo – fe)2/fe
Married 310 *319.5 ** .2825
Widowed 40 38.5 .0584
Divorced 30 34.5 .5870
Single 120 107.5 1.4535
Total 500 2.3814
c2
* Census figures would predict: i.e. 639*500 = 319.5
** Our sample: (310-319.5)2/319.5 = .2825

19. a = 0.05
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 19
SStteepp 11
SStteepp 22
SStteepp 33
SStteepp 44
… continued
H0: The distribution has not changed
H1: The distribution has changed.
H0 is rejected if
c2 >7.815, df = 3
c2 = 2.3814
Reject the null hypothesis.
The distribution regarding marital status in Philadelphia
is different from the rest of the United States.

20. Goodness-of-Fit Test:
Equal Expected Frequencies
• Contoh :
Dosen mengharapkan distribusi nilai ujian : A
= 40%, B = 40%, dan C = 20%. Hasil ujian
menunjukkan distribusi nilai sebagai berikut :
A : 30 orang B : 20 orang C : 10 orang
Uji dengan level of significance 10%, apakah
distribusi nilai tersebut sesuai dengan harapan
dosen tersebut ?
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.

21. Goodness-of-Fit Test:
Goodness-of-Fit Test: 15 - 21
…untuk menentukan rata-rata dan standar deviasi
distribusi frekuensi
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
Normality
Normality
… tes ini menguji
apakah frekuensi aktual (observed)
pada sebuah distribusi frekuensi sesuai dengan
distribusi normal.
(1) Hitung nilai-z untuk batas bawah kelas dan
batas atas kelas pada tiap kelas
(2) Tentukan fe untuk setiap kategori.
(3) Gunakan uji chi-square (goodness-of-fit test)
untuk menentukan apakah fo sesuai dengan fe

22. Goodness-of-Fit Test:
Goodness-of-Fit Test:
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 22
Normality
Normality
Sampel uang saku 500 siswa dilaporkan dalam
distribusi frekuensi berikut ini
Apakah dapat disimpulkan bahwa distribusinya
normal dengan rata-rata $10 dan standar deviasi $2?
 Gunakan tingkat signifikansi 0.05

23. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 23
Uang saku fo Nilai Z Area-Z
fe
(fo- fe )
2/fe
<$6 20
$6 up to $8 60
$8 up to $10 140
$10 up to
$12 120
$12 up to
$14 90
>$14 70
Total 500
… continued

24. z X -
m
=
s
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 24
… continued
To compute fe for the first class,
first
determine the -
z - value
6 10 = -
2
=
Now…
2 . 00
find the probability of a z - value less than –2.00
P(z < -2.00) = 0.5000-.4772= .0228

25. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 25
… continued
Amount Spent fo Nilai -Z Area-Z
<$6 20 < -2 0.5-0.47= 0.02
$6 up to $8 60 <-2 to -1 (0.5-0.34)-0.02=0.14
$8 up to $10 140 -1 to 0 0.34
$10 up to $12 120 0 to 1 0.34
$12 up to $14 90 1 to 2 0.14
>$14 70 > 2 0.02
Total 500

26. f e = (.0228 )(500 ) = 11 .40
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 26
… continued
The expected frequency is the probability of a
z-value less than –2.00 times the sample size
The other expected frequencies
are computed similarly

27. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 27
Amount Spent
fo Area
… continued
fe
(fo- fe )
2/fe
<$6 20 .02 11.40 6.49
$6 up to $8 60 .14 67.95 .93
$8 up to $10 140 .34 170.65 5.50
$10 up to $12 120 .34 170.65 15.03
$12 up to $14 90 .14 67.95 7.16
>$14 70 .02 11.40 301.22
Total 500 500 336.33

28. H0: The observations do NOT follow the normal
a = 0.05
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 28
… continued
SStteepp 11
SStteepp 22
SStteepp 33
SStteepp 44
H0: The observations follow the normal distribution
distribution
H0 is rejected if c2 >7.815, df = 6
c2 = 336.33
H0: is rejected.
The observations do NOT follow the normal distribution

29. Tabel kontinjensi digunakan untuk analisis
apakah dua sifat atau karakteristik
… masing-masing observasi dikelompokkan berdasarkan dua kriteria
…Menggunakan prosedur uji hipothesis biasa
… degrees of freedom :
(jumlah baris -1)(jumlah kolom -1)
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 29
Tabel kontinjensi digunakan untuk analisis
apakah dua sifat atau karakteristik
saling berkaitan
saling berkaitan
… Frekuensi yang diharapkan (expected)
dihitung dengan cara:
Expected Frequency = (Total baris)(Total kolom)/grand total

30. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 30
Apakah ada hubungan antara lokasi
kecelakaan dan jenis kelamin orang
yang terlibat dalam kecelakaan itu?
Sampel 150 kecelakaan yang dilaporkan
ke polisi dikelompokkan berdasarkan
lokasi dan jenis kelamin.
Pada tingkat signifikansi 0.05, dapatkah
disimpulkan bahwa jenis kelamin dan
lokasi kecelakaan saling berhubungan?

31. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 31
… continued
Sex
Location
Work Home Other
Total
Male 60 20 10 90
Female 20 30 10 60
Total 80 50 20 150
Frekuensi yang diharapkan (expected) untuk
kombinasi work-male dihitung dengan cara: (90)
(80)/150 =48
Expected frequencies untuk yang lain bisa dihitung
dengan cara yang sama.

32. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 32
Sex Work Home Other Total Fe
work
Fe
Home
Fe
Other
Male 60 20 10 90
48 30 12 90
Female 20 30 10 60
32 20 8 60
Total 80 50 20 150

33. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 33
Categories fo
fe
(fo- fe )2 (fo- fe )2/fe
Male-Work 60 48 144 3.00
Male-Home 20 30 100 3.33
Male-Other 10 12 4 0.33
Female-Work 20 32 144 4.50
Female-Home 30 20 100 5.00
Female-Other 10 8 4 0.50
Total 150 150 16.667

34. H0: The Gender and Location are related
a = 0.05
(…there are (3- 1)(2-1) = 2 degrees of freedom)
Find the value of c 2
( ) ( )
60 48 2 2
c 2 = - + + -
... 10 8
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 34
SStteepp 11
SStteepp 22
SStteepp 33
SStteepp 44
H0: The Gender and Location are NOT related
H0 is rejected if c 2 >5.991, df = 2
8
H0: is rejected.
Gender and Location are related!
48
… continued
= 16 .667

35. Latihan 1:
Equal Expected Frequencies
Dosen mengharapkan distribusi nilai ujian : A
= 40%, B = 40%, dan C = 20%. Hasil ujian
menunjukkan distribusi nilai sebagai berikut :
A : 30 orang B : 20 orang C : 10 orang
Uji dengan level of significance 10%, apakah
distribusi nilai tersebut sesuai dengan harapan
dosen tersebut ?
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.

36. Latihan 2:
Manajer produksi meneliti tingkat kerusakan pada
mesin produksi. Hasilnya pengamatan terhadap barang
yang diproduksi sebagai berikut
Kondisi Mesin 1 Mesin 2 Mesin 3
Rusak 12 15 6
Baik 88 105 74
Apakah kerusakan tersebut disebabkan mesin atau
kebetulan saja ? Uji dengan a = 0,05
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.

37. Latihan 3:
Lembaga riset meneliti apakah ada hubungan
antara jenis surat kabar yang dibaca dengan
kelompok masyarakat. Hasilnya sebagai berikut :
Uji dengan a = 0,1
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
Surat Kabar
Kelompok A B C
Atas 170 124 90
Menengah 120 112 100
Bawah 130 90 88

38. TTeesstt yyoouurr lleeaarrnniinngg…… 15 - 38
Click on… Click on…
www.mcgrawhill.ca/college/lind
Online Learning Centre
for quizzes
extra content
data sets
searchable glossary
access to Statistics Canada’s E-Stat data
…and much more!
Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.

39. Copyright © 2004 McGraw-Hill Ryerson Limited. All rights reserved.
15 - 39
TThhisis c coommppleletetess C Chhaappteterr 1 155