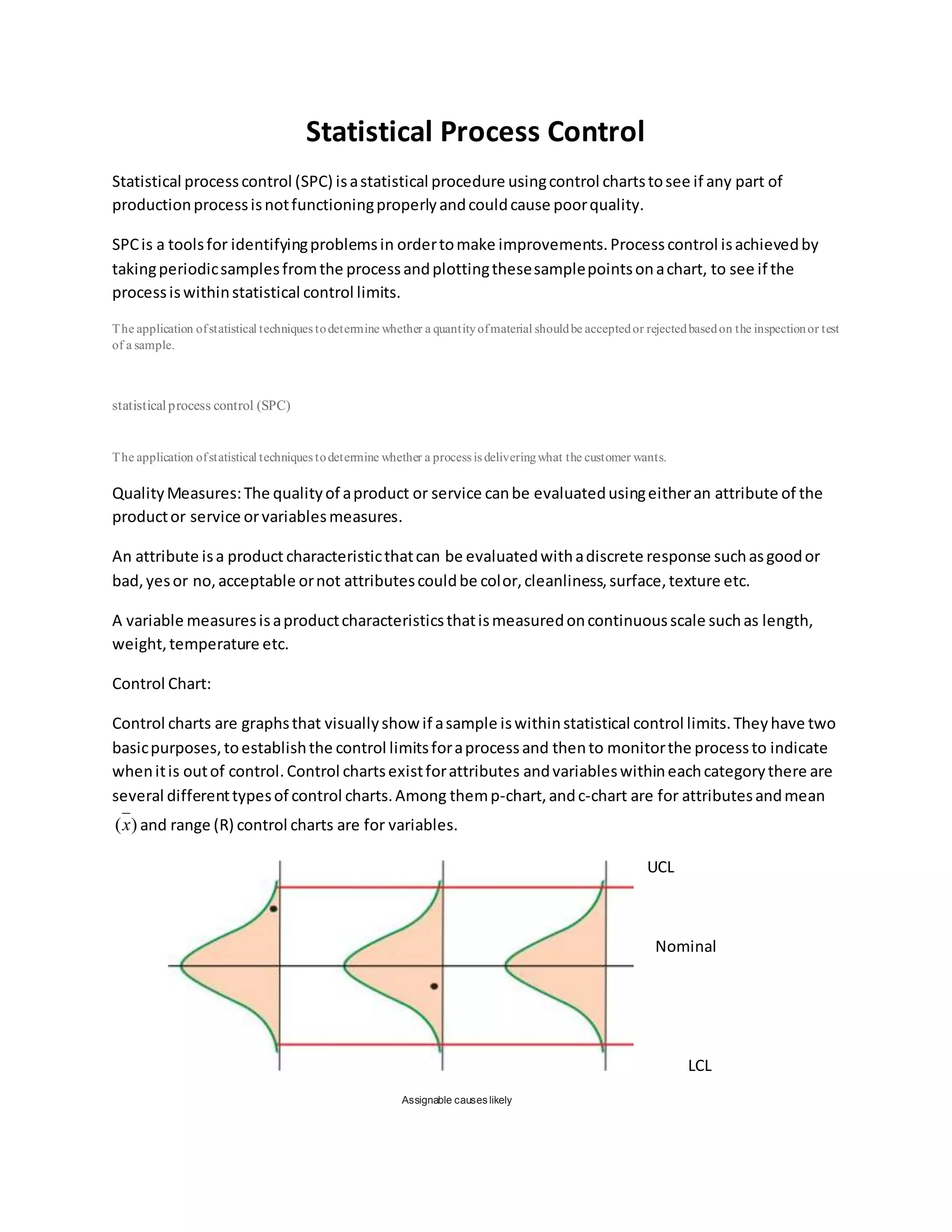
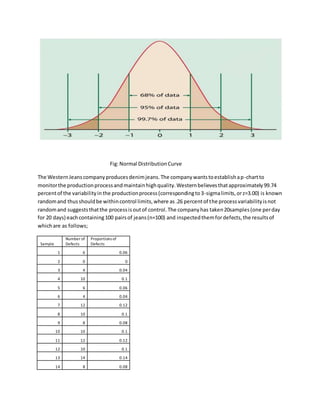
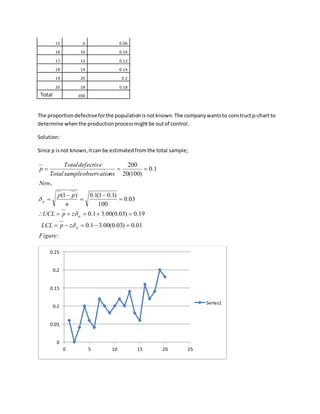
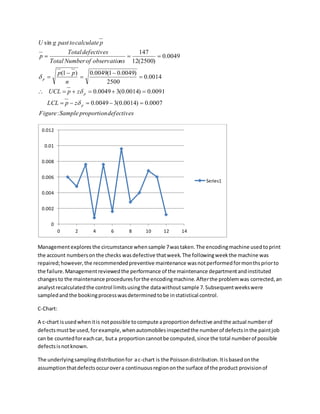
The document discusses statistical process control (SPC) and various quality control charts used to monitor processes and identify sources of variation. It provides information on: 1) SPC uses control charts to monitor key process parameters and determine whether the production process is functioning properly or causing poor quality. 2) Control charts have limits calculated from sample data that indicate whether the process is in or out of statistical control. Different charts exist for attributes and variables. 3) Examples show how to construct p-charts and c-charts from sample data and determine if the process is within control limits based on the samples.

1. Statistical Process Control
Statistical processcontrol (SPC) isastatistical procedure usingcontrol chartstosee if any part of
productionprocessisnotfunctioningproperlyandcouldcause poorquality.
SPCis a toolsfor identifyingproblemsin ordertomake improvements.Processcontrol isachievedby
takingperiodicsamplesfromthe processandplottingthesesamplepointsonachart, to see if the
processiswithinstatistical control limits.
The application ofstatistical techniques todetermine whether a quantityofmaterial shouldbe acceptedor rejectedbasedon the inspectionor test
of a sample.
statisticalprocess control (SPC)
The application ofstatistical techniques todetermine whether a process is deliveringwhat the customer wants.
QualityMeasures:The qualityof aproduct or service canbe evaluatedusingeitheran attribute of the
productor service orvariablesmeasures.
An attribute isa product characteristicthatcan be evaluatedwithadiscrete response suchasgoodor
bad,yesor no,acceptable ornot attributescouldbe color,cleanliness,surface,texture etc.
A variable measuresisaproductcharacteristicsthatismeasuredoncontinuousscale suchas length,
weight,temperature etc.
Control Chart:
Control charts are graphsthat visuallyshow if asample iswithinstatistical control limits.Theyhave two
basicpurposes,toestablishthe control limitsforaprocessand thento monitorthe processto indicate
whenitis outof control.Control chartsexistforattributes andvariableswithineachcategorythere are
several differenttypesof control charts.Among themp-chart,andc-chart are for attributesandmean
)(x and range (R) control charts are for variables.
UCL
Nominal
LCL
Assignable causes likely

2. ControlCharts for Attributes
Two charts commonlyused for performance measures based on attributes measures are the p- and c-chart. The p-
chart is used for controlling the proportion of defects generated by the process.The c-chart is used for controlling the
number of defects when more than one defect can be present in a service or product.
p-chart
A chart used for controlling the proportion of defective services or products generated by the process.
p-Charts The p-chart is a commonlyused control chart for attributes. The performance char-acteristic is counted
rather than measured,and the entire service or item can be declared good or defective. For example, in the banking
industry, the attributes counted might be the number of nonendorsed deposits or the number of incorrect financial
statements sent to customers. The method involves selecting a random sample, inspecting each item in it, and
calculating the sam-ple proportion defective, p, which is the number of defective units divided by the sample size.
Sampling for a p-chart involves a “yes/no” decision: The process output either is or is not defective. The
underlying statistical distribution is based on the binomial distribution. However, for large sample sizes, the no rmal
distributionprovides a good approximation to it. The standard deviation of the distribution of proportion defectives, s p,
is
sp = npp /)1( 
where
n = sample size
= central line on the chart, which can be either the historical average population
proportion defective or a target value
We can use sp to arrive at the upper and lower control limits for a p-chart:
UCLp = p + z sp and LCLp = p - z sp
where
z = normal deviate (number ofstandard deviations from the average)
Z is occasionallyequal to 2.00 but mostfrequently is 3.00. A Z values of 2.00 corresponds to an overall normal
probability of 95 percent and z=3.00 corresponds to a normal probabilityof 99.74 percent. Managementusually
selects z=3.00 because ifthe process is in control ifwants a high probabilitythat the sample values will fall within the
control limits.

3. Fig:Normal DistributionCurve
The WesternJeanscompanyproducesdenimjeans.The companywantstoestablishap-chartto
monitorthe productionprocessandmaintainhighquality.Westernbelievesthatapproximately99.74
percentof the variabilityinthe productionprocess(correspondingto3-sigmalimits,orz=3.00) is known
randomand thusshouldbe withincontrol limits,where as.26 percentof the processvariabilityisnot
randomand suggeststhatthe processisoutof control.The companyhas taken20samples(one perday
for 20 days) eachcontaining100 pairsof jeans(n=100) and inspectedthemfordefects,the resultsof
whichare as follows;
Sample
Number of
Defects
Proportions of
Defects
1 6 0.06
2 0 0
3 4 0.04
4 10 0.1
5 6 0.06
6 4 0.04
7 12 0.12
8 10 0.1
9 8 0.08
10 10 0.1
11 12 0.12
12 10 0.1
13 14 0.14
14 8 0.08

4. 15 6 0.06
16 16 0.16
17 12 0.12
18 14 0.14
19 20 0.2
20 18 0.18
Total 200
The proportiondefectiveforthe populationisnotknown.The companywantsto constructp-chart to
determine whenthe productionprocessmightbe outof control.
Solution:
Since p isnot known,itcan be estimatedfromthe total sample;
:
01.0)03.0(00.31.0
19.0)03.0(00.31.0
03.0
100
)1.01(1.0)1(
,
1.0
)100(20
200
Figure
zpLCL
zpUCL
n
pp
Now
nsobservatiosampleTotal
defectiveTotal
p
p
p
p











0
0.05
0.1
0.15
0.2
0.25
0 5 10 15 20 25
Series1

5. The processis belowthe lowercontrol limitsforsample 2(i,e duringday2).
The above processwas the upperlimitsduringday19.
Example-2:The operationmanagerof the bookingservicesdepartmentof hometownbankisconcerned
aboutthe numberof wrongcustomer account numbersrecordedbyhometownpersonnel.Eachweeka
randomsample of 2500 depositsistakenandthe numberincorrectaccountnumbersrecorded.The
resultsforthe past 12 weeksare showninthe followingtable.Isthe bookingprocessoutof statistical
control?Use three sigmacontrol limits.
Sample Number Wrong account Number Proportionsof Defects
1 15 0.006
2 12 0.0048
3 19 0.0076
4 2 0.0008
5 19 0.0076
6 4 0.0016
7 24 0.0096
8 7 0.0028
9 10 0.004
10 17 0.0068
11 15 0.006
12 3 0.0012
Solution:

6. defectivesproportionSampleFigure
zpLCL
zpUCL
n
pp
nsobservatioofNumberTotal
defectivesTotal
p
pcalculatetopastgU
p
p
p
:
0007.0)0014.0(30049.0
0091.0)0014.0(30049.0
0014.0
2500
)0049.01(0049.0)1(
0049.0
)2500(12
147
sin











Managementexplores the circumstance whensample 7wastaken.The encodingmachine usedtoprint
the account numbersonthe checks wasdefective thatweek.The followingweekthe machine was
repaired;however,the recommendedpreventive maintenance wasnotperformedformonthspriorto
the failure.Managementreviewedthe performance of the maintenance departmentandinstituted
changesto the maintenance proceduresforthe encodingmachine.Afterthe problemwas corrected,an
analystrecalculatedthe control limitsusingthe datawithoutsample 7.Subsequentweekswere
sampledandthe bookingprocesswasdeterminedtobe instatistical control.
C-Chart:
A c-chart isusedwhenitis notpossible tocompute aproportiondefective andthe actual numberof
defectsmustbe used,forexample,whenautomobilesinspectedthe numberof defectsinthe paintjob
can be countedforeachcar, buta proportioncannotbe computed,since the total numberof possible
defectsisnotknown.
The underlyingsamplingdistributionfor ac-chart is the Poissondistribution.Itisbasedonthe
assumptionthatdefectsoccurovera continuousregiononthe surface of the product provisionof
0
0.002
0.004
0.006
0.008
0.01
0.012
0 2 4 6 8 10 12 14
Series1

7. service andthat the probabilityonthe surface orat any instantof time isnegligible.The meanof the
distributionis c andstandarddeviationis c .
The control limitsare;
c
c
zcczcLCL
zcczcUCL




Exercise-1:The Ritzhotel has240 rooms.The hotel’shousekeepingdepartmentisresponsiblefor
maintainingthe qualityof the rooms’appearance andcleanliness.Eachindividual housekeeperis
responsible foranarea encompassing20rooms.Everyroom inuse is thoroughlycleanedandits
supplies,toiletriesandsoonare restockedeachday.Anydefectsthatthe housekeeping staffsnotice
that are notpart of the normal housekeepingservice are supposedtobe reportedtohotel
maintenance.Everyroomisbrieflyinspectedeachdaybya housekeeping supervisor.However,hotel
managementalsoconductsinspectiontoursatrandomfor detailedthroughinspectionforquality
control purposes.The housekeepingservice defectslike aninoperativeormissingTV remote,poorTV
picture qualityorreceptiondefective lamps,amalfunctioningclock,tearsorstainsinthe bedcoveror
curtainsor a malfunctioningcurtainpull.Aninspectionsampleincludes12roomsi,e one room selected
at random fromeach of the twelve 20 roomblocksservicedbya house keeper.Followingare the results
from15 inspection samplesconductedatrandomduringa one monthperiod.
Sample
No.of
Defects Sample
No.of
Defects
1 12 8 14
2 8 9 13
3 16 10 15
4 14 11 12
5 10 12 10
6 11 13 14
7 9 14 17
15 15
The hotel believesthatapproximately99percentof the defects(correspondingto3 sigmalimits) are
causedby nonrandomvariability.Theywanttoconstructa c-chart tomonitorthe housekeepingservice
Solution:
The populationprocessaverage isnotknown,the sample estimate, c ,can be usedinstead

8. 99.167.12367.12
35.2367.12367.12
00.3sinlim
67.12
15
190




czczcLCL
czczcUCL
followaszgucomputedareitscontrolThe
c
c
c


Figure:
All the sample observationsare withinthe control limits.Suggestingthatthe roomqualityisincontrol.
Exercise-2:
The woodlandpapercompanyproducespaperforthe newspaperindustry.Asafinal stepinthe process,
the paperpassesthrougha machine that measuresvariousproductqualitycharacteristicswhenthe
paperproductionprocessisincontrol it averages20 defectsperroll.
a) Setup control chart for the numberof defectsperroll use 2 sigmacontrol limits.
b) Five rollshadthe followingnumberof defects:16,21, 17, 22, 21 and 24 respectively.The sixth
roll usingpulpfroma differentsupplierhad5 defects.Isthe paperproductionprocessis
control?
Solution:
a) The average numberof defectsperroll is20 , therefore
0
2
4
6
8
10
12
14
16
18
0 5 10 15 20
Series1

9. 06.1120220
94.2820220


czcLCL
czcUCL
Figure:
The supplierforthe first5 sampleshasbeenusedbywoodlandpaperfor manyyears.The
supplierforthe sixthsample isnew tothe company.Managementdecidedtocontinue usingthe
newsupplierforawhile,monitoringthe numberof defectstosee if itstayslow.If the number
remainsbelowthe lcl for20 consecutive samples, managementwill make the switchpermanent
and recalculate the control chartparameter.
0
5
10
15
20
25
30
0 1 2 3 4 5 6 7
Series1