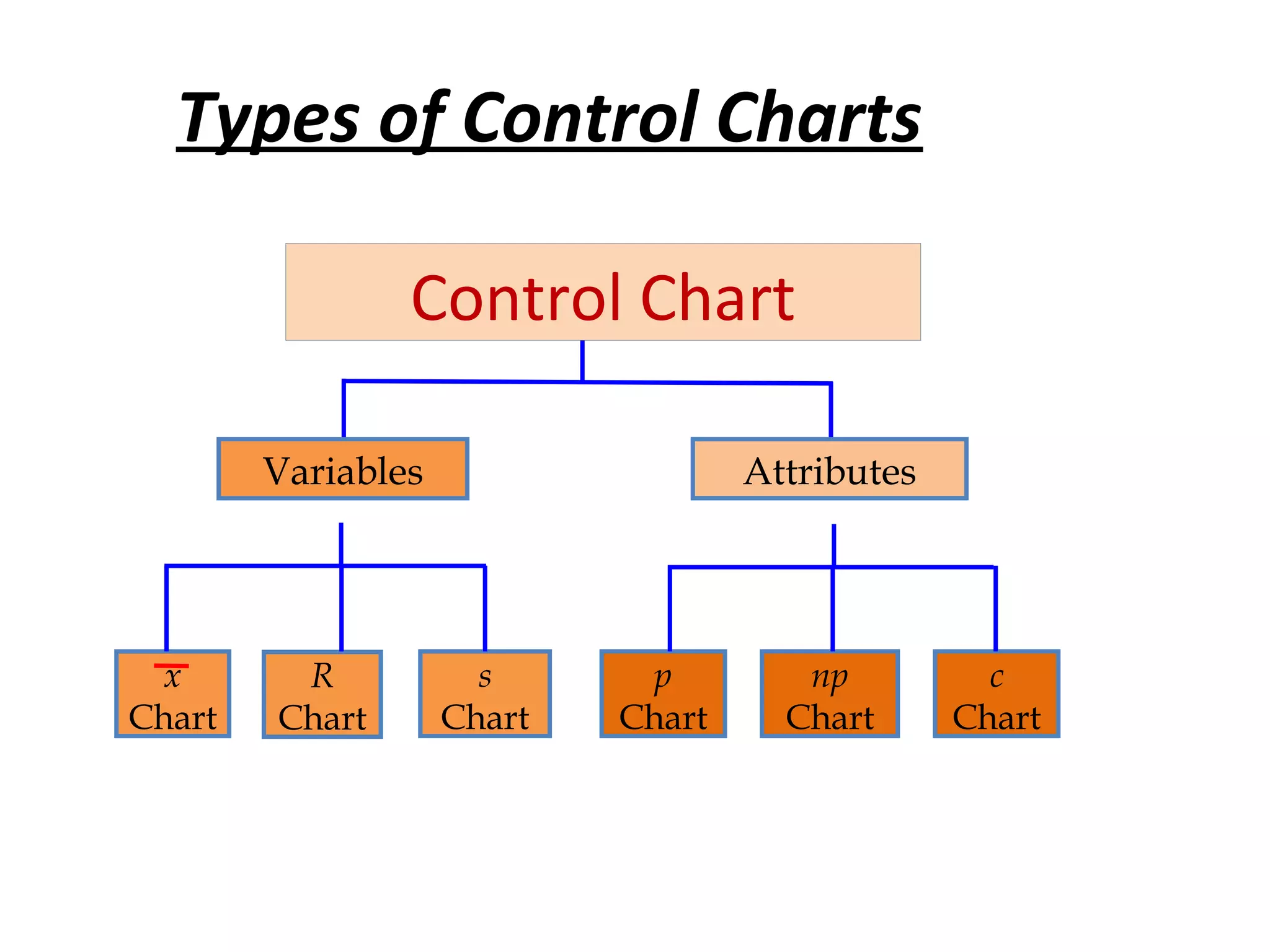
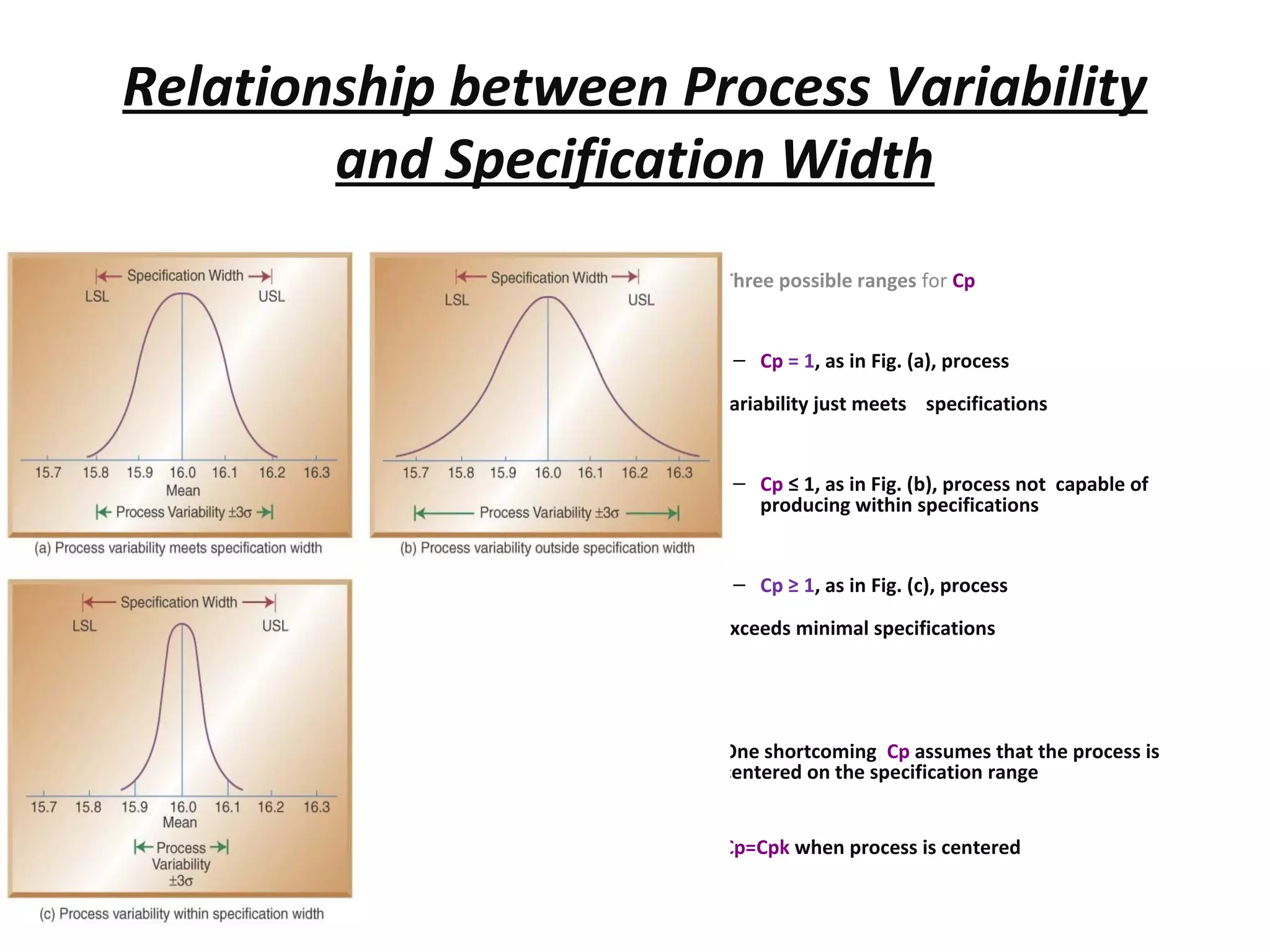
Quality is defined as customers' perception of how well a product or service meets their expectations. There are three types of quality: quality of design, quality of performance, and quality of conformance. Statistical quality control uses statistical techniques to control, improve, and maintain quality. Control charts are used to determine if a process is in or out of control by monitoring for random or assignable variation. Process capability indices like Cp and Cpk compare process variability to specification limits to determine if a process is capable of meeting specifications.