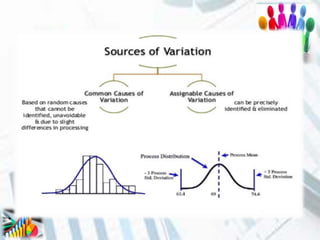
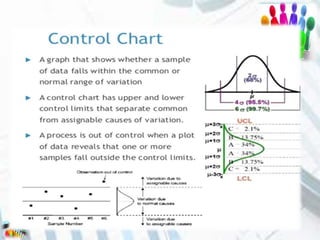
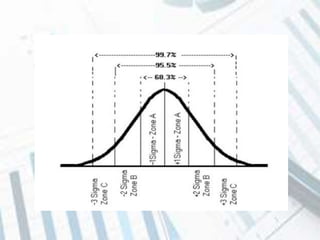
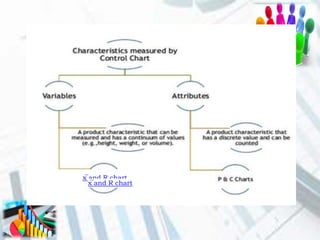
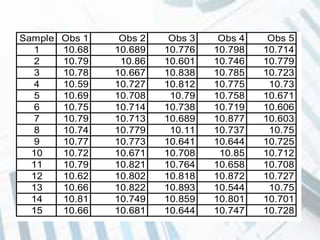
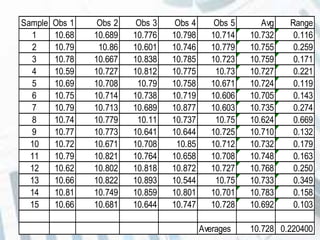
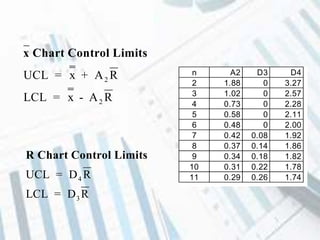
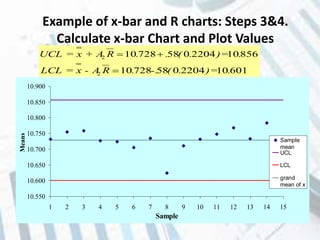
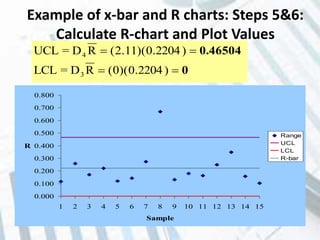
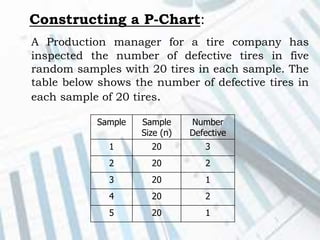
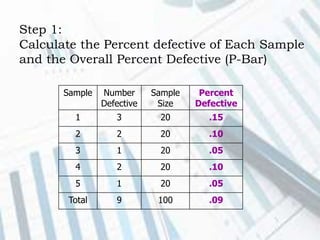
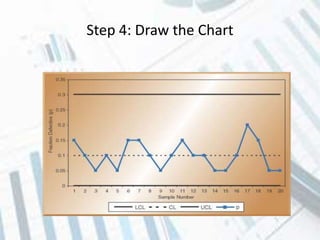
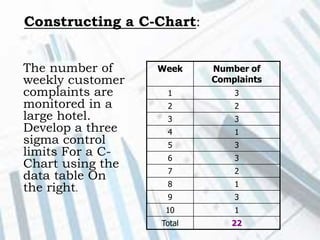
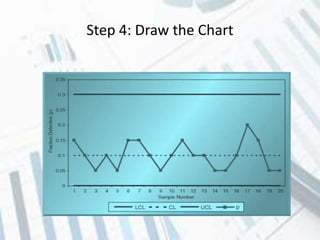
The document discusses quality control and statistical quality control. It defines quality as properties valued by consumers and quality control as maintaining standards through testing samples. The goal of quality control is to eliminate nonconformities and wasted resources at lowest cost. Statistical quality control uses statistical tools like descriptive statistics, acceptance sampling, and statistical process control to measure and control variation in processes. Examples are provided of x-bar and R charts to determine if a gluing process is in control, as well as P and C charts to monitor defects and complaints.

2. The word "Quality" represents the
properties of products and/or
services that are valued by the
consumer.

3. A system of maintaining standards
in manufactured products by
testing a sample of the output
against the specification.

4. In each process, excessive variations and errors can
cause nonconformities, which leads to three
undesirable consequences:
 scrapped or wasted resources;
 degraded process throughput;
 “contamination” from undetected
nonconformities,
 reducing the value of the product to the customer
NEED OF QUALITY CONTROL

5. GOAL OF QUALITY CONTROL
The goal of quality control in every production
system is to
 eliminate nonconformities and their consequences,
 eliminate rework and wasted resources, and
 achieve these goals at the lowest possible cost

7. A branch of mathematics used to
summarize, analyze, and
interpret a group of numbers or
observations.

8. Statistical quality control (SQC) is
the term used to describe the
set of statistical tools used by
quality professionals.

10.  Descriptive Statistics used to describe quality
characteristics and relationships
 Acceptance Sampling The process of randomly inspecting a
sample of goods and deciding whether to accept the entire lot
based on the results
 Statistical Process Control (SPC) A statistical tool that
involves inspecting a random sample of output from a process
and deciding whether the process is producing products with
the characteristics that fall within a predetermined range.

11. Why SPC is the Most Important Tool of
the SQC?
Measure the value of a quality characteristic
Help to identify a change or variation in some
quality characteristic of the product or process

12. Some Information about SPC
 SPC can be applied to any process.
 There is inherent variation in any process which can be
measured and “controlled”.
 SPC doesn’t eliminate variation, but it does allow the user to
track special cause variation.
 “SPC is a statistical method of separating variation resulting
from special causes from natural variation and to establish
and maintain consistency in the process, enabling process
improvement.”

17. x̅ and R chart
x̅ and R chart

18. x̅ and R chart

20. The following collection of data
represents samples of the amount of
force applied in a gluing process:
Determine if the process is in control
by calculating the appropriate upper
and lower
control limits of the X-bar and R charts.

21. Sample Obs 1 Obs 2 Obs 3 Obs 4 Obs 5
1 10.68 10.689 10.776 10.798 10.714
2 10.79 10.86 10.601 10.746 10.779
3 10.78 10.667 10.838 10.785 10.723
4 10.59 10.727 10.812 10.775 10.73
5 10.69 10.708 10.79 10.758 10.671
6 10.75 10.714 10.738 10.719 10.606
7 10.79 10.713 10.689 10.877 10.603
8 10.74 10.779 10.11 10.737 10.75
9 10.77 10.773 10.641 10.644 10.725
10 10.72 10.671 10.708 10.85 10.712
11 10.79 10.821 10.764 10.658 10.708
12 10.62 10.802 10.818 10.872 10.727
13 10.66 10.822 10.893 10.544 10.75
14 10.81 10.749 10.859 10.801 10.701
15 10.66 10.681 10.644 10.747 10.728

22. Sample Obs 1 Obs 2 Obs 3 Obs 4 Obs 5 Avg Range
1 10.68 10.689 10.776 10.798 10.714 10.732 0.116
2 10.79 10.86 10.601 10.746 10.779 10.755 0.259
3 10.78 10.667 10.838 10.785 10.723 10.759 0.171
4 10.59 10.727 10.812 10.775 10.73 10.727 0.221
5 10.69 10.708 10.79 10.758 10.671 10.724 0.119
6 10.75 10.714 10.738 10.719 10.606 10.705 0.143
7 10.79 10.713 10.689 10.877 10.603 10.735 0.274
8 10.74 10.779 10.11 10.737 10.75 10.624 0.669
9 10.77 10.773 10.641 10.644 10.725 10.710 0.132
10 10.72 10.671 10.708 10.85 10.712 10.732 0.179
11 10.79 10.821 10.764 10.658 10.708 10.748 0.163
12 10.62 10.802 10.818 10.872 10.727 10.768 0.250
13 10.66 10.822 10.893 10.544 10.75 10.733 0.349
14 10.81 10.749 10.859 10.801 10.701 10.783 0.158
15 10.66 10.681 10.644 10.747 10.728 10.692 0.103
Averages 10.728 0.220400

23. x Chart Control Limits
UCL = x + A R
LCL = x - A R
2
2
R Chart Control Limits
UCL = D R
LCL = D R
4
3
n A2 D3 D4
2 1.88 0 3.27
3 1.02 0 2.57
4 0.73 0 2.28
5 0.58 0 2.11
6 0.48 0 2.00
7 0.42 0.08 1.92
8 0.37 0.14 1.86
9 0.34 0.18 1.82
10 0.31 0.22 1.78
11 0.29 0.26 1.74

24. Example of x-bar and R charts: Steps 3&4.
Calculate x-bar Chart and Plot Values
60110220405872810
85610220405872810
2
2
.)=.(-..R- AxLCL =
.)=.(..R+ AxUCL =


10.550
10.600
10.650
10.700
10.750
10.800
10.850
10.900
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Sample
Means
Sample
mean
UCL
LCL
grand
mean of x

25. Example of x-bar and R charts: Steps 5&6:
Calculate R-chart and Plot Values
0
0.46504


)2204.0)(0(RD=LCL
)2204.0)(11.2(RD=UCL
3
4
0.000
0.100
0.200
0.300
0.400
0.500
0.600
0.700
0.800
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Sample
R
Range
UCL
LCL
R-bar

26. P chart & c-chart

28. Constructing a P-Chart:
A Production manager for a tire company has
inspected the number of defective tires in five
random samples with 20 tires in each sample. The
table below shows the number of defective tires in
each sample of 20 tires.
Sample Sample
Size (n)
Number
Defective
1 20 3
2 20 2
3 20 1
4 20 2
5 20 1

29. Step 1:
Calculate the Percent defective of Each Sample
and the Overall Percent Defective (P-Bar)
Sample Number
Defective
Sample
Size
Percent
Defective
1 3 20 .15
2 2 20 .10
3 1 20 .05
4 2 20 .10
5 1 20 .05
Total 9 100 .09

30. Step 2: Calculate the Standard
Deviation of P
p
p(1-p) (.09)(.91)
σ = = =0.064
n 20

31. Step 3: Calculate CL, UCL, LCL
CL p .09 
 Center line (p bar):
 Control limits for ±3σ limits:
 
 
p
p
UCL p z σ .09 3(.064) .282
LCL p z σ .09 3(.064) .102 0
    
      

32. Step 4: Draw the Chart

33. Constructing a C-Chart:
The number of
weekly customer
complaints are
monitored in a
large hotel.
Develop a three
sigma control
limits For a C-
Chart using the
data table On
the right.
Week Number of
Complaints
1 3
2 2
3 3
4 1
5 3
6 3
7 2
8 1
9 3
10 1
Total 22

34. Calculate CL, UCL, LCL
 Center line (c bar):
 Control limits for ±3σ limits:
UCL c c 2.2 3 2.2 6.65
LCL c c 2.2 3 2.2 2.25 0
z
z
    
      
#complaints 22
CL 2.2
# of samples 10
  

35. Step 4: Draw the Chart