Downloaded 53 times
Uploaded byMital Damani
Sqcm
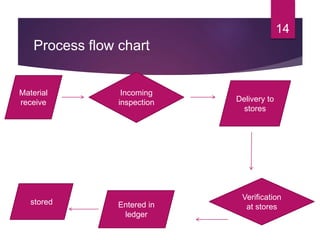
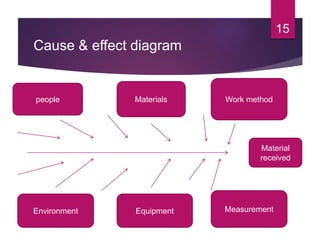
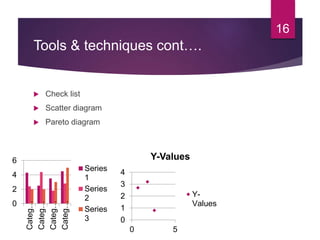
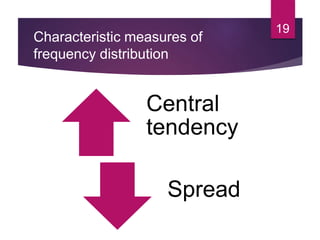
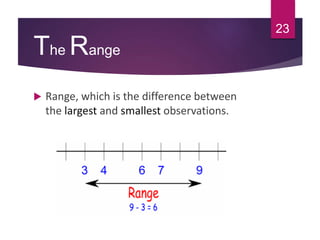
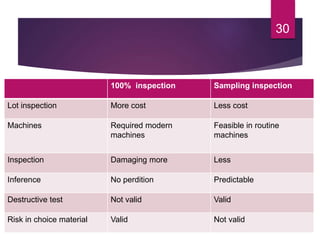
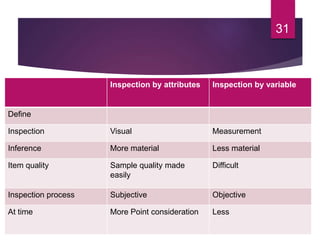
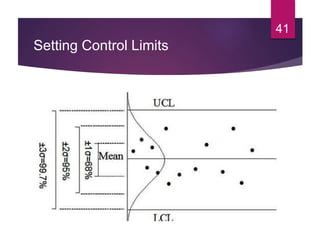
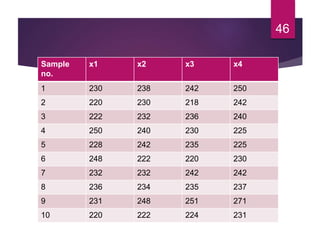
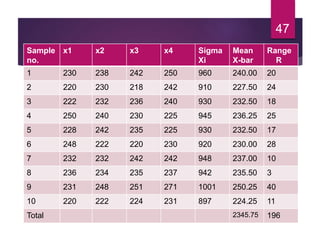
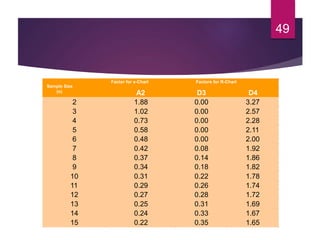
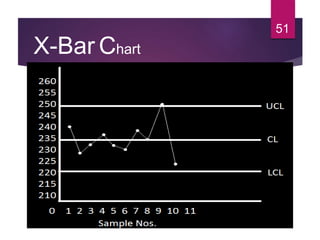
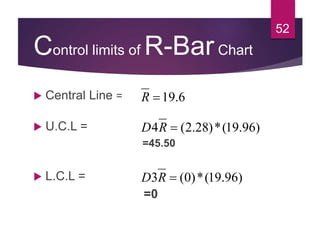
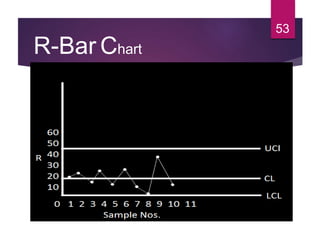
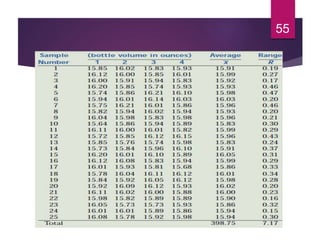
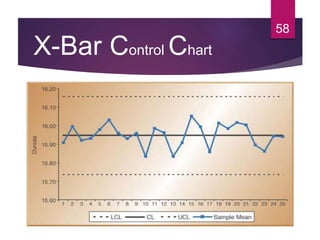
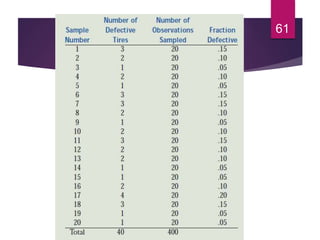
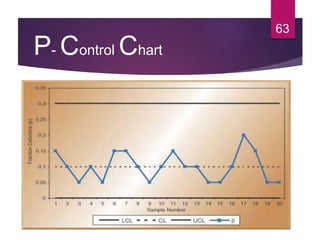
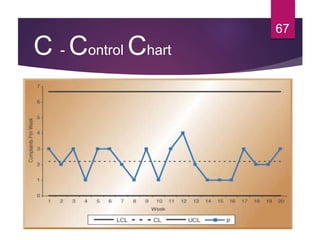
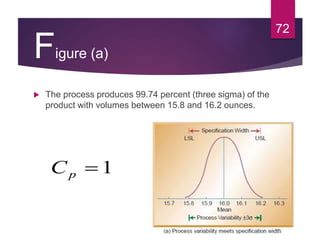
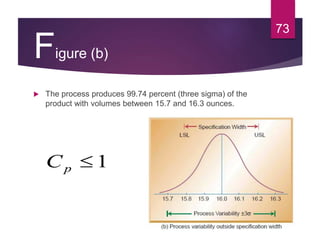
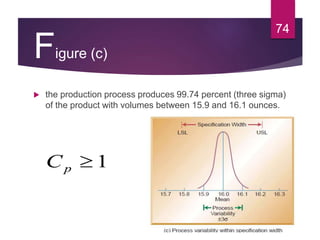
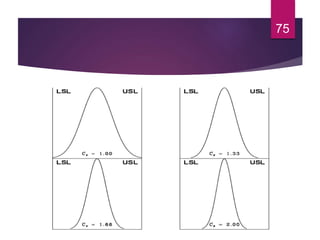
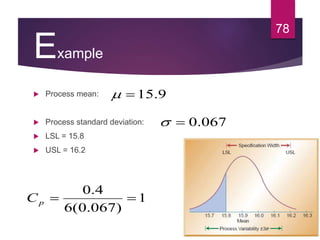
This document discusses statistical quality control and monitoring. It defines key terms like quality, quality control, statistical quality control, variables, attributes, and control limits. It describes the objectives of quality control as assuring reliability, durability, safety and meeting project requirements. Statistical process control tools like control charts, flow charts and sampling are explained. Common and assignable causes of variation are differentiated. Descriptive statistics used to characterize processes like mean, median, mode, variance and standard deviation are outlined. Control charts are identified as methods to monitor variables and attributes. Examples of X-bar and R charts are provided.
More Related Content
![Control Charts[1]](https://cdn.slidesharecdn.com/ss_thumbnails/controlcharts1-1226081330857138-9-thumbnail.jpg?width=640&height=640&fit=bounds)
Sqcm
- 1. Statistical Quality Control & Monitoring BY: ER.DAMANI MITAL. 1
- 2. What is Quality? Quality : Degree of excellence a product or service provides.. ..Like Design , execution , plumbing, masonry , elevation ,r.c.c , concrete, materials , many other s too .In short we can say quality mean each and every things which relate to our field and which going to use for construction or execution of all our idea in reality or practically in that good work and delivery of assurance should be in it . 2
- 3. Step to achievequality If we think for Low budget > Poor quality . The responsibility of quality is not only on builder but on project team , owner , consultant , contractor , supervisor , people , …all of us . The structure are good or not quality wise that assurance point is listed as follow : Architecture design & building design should be sound . Testing of structure on scale model should be carry out & result must be satisfactory . Use of material should be choice by its usage . Methodology , workmanship , team work , supervisor ….everybody must having sound knowledge 3
- 4. Quality control Q.Cdepend on workmanship , material , person , Type of project .. Etc Q.C is important part of project body but its important given to this point is too less …. In civil engineering the quality comprises of 3 things : Material used in construction Methodology used in project Testing of items 4
- 5. Factor affecting qualitycontrol Staff of Organization Methodology Skills of executive Supervisor standards Quality of raw material Quality control plan Machinery used for construction 5
- 6. Advantage of qualitycontrol Costing of project Wastage of material Less monitoring or inspection Firm reputation Technical knowledge became sound Complains from client reduced a lot speeding project get complete Override or penalty expenses reduced Machinery & staff complete in ideal time 6
- 7. Objectives of qualitycontrol Quality assurance :reliability ,durability , maintainability , interchange ability , safety , life of the structure Project completion must happen as Costing & valuation made for it The defect in project must be reduced The quality work should be as per decide by client and standard must be fulfilled If change I design wants from client then that should be done at a time of construction for good quality control The list of defect & problem happen while doing project must be noted down and that should be not repeated 7
- 8. Attributes & Variables Attributes : any physical changes Like temperature ,weight of material , size , measurement , etc …. Variables : abstraction belonging to entity or the assumption made to happen is not fulfllied Like Number of block in testing of conc cube , finishing of plaster , cracks in conc work , 8
- 9. What is SQC? Statistical quality control (SQC) is the term used to describe the set of statistical tools used by quality professionals. In the process of Q.C of material , method , testing material , … this all can be assured by standards and that is to be maintained through out project . Variables , attributes , unit & universe . 9
- 10. Advantage of S.Q.C Free from sources of variation By recognizing the fatal point and solve the things The safety of product increases inspection at different stages reduces Solve errors in Experimental Usage of scrap decrease a cost of production The notable changes in project seems good in development 10
- 11. Objectives of S.Q.C To notice the changes happens in quality and note down that for future use Take good step to improve a quality work Mark a goal to achieve a quality Reduced a wastage of material 11
- 12. Statistical process control The process use for monitoring a process of quality performance and its technics that what mean S.P.C Statistical : collecting , representation & analyzing data Process : a sequence of operations Control : measuring performance Objectives : - collect the feedback to improve work , find a source of problem created, predict about future step for improvement ,reduce weak point …. 12
- 13. Tools /Techniques forSPC Process flow chart Cause & effect diagram Check list Scatter diagram Pareto diagram Histogram Control charts Sampling 13
- 14. Process flow chart 14 Material receive Incoming inspectionDelivery to stores Verification at storesEntered in ledger stored
- 15. Cause & effectdiagram 15 people Materials Work method Material received MeasurementEquipmentEnvironment
- 16. Tools & techniquescont…. Check list Scatter diagram Pareto diagram 16 0 1 2 3 4 0 5 Y-Values Y- Values0 2 4 6 Categ… Categ… Categ… Categ… Series 1 Series 2 Series 3
- 17. Methods of statisticalquality control (S.Q.C) Frequency distribution Control chart Acceptance sampling Special methods 17
- 18.
- 19. Characteristic measures of frequencydistribution 19 Central tendency Spread
- 20. Descriptive Statistics Descriptivestatistics are used to describe quality characteristics and relationships. 20
- 21. Descriptive Statistics TheMean- measure of central tendency Median - the mid numeric Mode - the variable whose numeric value is highest Variance - the difference of single numeric and summation of numeric Co-efficient of variance The Range- difference between largest/smallest observations in a set of data Standard Deviation measures the amount of data dispersion around mean 21
- 22. The Mean Tocompute the mean we simply sum all the observations and divide by the total no. of observations. 22
- 23. The Range Range,which is the difference between the largest and smallest observations. 23
- 24. Variance V= (x– ŦŦ ) x = numeric value Ŧ = summation of value V = Variance Co – efficient of variance :- C= s/x x10 Range :- R = xmax – xmin 24
- 25. Standard Deviation Standarddeviation is a measure of dispersion of a curve. It measures the extent to which these values are scattered around the central mean. 25
- 26. • Extend theuse of descriptive statistics to monitor the quality of the product and process • Statistical process control help to determine the amount of variation • To make sure the process is in a state of control Statistical process control 26 26
- 27. Variation in Quality No two items are exactly alike. Some sort of variations in the two items is bound to be there. In fact it is an integral part of any manufacturing process. This difference in characteristics known as variation. This variation may be due to substandard quality of raw material, carelessness on the part of operator, fault in machinery system etc.. 27
- 28. Important terms Sample Sample size Sampling fraction Item Sampling Lot Lot size Inspection 28
- 29. Sampling techniques Simple randomsampling Stratified sampling Systematic sampling Cluster sampling Two stage sampling Refer book content …. 29
- 30. 30 100% inspection Samplinginspection Lot inspection More cost Less cost Machines Required modern machines Feasible in routine machines Inspection Damaging more Less Inference No perdition Predictable Destructive test Not valid Valid Risk in choice material Valid Not valid
- 31. Inspection by attributesInspection by variable Define Inspection Visual Measurement Inference More material Less material Item quality Sample quality made easily Difficult Inspection process Subjective Objective At time More Point consideration Less 31
- 32. Acceptance sampling Dividingwhole lot into small part Take a random sample from lot Inspect that sample and come to result Based on inspection result take decision to accept or reject the lot 32
- 33. Pros & Nrosof acceptance sampling Low costing in inspection process Easy & feasible This method is convent for big lot Less stressful Time consuming is less Decrease the chance of lot acceptance by supplier Supplier may accept Poor quality of lot 33
- 34. Sampling plan Single sampleplan Double sample plan Multiple sampling plan Sequential sampling plan 34
- 35. Symbol used forsampling plan calculation N = total number of product n = sample number C = acceptance number r = rejected number For eg : n= 7 N= 100 C=0 35
- 36.
- 37. Variation due tochance causes/common causes Variation occurred due to chance. This variation is NOT due to defect in machine, Raw material or any other factors. Behave in “random manner”. Negligible but Inevitable The process is said to be under the state of statistical control. 3737
- 38. Variation due toassignable causes Non – random causes like: Difference in quality of raw material Difference in machines Difference in operators Difference of time 38 38
- 39.
- 40. Specification and controllimits No item in the world can be a true copy of another item. It is not expressed in absolute values but in terms of a range. For Eg: The diameter of a pen is expected by its manufacturer not as 7mm but as 7mm ± 0.05. Thus, the diameter of a pen produced by the manufacturer can vary from 6.95 mm to 7.05 mm. 40
- 41.
- 42. HOW CONTROL LIMITSARE USEFUL…..? 42
- 43. SPC Methods-Control Charts Control Charts show sample data plotted on a graph with CL, UCL, and LCL Control chart for variables are used to monitor characteristics that can be measured, e.g. length, weight, diameter, time Control charts for attributes are used to monitor characteristics that have discrete values and can be counted, e.g. % defective, number of flaws in a shirt, number of broken eggs in a box 43
- 44. Control Charts forVariables x-bar charts It is used to monitor the changes in the mean of a process (central tendencies). R-bar charts It is used to monitor the dispersion or variability of the process 44
- 45. Constructing a X-barchart ( sigma is not given) A factory produces 50 cylinders per hour. Samples of 10 cylinders are taken at random from the production at every hour and the diameters of cylinders are measured. Draw X-bar and R charts and decide whether the process is under control or not. (For n=4 A2= 0.73 D3= 0, D4=2.28) 45
- 46. Sample no. x1 x2 x3x4 1 230 238 242 250 2 220 230 218 242 3 222 232 236 240 4 250 240 230 225 5 228 242 235 225 6 248 222 220 230 7 232 232 242 242 8 236 234 235 237 9 231 248 251 271 10 220 222 224 231 46
- 47. Sample no. x1 x2 x3x4 Sigma Xi Mean X-bar Range R 1 230 238 242 250 960 240.00 20 2 220 230 218 242 910 227.50 24 3 222 232 236 240 930 232.50 18 4 250 240 230 225 945 236.25 25 5 228 242 235 225 930 232.50 17 6 248 222 220 230 920 230.00 28 7 232 232 242 242 948 237.00 10 8 236 234 235 237 942 235.50 3 9 231 248 251 271 1001 250.25 40 10 220 222 224 231 897 224.25 11 Total 2345.75 196 47
- 48. Calculation of x-barand R-bar Now, 75.234 10 75.2345 m x x 6.19 10 196 m R R 48
- 49. 49 Factor for x-Chart A2D3 D4 2 1.88 0.00 3.27 3 1.02 0.00 2.57 4 0.73 0.00 2.28 5 0.58 0.00 2.11 6 0.48 0.00 2.00 7 0.42 0.08 1.92 8 0.37 0.14 1.86 9 0.34 0.18 1.82 10 0.31 0.22 1.78 11 0.29 0.26 1.74 12 0.27 0.28 1.72 13 0.25 0.31 1.69 14 0.24 0.33 1.67 15 0.22 0.35 1.65 Factors for R-Chart Sample Size (n)
- 50. Control limits ofX-BarChart Central line C.L = U.C.L = =234.75 + (0.73) (19.6) =249.06 L.C.L= =234.75- (0.73) (19.6) =220.72 RAx *2 RAx *2 75.234x 50
- 51.
- 52. Control limits ofR-BarChart Central Line = U.C.L = =45.50 L.C.L = =0 6.19R )96.19(*)28.2(4 RD )96.19(*)0(3 RD 52
- 53.
- 54. Constructing a X-barChart (Sigma is given) A quality control inspector at the Coca-Cola soft drink company has taken twenty-five samples with four observations each of the volume of bottles filled. The data and the computed means are shown in the table. If the standard deviation of the bottling operation is 0.14 ounces, use this information to develop control limits of three standard deviations for the bottling operation. 54
- 55.
- 56.
- 57.
- 58.
- 59. Control Charts forAttributes Attributes are discrete events; yes/no, pass/fail Use P-Charts for quality characteristics that are discrete and involve yes/no or good/bad decisions Number of leaking caulking tubes in a box of 48 Number of broken eggs in a carton Use C-Charts for discrete defects when there can be more than one defect per unit Number of flaws or stains in a carpet sample cut from a production run Number of complaints per customer at a hotel 59
- 60. P-Chart Example AProduction manager of a BKT tire company has inspected the number of defective tires in five random samples with 20 tires in each sample. The table below shows the number of defective tires in each sample of 20 tires. Calculate the control limits. 60
- 61.
- 62.
- 63.
- 64. C - ChartExample The number of weekly customer complaints are monitored in a large hotel using a c-chart. Develop three sigma control limits using the data table below. 64
- 65.
- 66.
- 67. C - ControlChart 67
- 68. Process Capability Evaluatingthe ability of a production process to meet or exceed preset specifications. This is called process capability. Product specifications, often called tolerances, are preset ranges of acceptable quality characteristics, such as product dimensions. 68
- 69. Two parts ofprocess capability 1) Measure the variability of the output of a process, and 2) Compare that variability with a proposed specification or product tolerance. 69
- 70. Measuring Process Capability To produce an acceptable product, the process must be capable and in control before production begins. 70 6 LSLUSL Cp
- 71. Example Let’s saythat the specification for the acceptable volume of liquid is preset at 16 ounces ±.2 ounces, which is 15.8 and 16.2 ounces. 71
- 72. Figure (a) Theprocess produces 99.74 percent (three sigma) of the product with volumes between 15.8 and 16.2 ounces. 72 1pC
- 73. Figure (b) Theprocess produces 99.74 percent (three sigma) of the product with volumes between 15.7 and 16.3 ounces. 73 1pC
- 74. Figure (c) theproduction process produces 99.74 percent (three sigma) of the product with volumes between 15.9 and 16.1 ounces. 74 1pC
- 75.
- 76.
- 77. Process capability ratio (offcentering process) There is a possibility that the process mean may shift over a period of time, in either direction, i.e., towards the USL or the LSL. This may result in more defective items then the expected. This shift of the process mean is called the off-centering of the process. 77 3 , 3 min LSLUSL C kp
- 78. Example 78 Process mean: Process standard deviation: LSL = 15.8 USL = 16.2 9.15 067.0 1 )067.0(6 4.0 pC
- 79.
- 80.