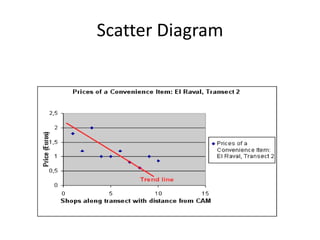
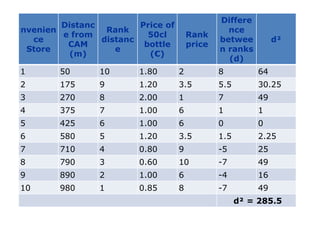
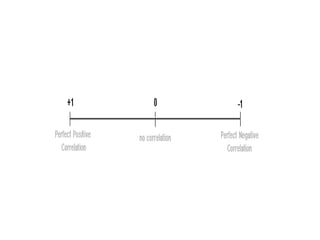
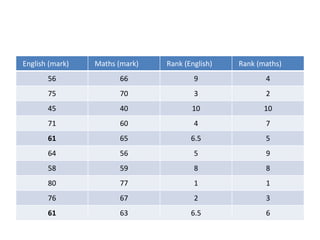
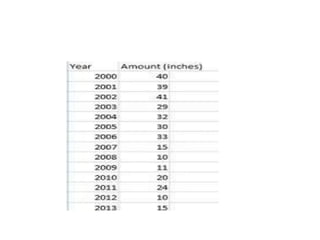
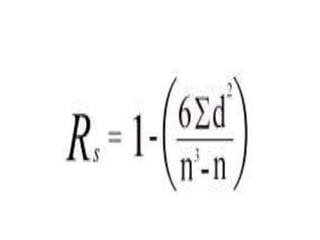Spearman's rank correlation coefficient is used to measure the strength of association between two ranked variables. It involves ranking the data values and calculating the differences between the ranks to determine if there is a monotonic relationship between the variables. The coefficient value ranges from +1 to -1, where +1 is a perfect increasing monotonic relationship and -1 is a perfect decreasing relationship. The example calculates the Spearman's rank correlation coefficient between the distance of convenience stores from a museum and the price of water bottles sold. It finds the ranks of the distances and prices, takes the differences of the ranks, sums the squared differences, and plugs the values into the Spearman's rank correlation formula to determine the coefficient value.

1. Spearman's Rank Correlation
Coefficient
- Dr. Karishma Chaudhary

2. • The Spearman's Rank Correlation Coefficient is
used to discover the strength of a link
between two sets of data.
• This example looks at the strength of the link
between the price of a convenience item (a
50cl bottle of water) and distance from the
Contemporary Art Museum.

3. Step 1
• Data collection

4. Scatter Diagram

5. • Calculate the coefficient (Rs) using the formula
below. The answer will always be between 1.0
(a perfect positive correlation) and -1.0 (a
perfect negative correlation).
•
When written in mathematical notation the
Spearman Rank formula looks like this :

6. Method - calculating the coefficient
• Create a table from your data.
• Rank the two data sets. Ranking is achieved by giving the ranking '1' to the
biggest number in a column, '2' to the second biggest value and so on. The
smallest value in the column will get the lowest ranking. This should be
done for both sets of measurements.
• Tied scores are given the mean (average) rank. For example, the three tied
scores of 1 euro in the example below are ranked fifth in order of price,
but occupy three positions (fifth, sixth and seventh) in a ranking hierarchy
of ten. The mean rank in this case is calculated as (5+6+7) ÷ 3 = 6.
• Find the difference in the ranks (d): This is the difference between the
ranks of the two values on each row of the table. The rank of the second
value (price) is subtracted from the rank of the first (distance from the
museum).
• Square the differences (d²) To remove negative values and then sum them
(d²).

8. nvenien
ce
Store
Distanc
e from
CAM
(m)
Rank
distanc
e
Price of
50cl
bottle
(€)
Rank
price
Differe
nce
betwee
n ranks
(d)
d²
1 50 10 1.80 2 8 64
2 175 9 1.20 3.5 5.5 30.25
3 270 8 2.00 1 7 49
4 375 7 1.00 6 1 1
5 425 6 1.00 6 0 0
6 580 5 1.20 3.5 1.5 2.25
7 710 4 0.80 9 -5 25
8 790 3 0.60 10 -7 49
9 890 2 1.00 6 -4 16
10 980 1 0.85 8 -7 49
d² = 285.5

9. • Now to put all these values into the formula.
• Find the value of all the d² values by adding up all the
values in the Difference² column. In our example this
is 285.5. Multiplying this by 6 gives 1713.
• Now for the bottom line of the equation. The value n is
the number of sites at which you took measurements.
This, in our example is 10. Substituting these values
into n³ - n we get 1000 - 10
• We now have the formula: Rs = 1 - (1713/990) which
gives a value for Rs:1 - 1.73 = -0.73

10. • The closer Rs is to +1 or -1, the stronger the
likely correlation. A perfect positive
correlation is +1 and a perfect negative
correlation is -1. The Rs value of -0.73 suggests
a fairly strong negative relationship

12. Find the Spearman's rank-order
correlation
Marks
Eng
lish
56 75 45 71 61 64 58 80 76 61
Ma
ths
66 70 40 60 65 56 59 77 67 63

13. English (mark) Maths (mark) Rank (English) Rank (maths)
56 66 9 4
75 70 3 2
45 40 10 10
71 60 4 7
61 65 6.5 5
64 56 5 9
58 59 8 8
80 77 1 1
76 67 2 3
61 63 6.5 6

14. Regression Analysis: An Introduction
• In statistics, it’s hard to stare at a set of random
numbers in a table and try to make any sense of
it. For example, global warming may be
reducing average snowfall in your town and you
are asked to predict how much snow you think
will fall this year. Looking at the following table
you might guess somewhere around 10-20
inches. That’s a good guess, but you could make
a better guess, by using regression.