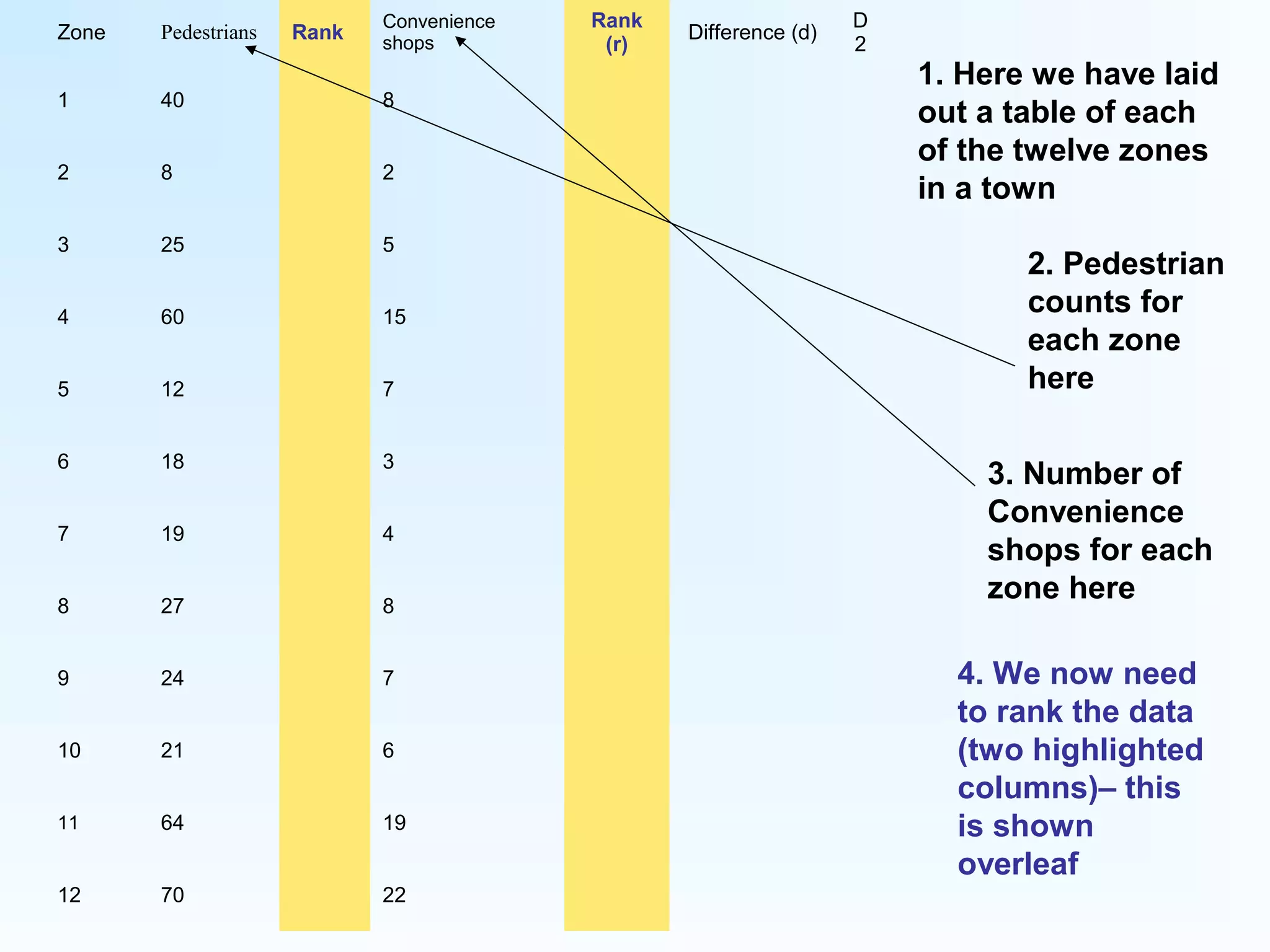
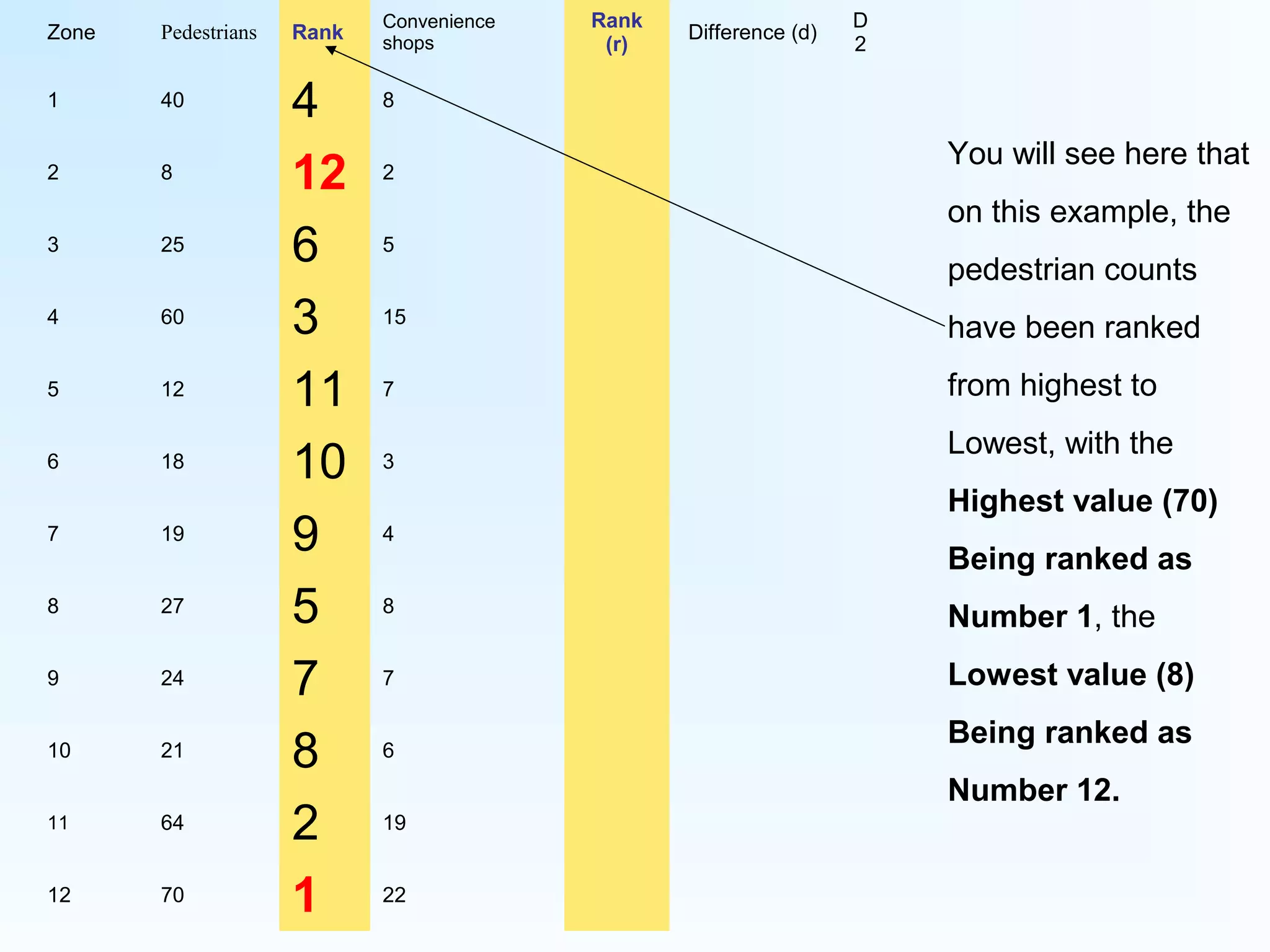
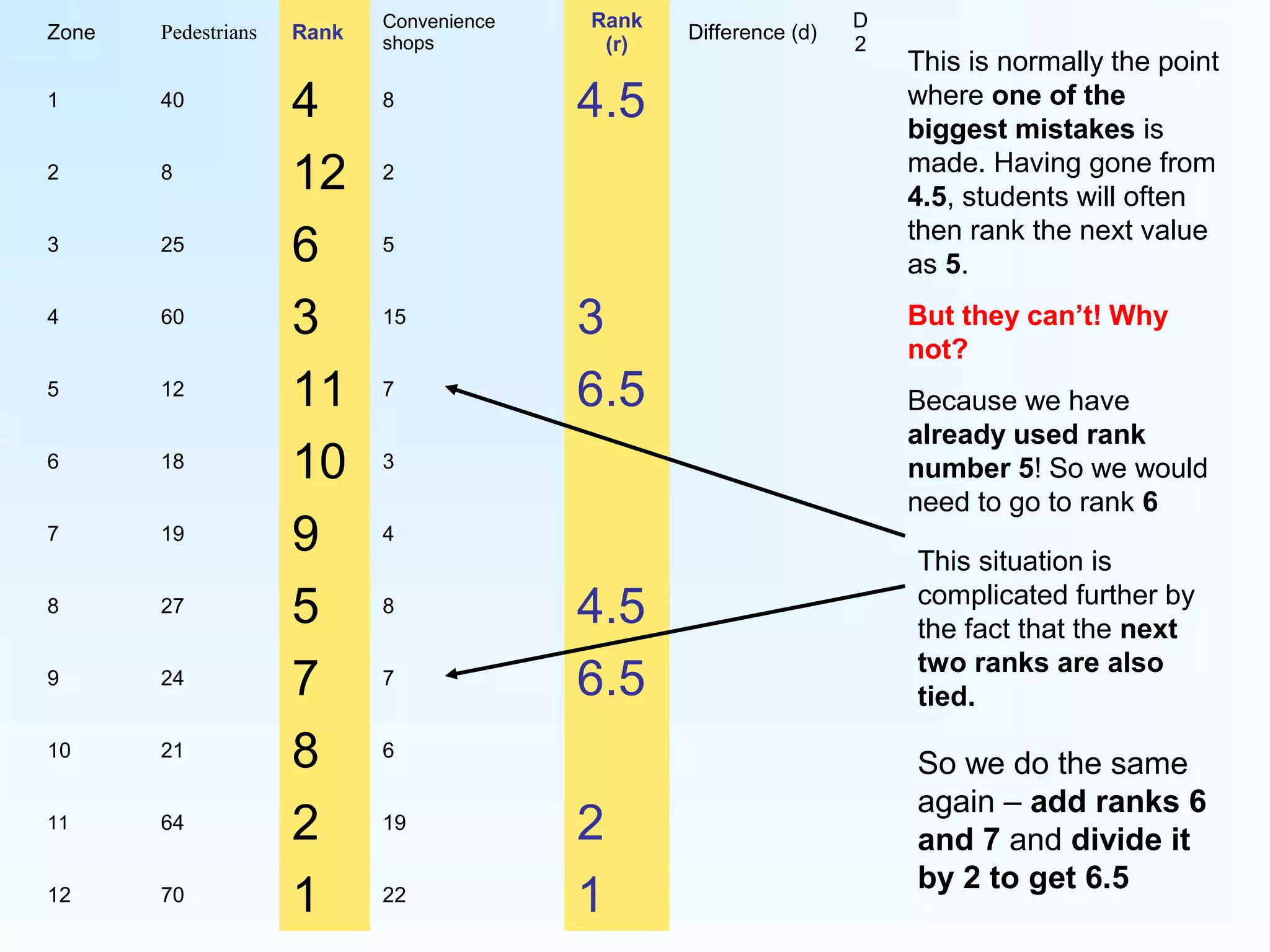
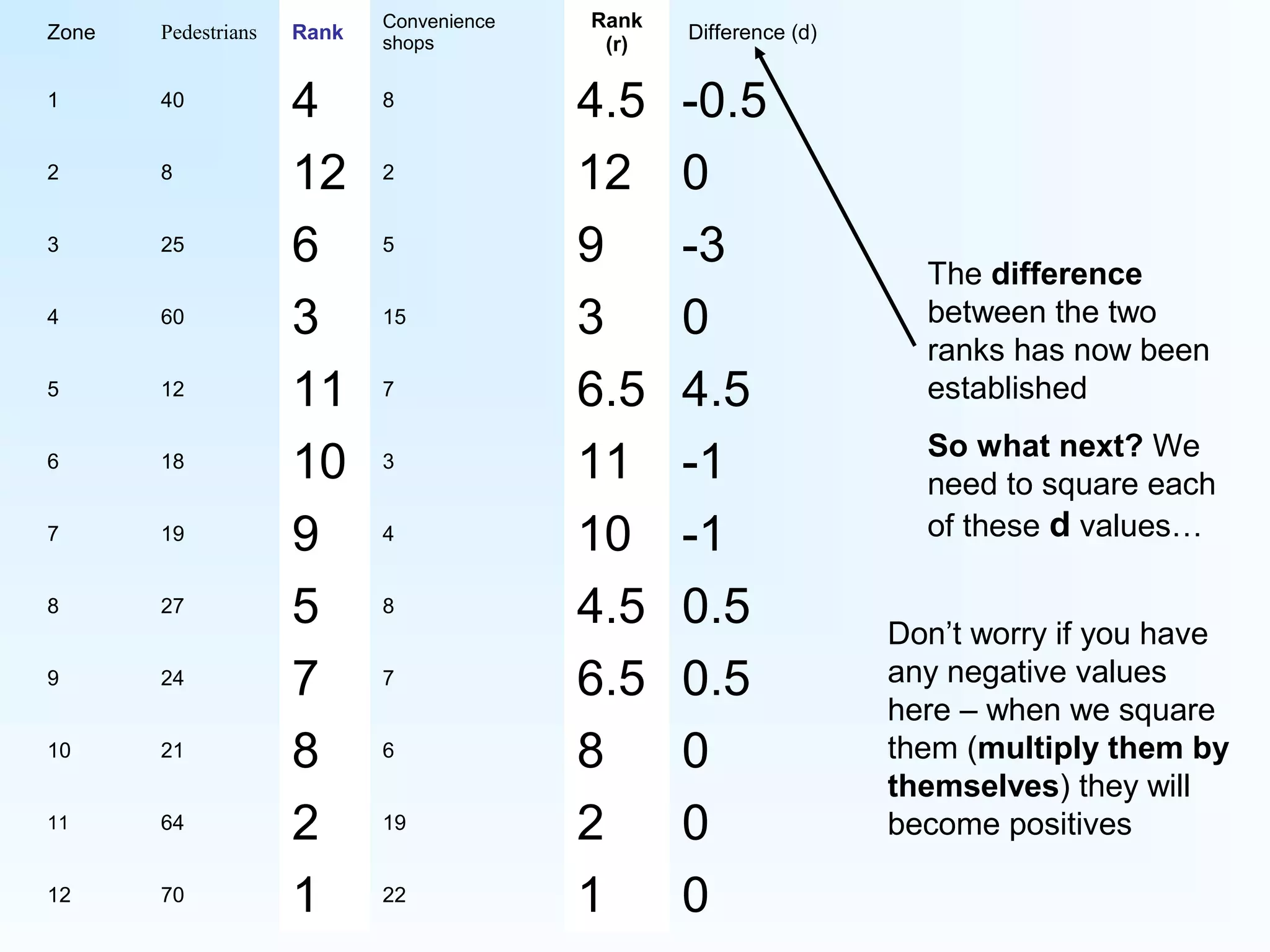
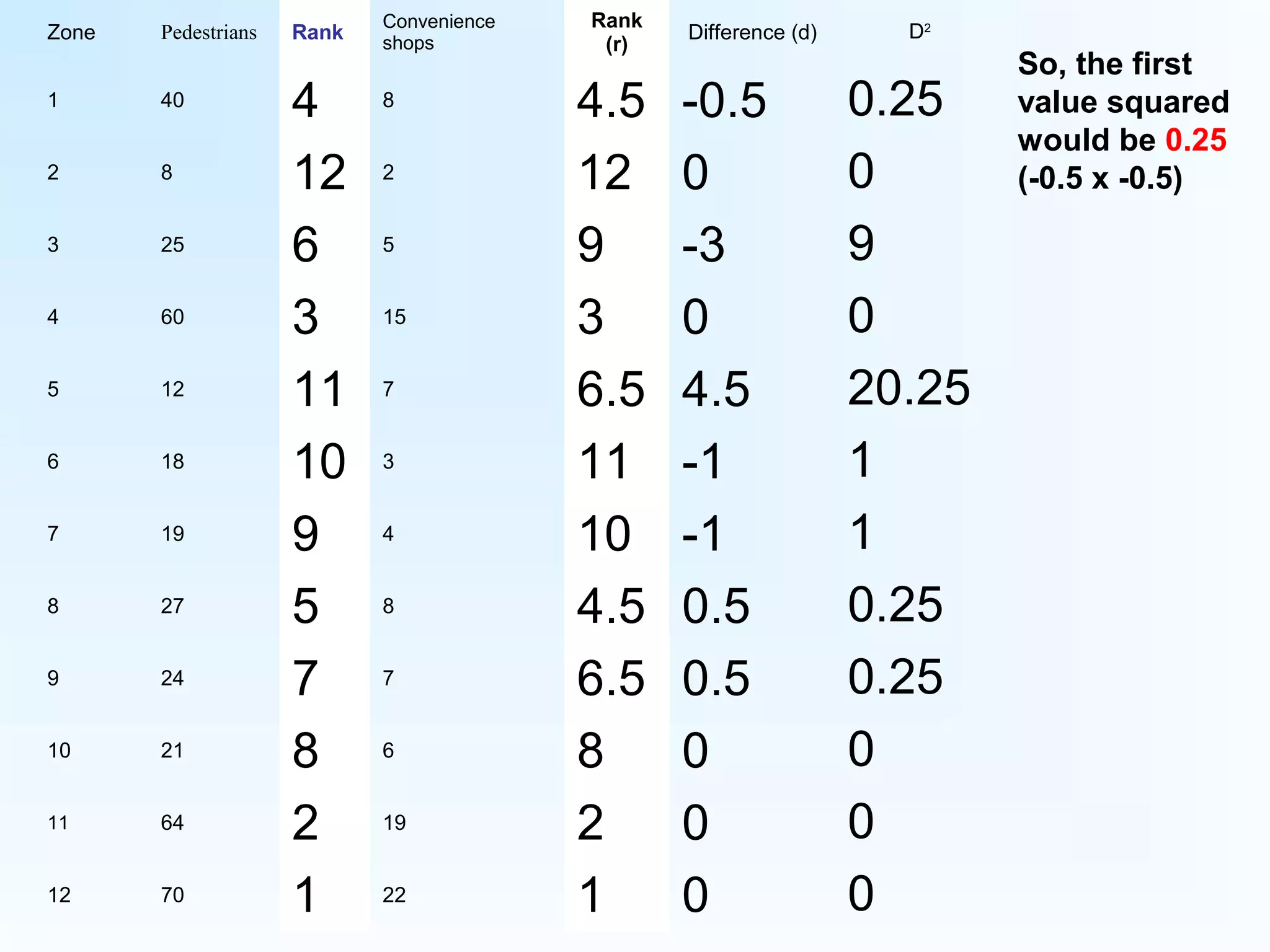
This document provides instructions for calculating and interpreting Spearman's rank correlation coefficient. It begins with an example comparing pedestrian counts and convenience shops in 12 town zones. Tables are constructed to rank the data and calculate differences between ranks. The equation for Spearman's rank is shown and applied to the example data, yielding a value of 0.888. This indicates a fairly positive relationship between pedestrian counts and shops. Critical values tables are presented to determine statistical significance based on the sample size. In this case, the value exceeds thresholds for 95% and 99% confidence, showing a highly significant relationship.

1. How and why to use
Spearman’s Rank…
If you have done scattergraphs,
Spearman’s Rank offers you the
opportunity to use a statistical test
to get a value which can determine
the strength of the relationship
between two sets of data…

2. So how do we do it?
This is the equation, and looks complicated,
so let’s think carefully about how we can do
this…
The best way to do this would be through an example.
If we were looking at Settlement patterns for a town’s CBD in
Geography, we may wish to compare aspects of the town,
such as whether the number of people in a zone affect the type
of shops that locate there (i.e. – convenience shops)
To do this, we would construct a table as shown overleaf…
In the above, rs refers to the overall value or rank
The equation has to be done before the value is taken away from 1
In the above equation, the sign means ‘the total of’
d2
is the first thing we will try to establish in our ranked tables (see next
slides)
‘n’ refers to the number of sites or values you will process – so if there
were there 15 river sites, ‘n’ would be 15. If there were 20 pedestrian
count zones, ‘n’ would be 20, and so on…

3. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
D
2
1 40 8
2 8 2
3 25 5
4 60 15
5 12 7
6 18 3
7 19 4
8 27 8
9 24 7
10 21 6
11 64 19
12 70 22
1. Here we have laid
out a table of each
of the twelve zones
in a town
2. Pedestrian
counts for
each zone
here
3. Number of
Convenience
shops for each
zone here
4. We now need
to rank the data
(two highlighted
columns)– this
is shown
overleaf

4. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
D
2
1 40 4 8
2 8 12 2
3 25 6 5
4 60 3 15
5 12 11 7
6 18 10 3
7 19 9 4
8 27 5 8
9 24 7 7
10 21 8 6
11 64 2 19
12 70 1 22
You will see here that
on this example, the
pedestrian counts
have been ranked
from highest to
Lowest, with the
Highest value (70)
Being ranked as
Number 1, the
Lowest value (8)
Being ranked as
Number 12.

5. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
D
2
1 40 4 8
2 8 12 2
3 25 6 5
4 60 3 15 3
5 12 11 7
6 18 10 3
7 19 9 4
8 27 5 8
9 24 7 7
10 21 8 6
11 64 2 19 2
12 70 1 22 1
So that was fairly easy…
We need to now do the
next column for
Convenience shops too.
But hang on!
Now we have a
problem…
We have two values
that are 8, so what do
we do?
The next two ranks
would be 4 and 5; we
add the two ranks
together and divide it by
two. So these two ranks
would both be called 4.5

6. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
D
2
1 40 4 8 4.5
2 8 12 2
3 25 6 5
4 60 3 15 3
5 12 11 7 6.5
6 18 10 3
7 19 9 4
8 27 5 8 4.5
9 24 7 7 6.5
10 21 8 6
11 64 2 19 2
12 70 1 22 1
This is normally the point
where one of the
biggest mistakes is
made. Having gone from
4.5, students will often
then rank the next value
as 5.
But they can’t! Why
not?
Because we have
already used rank
number 5! So we would
need to go to rank 6
This situation is
complicated further by
the fact that the next
two ranks are also
tied.
So we do the same
again – add ranks 6
and 7 and divide it
by 2 to get 6.5

7. Rank
Rank
(r)
4 4.5
12 12
6 9
3 3
11 6.5
10 11
9 10
5 4.5
7 6.5
8 8
2 2
1 1
Having ranked both sets
of data we now need to
work out the difference
(d) between the two
ranks. To do this we
would take the second
rank away from the
first.
This is demonstrated
on the next slide

8. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
1 40 4 8 4.5 -0.5
2 8 12 2 12 0
3 25 6 5 9 -3
4 60 3 15 3 0
5 12 11 7 6.5 4.5
6 18 10 3 11 -1
7 19 9 4 10 -1
8 27 5 8 4.5 0.5
9 24 7 7 6.5 0.5
10 21 8 6 8 0
11 64 2 19 2 0
12 70 1 22 1 0
The difference
between the two
ranks has now been
established
So what next? We
need to square each
of these d values…
Don’t worry if you have
any negative values
here – when we square
them (multiply them by
themselves) they will
become positives

9. Zone Pedestrians Rank
Convenience
shops
Rank
(r)
Difference (d)
1 40 4 8 4.5 -0.5
2 8 12 2 12 0
3 25 6 5 9 -3
4 60 3 15 3 0
5 12 11 7 6.5 4.5
6 18 10 3 11 -1
7 19 9 4 10 -1
8 27 5 8 4.5 0.5
9 24 7 7 6.5 0.5
10 21 8 6 8 0
11 64 2 19 2 0
12 70 1 22 1 0
D2
0.25
0
9
0
20.25
1
1
0.25
0.25
0
0
0
So, the first
value squared
would be 0.25
(-0.5 x -0.5)

10. So what do we with these ‘d2
’
figures?
First we need to add all of the figures in this d2
column
together
This gives us…. 32
Now we can think about
doing the actual equation!

11. Firstly, let’s remind ourselves of the equation...
In this equation, we know the total of d2
, which is 32
So the top part of our equation is…
6 x 32
We also know what ‘n’ is (the number of sites or
zones - 12 in this case), so the bottom part of the
equation is…
(12x12x12) - 12

12. We can now do the equation…
6 x 32
123
- 12
192
1716
OK – so this gives us a figure
of 0.111888111888

13. This is the equation, which we will by now
be sick of!
I have circled the part of the equation that we have done…
Remember that we need to take this value that we have calculated away
from 1. Forgetting to do this is probably the second biggest mistake
that people make!
So…
1 – 0. 111888111888 = 0.888

14. So we have our Spearman’s Rank
figure….But what does it mean?
-1 0 +1
0.888
Your value will always be between -1 and +1 in value. As a rough guide, our
figure of 0.888 demonstrates there is a fairly positive relationship. It suggests that
where pedestrian counts are high, there are a high number of convenience shops
Should the figure be close to -1, it would suggest that there is a negative
relationship, and that as one thing increases, the other decreases.

15. However…
Just looking at a line and making an
estimation isn’t particularly
scientific. To be more sure, we need
to look in critical values tables to
see the level of significance and
strength of the relationship. This is
shown overleaf…

16. N
0.05
level 0.01 level
12 0.591 0.777
14 0.544 0.715
16 0.506 0.665
18 0.475 0.625
20 0.45 0.591
22 0.428 0.562
24 0.409 0.537
26 0.392 0.515
28 0.377 0.496
30 0.364 0.478
1. This is a critical values table and the
‘n’ column shows the numbers of sites
or zones you have studied. In our case,
we looked at 12 zones.
2. If look across we can see there are
two further columns – one labelled 0.05,
the other 0.01.
The first, 0.05 means that if our figure
exceeds the value, we can be sure that
95 times in 100 the figures occurred
because a relationship exists, and not
because of pure chance
The second, 0.01, means that if our
figure exceeds this value, we can be
sure that 99 times in 100 the figures
occcurred because a relationship exists,
and did not occur by chance.
We can see that in our
example our figure of 0.888
exceeds the value of 0.591 at
the 0.05 level and also
comfortably exceeds value at
the 0.01 level too.

17. In our example above, we can see
that our figure of 0.888 exceeds the
values at both the 95% and 99%
levels. The figure is therefore highly
significant

18. Finally…
You need to think how you can use this
yourself…I would advise that you do
scattergraphs for the same sets of data so
that you have a direct comparison